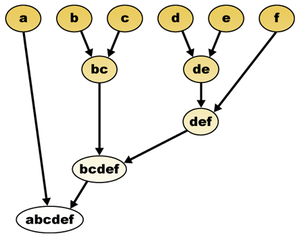
Algorytm łańcucha najbliższego sąsiada

W teorii analizy skupień algorytm łańcucha najbliższego sąsiada to algorytm , który może przyspieszyć kilka metod aglomeracyjnego hierarchicznego grupowania . Są to metody, które przyjmują zbiór punktów jako dane wejściowe i tworzą hierarchię klastrów punktów poprzez wielokrotne łączenie par mniejszych klastrów w celu utworzenia większych klastrów. Metody grupowania, do których można zastosować algorytm łańcucha najbliższego sąsiedztwa, obejmują metodę Warda , klastrowanie z pełnym powiązaniem i klastrowanie z pojedynczym powiązaniem ; wszystkie one działają poprzez wielokrotne łączenie dwóch najbliższych klastrów, ale używają różnych definicji odległości między klastrami. Odległości klastrów, dla których działa algorytm łańcucha najbliższego sąsiedztwa, nazywane są redukowalnymi i charakteryzują się prostą nierównością między pewnymi odległościami klastrów.

Główną ideą algorytmu jest znalezienie par klastrów do połączenia poprzez podążanie ścieżkami w grafie najbliższego sąsiada klastrów. Każda taka ścieżka ostatecznie zakończy się na parze klastrów, które są najbliższymi sąsiadami względem siebie, a algorytm wybiera tę parę klastrów jako parę do połączenia. W celu zaoszczędzenia pracy poprzez ponowne wykorzystanie jak największej ilości każdej ścieżki, algorytm wykorzystuje strukturę danych stosu aby śledzić każdą ścieżkę, którą podąża. Podążając ścieżkami w ten sposób, algorytm łańcucha najbliższego sąsiada łączy swoje klastry w innej kolejności niż metody, które zawsze znajdują i scalają najbliższą parę klastrów. Jednak pomimo tej różnicy zawsze generuje tę samą hierarchię klastrów.

Algorytm łańcucha najbliższego sąsiada konstruuje grupowanie w czasie proporcjonalnym do kwadratu liczby punktów, które mają być skupione. Jest to również proporcjonalne do wielkości jego danych wejściowych, gdy dane wejściowe są dostarczane w postaci wyraźnej macierzy odległości . Algorytm wykorzystuje ilość pamięci proporcjonalną do liczby punktów, gdy jest używany do grupowania metod, takich jak metoda Warda, która umożliwia obliczanie odległości między klastrami w czasie stałym. Jednak w przypadku niektórych innych metod grupowania wykorzystuje większą ilość pamięci w pomocniczej strukturze danych, za pomocą której śledzi odległości między parami klastrów.

Tło

Hierarchiczne skupienie sześciu punktów. Punkty, które mają być skupione, znajdują się na górze diagramu, a węzły poniżej reprezentują skupienia.

Wiele problemów w analizie danych dotyczy grupowania , grupowania elementów danych w klastry blisko powiązanych elementów. Grupowanie hierarchiczne to wersja analizy skupień, w której klastry tworzą hierarchię lub strukturę przypominającą drzewo, a nie ścisły podział elementów danych. W niektórych przypadkach ten typ grupowania może być wykonywany jako sposób przeprowadzania analizy skupień w wielu różnych skalach jednocześnie. W innych przypadkach dane do analizy mają naturalnie nieznaną strukturę drzewa, a celem jest odzyskanie tej struktury poprzez wykonanie analizy. Oba te rodzaje analiz można zobaczyć na przykład w zastosowaniu hierarchicznego grupowania do taksonomii biologicznej . W tej aplikacji różne żywe istoty są pogrupowane w klastry o różnych skalach lub poziomach podobieństwa ( gatunek, rodzaj, rodzina itp. ). Ta analiza jednocześnie daje wieloskalowe grupowanie organizmów obecnej epoki i ma na celu dokładną rekonstrukcję procesu rozgałęziania lub drzewa ewolucyjnego , które w minionych wiekach wytworzyło te organizmy.

Dane wejściowe do problemu grupowania składają się z zestawu punktów. Klaster to dowolny właściwy podzbiór punktów, a grupowanie hierarchiczne to maksymalna rodzina klastrów z tą właściwością, że dowolne dwa klastry w rodzinie są albo zagnieżdżone, albo rozłączne . Alternatywnie, hierarchiczne grupowanie może być reprezentowane jako drzewo binarne z punktami na jego liściach; klastry klastrowania to zbiory punktów w poddrzewach wychodzących z każdego węzła drzewa.

W metodach grupowania aglomeracyjnego dane wejściowe obejmują również funkcję odległości zdefiniowaną na punktach lub liczbową miarę ich odmienności. Odległość lub odmienność powinna być symetryczna: odległość między dwoma punktami nie zależy od tego, który z nich jest rozpatrywany jako pierwszy. Jednak w przeciwieństwie do odległości w przestrzeni metrycznej nie jest wymagane spełnienie nierówności trójkąta . Następnie funkcja odmienności jest rozszerzana z par punktów na pary klastrów. Różne metody grupowania wykonują to rozszerzenie na różne sposoby. Na przykład w klastrowaniu z pojedynczym powiązaniem W metodzie odległość między dwoma skupieniami jest definiowana jako minimalna odległość między dowolnymi dwoma punktami z każdego skupienia. Biorąc pod uwagę tę odległość między klastrami, klastry hierarchiczne można zdefiniować za pomocą zachłannego algorytmu , który początkowo umieszcza każdy punkt we własnym klastrze jednopunktowym, a następnie wielokrotnie tworzy nowy klaster, łącząc najbliższe pary klastrów.

Wąskim gardłem tego zachłannego algorytmu jest podproblem znalezienia dwóch klastrów do połączenia w każdym kroku. Znane metody wielokrotnego znajdowania najbliższej pary klastrów w dynamicznym zestawie klastrów albo wymagają przestrzeni nadliniowej do utrzymania struktury danych które mogą szybko znaleźć najbliższe pary lub znalezienie każdej najbliższej pary zajmuje więcej niż czas liniowy. Algorytm łańcucha najbliższego sąsiada wykorzystuje mniejszą ilość czasu i przestrzeni niż algorytm zachłanny, łącząc pary klastrów w innej kolejności. W ten sposób unika się problemu wielokrotnego znajdowania najbliższych par. Niemniej jednak w przypadku wielu typów problemów z grupowaniem można zagwarantować, że otrzyma to samo hierarchiczne grupowanie, co algorytm zachłanny, pomimo innej kolejności scalania.

Algorytm

Animacja algorytmu z wykorzystaniem odległości Warda. Czarne kropki to punkty, szare obszary to większe skupiska, niebieskie strzałki wskazują najbliższych sąsiadów, a czerwony pasek wskazuje bieżący łańcuch. Dla uproszczenia wizualnego, gdy scalanie pozostawia pusty łańcuch, jest kontynuowane z niedawno scalonym klastrem.

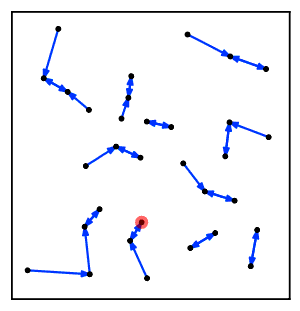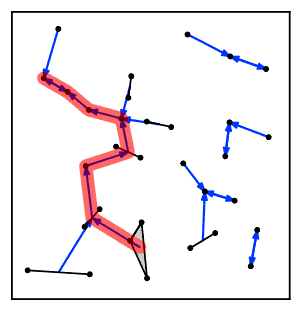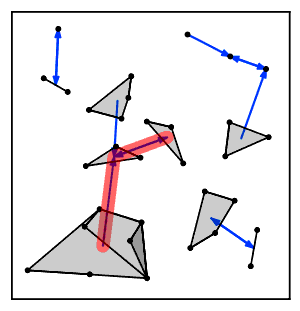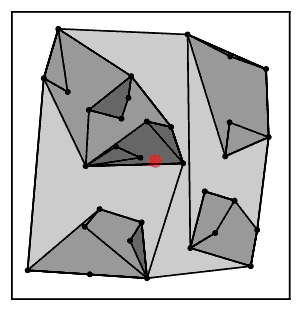
Intuicyjnie, algorytm łańcucha najbliższego sąsiada wielokrotnie podąża za łańcuchem klastrów A → B → C → ... , gdzie każdy klaster jest najbliższym sąsiadem poprzedniego, aż do osiągnięcia pary klastrów, które są najbliższymi sąsiadami.

Bardziej szczegółowo, algorytm wykonuje następujące kroki:

• Zainicjuj zestaw aktywnych klastrów, aby składał się z n klastrów jednopunktowych, po jednym dla każdego punktu wejściowego.
• Niech S będzie strukturą danych stosu , początkowo pustą, której elementami będą aktywne klastry.
• Gdy w zbiorze klastrów jest więcej niż jeden klaster:
  • Jeśli S jest pusty, wybierz dowolnie aktywny klaster i wepchnij go na S .
  • Niech C będzie aktywnym klastrem na górze S . Oblicz odległości od C do wszystkich innych gromad i niech D będzie najbliższą inną gromadą.
  • Jeśli D jest już w S , musi być bezpośrednim poprzednikiem C . Zdejmij oba klastry z S i połącz je.
  • W przeciwnym razie, jeśli D nie jest już w S , wepchnij go na S .

Gdy możliwe jest, aby jeden klaster miał wielu równych najbliższych sąsiadów, algorytm wymaga spójnej reguły rozstrzygania remisów. Na przykład można przypisać dowolne numery indeksów wszystkim klastrom, a następnie wybrać (spośród równych najbliższych sąsiadów) ten, który ma najmniejszy numer indeksu. Ta reguła zapobiega pewnym rodzajom niespójnych zachowań w algorytmie; na przykład bez takiej reguły sąsiedni klaster D mógłby wystąpić na stosie wcześniej niż jako poprzednik C .

Analiza czasu i przestrzeni

Każda iteracja pętli wykonuje pojedyncze wyszukiwanie najbliższego sąsiada klastra i albo dodaje jeden klaster do stosu, albo usuwa z niego dwa klastry. Każdy klaster jest dodawany do stosu tylko raz, ponieważ po ponownym usunięciu jest natychmiast dezaktywowany i scalany. W sumie do stosu dodawane są 2 n - 2 klastrów: n klastrów jednopunktowych w zestawie początkowym i n - 2 wewnętrzne węzły inne niż korzeń w drzewie binarnym reprezentującym grupowanie. Dlatego algorytm wykonuje 2 n − 2 wypychanie iteracji i n - 1 wyskakiwanie iteracji.

Każda z tych iteracji może poświęcić czas na skanowanie aż n - 1 odległości między klastrami w celu znalezienia najbliższego sąsiada. Całkowita liczba obliczeń odległości, które wykonuje, jest zatem mniejsza niż 3 n ² . Z tego samego powodu całkowity czas używany przez algorytm poza tymi obliczeniami odległości wynosi O( n ² ) .

Ponieważ jedyną strukturą danych jest zbiór aktywnych klastrów i stos zawierający podzbiór aktywnych klastrów, wymagana przestrzeń jest liniowa pod względem liczby punktów wejściowych.

Poprawność

Aby algorytm był poprawny, musi być tak, że zdejmowanie i łączenie dwóch górnych klastrów ze stosu algorytmu zachowuje właściwość, że pozostałe klastry na stosie tworzą łańcuch najbliższych sąsiadów. Dodatkowo powinno być tak, że wszystkie klastry utworzone podczas algorytmu są takie same, jak klastry utworzone przez algorytm zachłanny , który zawsze łączy dwa najbliższe skupienia, mimo że algorytm zachłanny generalnie będzie przeprowadzał scalanie w innej kolejności niż algorytm łańcucha najbliższego sąsiada. Obie te właściwości zależą od konkretnego wyboru sposobu pomiaru odległości między klastrami.

Poprawność tego algorytmu polega na właściwości jego funkcji odległości zwanej redukowalnością . Właściwość ta została zidentyfikowana przez Bruynooghe (1977) w związku z wcześniejszą metodą grupowania, która wykorzystywała pary najbliższych najbliższych sąsiadów, ale nie łańcuchy najbliższych sąsiadów. Funkcja odległości d na klastrach jest zdefiniowana jako redukowalna, jeśli dla każdych trzech klastrów A , B i C w zachłannym hierarchicznym grupowaniu, tak że A i B są najbliższymi sąsiadami, zachodzi następująca nierówność:

re ( ZA ∪ b , do ) ≥ min (re ( ZA , do ), re ( b , do )) .

Jeśli funkcja odległości ma właściwość redukowalności, to połączenie dwóch klastrów C i D może spowodować zmianę najbliższego sąsiada E tylko wtedy, gdy ten najbliższy sąsiad był jednym z C i D . Ma to dwie ważne konsekwencje dla algorytmu łańcucha najbliższego sąsiada. Po pierwsze, można pokazać za pomocą tej właściwości, że na każdym kroku algorytmu klastry na stosie S tworzą prawidłowy łańcuch najbliższych sąsiadów, ponieważ za każdym razem, gdy najbliższy sąsiad zostaje unieważniony, jest natychmiast usuwany ze stosu.

Po drugie, co jeszcze ważniejsze, z tej własności wynika, że ​​jeśli dwa skupienia C i D należą do zachłannego hierarchicznego skupienia i są najbliższymi sąsiadami w dowolnym momencie, to zostaną one połączone przez zachłanne skupienie, na przykład muszą pozostać najbliższymi sąsiadami, dopóki nie zostaną połączone. Wynika z tego, że każda para najbliższych sąsiadów znaleziona przez algorytm łańcucha najbliższego sąsiada jest również parą klastrów znalezionych przez algorytm zachłanny, a zatem algorytm łańcucha najbliższego sąsiada oblicza dokładnie takie samo grupowanie (choć w innej kolejności) jak algorytm zachłanny algorytm.

Zastosowanie do określonych odległości klastrowania

Metoda Warda

Metoda Warda jest aglomeracyjną metodą grupowania, w której odmienność między dwoma skupieniami A i B jest mierzona wielkością, o jaką połączenie dwóch skupień w jedno większe skupienie zwiększyłoby średnią kwadratową odległości punktu od jego środka ciężkości skupienia . To jest,

${\ Displaystyle d (A, B) = \ suma _ {x \ w A, y \ w B} {\ Frac {d ^ {2} (x, y)}} - \sum _{x,y\in A}{\frac {d^{2}(x,y)}{|A|}}-\sum _{x,y\in B}{\frac {d^ {2}(x,y)}{|B|}}.}$

Wyrażona jako środek ciężkości $ZA$ liczności dwóch klastrów, ma prostszy wzór do $A}}$

${\ Displaystyle d (A, B) = {\ Frac {d ^ {2} (c_ {a} ,c_{b})}{1/n_{A}+1/n_{B}}},}$

pozwalając na obliczenie go w stałym czasie na obliczenie odległości. Chociaż metoda Warda jest bardzo wrażliwa na wartości odstające , jest najpopularniejszą odmianą grupowania aglomeracyjnego, zarówno ze względu na okrągły kształt klastrów, które zwykle tworzy, jak i ze względu na swoją pryncypialną definicję jako skupienia, które na każdym etapie ma najmniejszą wariancję w swoich skupieniach. Alternatywnie, tę odległość można postrzegać jako różnicę w koszcie k-średnich między nowym klastrem a dwoma starymi klastrami.

Odległość Warda jest również redukowalna, co można łatwiej zobaczyć na podstawie innego wzoru do obliczania odległości połączonej gromady od odległości klastrów, z których została połączona:

${\ Displaystyle d (A \ kubek B, C) = {\ Frac {n_ {A} + n_ {C}} {n_ {A} + n_ {B} + n_ {C}}} d (A, C) +{\frac {n_{B}+n_{C}}{n_{A}+n_{B}+n_{C}}}d(B,C)-{\frac {n_{C}}{n_ {A}+n_{B}+n_{C}}}d(A,B).}$

Formuły aktualizacji odległości, takie jak ta, nazywane są formułami „typu Lance-Williamsa” po pracy Lance'a i Williamsa (1967) . Jeśli jest najmniejszą z trzech odległości po prawej stronie (co z konieczności byłoby prawdą, gdyby $, b$ były to $)$$Displaystyle d (A,$ wzajemni najbliżsi sąsiedzi), wówczas ujemny wkład z jego okresu jest anulowany przez ${\ displaystyle n_ {C}}$ współczynnik jednego z dwóch pozostałych wyrazów, pozostawiając dodatnią wartość dodaną do średniej ważonej pozostałych dwóch odległości. Dlatego połączona odległość jest $Displaystyle d (B$ co najmniej tak duża, jak minimum i $\$ spotkanie Definicja redukowalności.

Ponieważ odległość Warda jest redukowalna, algorytm łańcucha najbliższego sąsiada wykorzystujący odległość Warda oblicza dokładnie takie samo grupowanie, jak standardowy algorytm zachłanny. Dla n punktów w przestrzeni euklidesowej o stałym wymiarze potrzebny jest czas O ( n ² ) i przestrzeń O ( n ) .

Kompletne połączenie i średnia odległość

Całkowite powiązanie lub grupowanie z najdalszymi sąsiadami to forma grupowania aglomeracyjnego, która definiuje odmienność między klastrami jako maksymalną odległość między dowolnymi dwoma punktami z dwóch klastrów. Podobnie grupowanie na średnich odległościach wykorzystuje średnią odległość parami jako odmienność. Podobnie jak odległość Warda, te dwie formy grupowania są zgodne ze wzorem typu Lance-Williams. powiązaniu odległość jest maksymalną z dwóch odległości $\ Displaystyle d (A \ cup B, C)$${\ Displaystyle d (A, C)}$ i re $\ Displaystyle d (B, C)}$ . Dlatego jest co najmniej równa minimum z tych dwóch odległości, wymogowi redukowalności. W przypadku średniej odległości $}$ d $i$ jest po prostu średnią ważoną ${\ Displaystyle d (B, C)}$ . Ponownie, jest to co najmniej tak duże, jak minimum z dwóch odległości. Zatem w obu przypadkach odległość jest redukowalna.

W przeciwieństwie do metody Warda, te dwie formy grupowania nie mają metody obliczania odległości między parami klastrów w czasie stałym. Zamiast tego możliwe jest zachowanie tablicy odległości między wszystkimi parami klastrów. Ilekroć dwa klastry są łączone, formuła może być użyta do obliczenia odległości między połączonym klastrem a wszystkimi innymi klastrami. Utrzymanie tej tablicy w trakcie działania algorytmu grupowania wymaga czasu i przestrzeni O ( n ² ) . Algorytm łańcucha najbliższego sąsiada może być użyty w połączeniu z tą tablicą odległości, aby znaleźć takie samo grupowanie, jak algorytm zachłanny dla tych przypadków. Jego całkowity czas i przestrzeń, przy użyciu tej tablicy, również wynosi O ( n ² ) .

Te same granice czasowe i przestrzenne ^{kolejki priorytetów opartą na drzewie} O ( n2 ) można również osiągnąć w inny sposób, za pomocą techniki, która nakłada strukturę danych czwórkowym na wierzch macierzy odległości i wykorzystuje ją do wykonania standardowego algorytmu zachłannego grupowania. Ta metoda quadtree jest bardziej ogólna, ponieważ działa nawet w przypadku metod grupowania, których nie można zredukować. Jednak algorytm łańcucha najbliższego sąsiada dopasowuje swoje ograniczenia czasowe i przestrzenne, używając prostszych struktur danych.

Pojedyncze połączenie

W klastrach z pojedynczym powiązaniem lub z najbliższym sąsiadem, najstarszej postaci aglomeracyjnego hierarchicznego grupowania, odmienność między klastrami jest mierzona jako minimalna odległość między dowolnymi dwoma punktami od dwóch klastrów. Z tą odmiennością,

${\ Displaystyle d (A \ kubek B, C) = \ min (d (A, C), re (PNE)),}$

spełnia jako równość, a nie nierówność, wymóg redukowalności. (Pojedyncze powiązanie jest również zgodne ze wzorem Lance-Williamsa, ale z ujemnym współczynnikiem, na podstawie którego trudniej jest udowodnić redukowalność).

Podobnie jak w przypadku całkowitego powiązania i średniej odległości, trudność obliczenia odległości klastrów powoduje, że algorytm łańcucha najbliższego sąsiedztwa wymaga czasu i przestrzeni O ( n ² ) , aby obliczyć klastrowanie z pojedynczym powiązaniem. Jednak grupowanie z pojedynczym powiązaniem można znaleźć wydajniej za pomocą alternatywnego algorytmu, który oblicza minimalne drzewo rozpinające odległości wejściowych za pomocą algorytmu Prima , a następnie sortuje minimalne krawędzie drzewa rozpinającego i używa tej posortowanej listy do kierowania łączeniem par klastrów. W algorytmie Prim każdą kolejną minimalną krawędź drzewa rozpinającego można znaleźć poprzez sekwencyjne przeszukiwanie nieposortowanej listy najmniejszych krawędzi łączących częściowo skonstruowane drzewo z każdym dodatkowym wierzchołkiem. Ten wybór oszczędza czas, który algorytm poświęciłby na dostosowywanie wag wierzchołków w swojej kolejce priorytetów . Użycie algorytmu Prima w ten sposób zajęłoby czas O ( n ² ) i przestrzeń O ( n ) , dopasowując najlepsze granice, jakie można osiągnąć za pomocą algorytmu łańcucha najbliższego sąsiada dla odległości z obliczeniami w czasie stałym.

Odległość środka ciężkości

Inną miarą odległości powszechnie stosowaną w klastrowaniu aglomeracyjnym jest odległość między środkami ciężkości par klastrów, znana również jako metoda grup ważonych. Można to łatwo obliczyć w stałym czasie na obliczenie odległości. Nie jest to jednak redukowalne. Na przykład, jeśli dane wejściowe tworzą zestaw trzech punktów trójkąta równobocznego, połączenie dwóch z tych punktów w większy klaster powoduje zmniejszenie odległości między klastrami, co jest naruszeniem redukowalności. Dlatego algorytm łańcucha najbliższego sąsiada niekoniecznie znajdzie to samo skupienie, co algorytm zachłanny. Niemniej Murtagh (1983) pisze, że algorytm łańcucha najbliższego sąsiada zapewnia „dobrą heurystykę” dla metody środka ciężkości. Inny algorytm autorstwa Daya i Edelsbrunnera (1984) może być użyty do znalezienia zachłannego skupienia w czasie O ( n ² ) dla tej miary odległości.

Odległości wrażliwe na kolejność scalania

Powyższa prezentacja wyraźnie zabroniła odległości wrażliwych na kolejność scalania. Rzeczywiście, dopuszczanie takich odległości może powodować problemy. W szczególności istnieją odległości klastra wrażliwe na kolejność, które spełniają redukowalność, ale dla których powyższy algorytm zwróci hierarchię z kosztami suboptymalnymi. Dlatego, gdy odległości klastrów są definiowane za pomocą formuły rekurencyjnej (jak niektóre z omówionych powyżej), należy uważać, aby nie używały one hierarchii w sposób wrażliwy na kolejność scalania.

Historia

Algorytm łańcucha najbliższego sąsiada został opracowany i wdrożony w 1982 roku przez Jean-Paula Benzécriego i J. Juana. Oparli ten algorytm na wcześniejszych metodach, które konstruowały hierarchiczne skupienia przy użyciu par najbliższych najbliższych sąsiadów bez wykorzystywania łańcuchów najbliższych sąsiadów.