Skan Grahama

Demo skanowania Grahama w celu znalezienia wypukłego kadłuba 2D.

Skan Grahama jest metodą znajdowania otoczki wypukłej skończonego zbioru punktów na płaszczyźnie o złożoności czasowej O ( n log n ). Został nazwany na cześć Ronalda Grahama , który opublikował oryginalny algorytm w 1972 roku. Algorytm znajduje wszystkie wierzchołki otoczki wypukłej uporządkowane wzdłuż jej granicy. Używa stosu do skutecznego wykrywania i usuwania wklęsłości na granicy.

Algorytm

Jak widać, PAB i ABC są przeciwne do ruchu wskazówek zegara, ale BCD nie. Algorytm wykrywa tę sytuację i odrzuca wcześniej wybrane segmenty, dopóki nie zostanie wykonany obrót w kierunku przeciwnym do ruchu wskazówek zegara (w tym przypadku ABD).

Pierwszym krokiem w tym algorytmie jest znalezienie punktu o najniższej współrzędnej y. Jeżeli najniższa współrzędna y występuje w więcej niż jednym punkcie zbioru, należy wybrać punkt o najniższej współrzędnej x spośród kandydatów. ten punkt P. Ten krok trwa O ( n ), gdzie n jest liczbą rozpatrywanych punktów.

Następnie zbiór punktów należy posortować rosnąco według kąta, jaki tworzą one i punkt P z osią x. Do tego odpowiedni jest dowolny algorytm sortowania ogólnego przeznaczenia , na przykład sortowanie na stosie (czyli O( n log n )).

Sortowanie według kąta nie wymaga obliczania kąta. Możliwe jest użycie dowolnej funkcji kąta, która jest monotoniczna w przedziale. ${\ Displaystyle [0, \ pi]}$ . Cosinus można łatwo obliczyć za pomocą iloczynu skalarnego lub można użyć nachylenia linii. Jeśli w grę wchodzi precyzja numeryczna, funkcja porównania używana przez algorytm sortowania może użyć znaku krzyżowego do określenia względnych kątów.

, albo zerwij powiązania, zwiększając odległość ( w celu ułatwienia obliczeń można użyć odległości Manhattanu lub Czebyszewa , ponieważ punkty leżą na tym samym promieniu), albo usuń wszystkie oprócz najdalszego punktu.

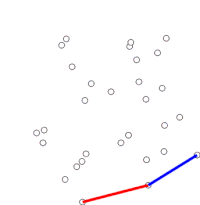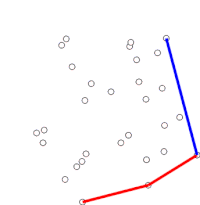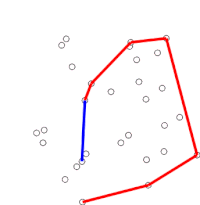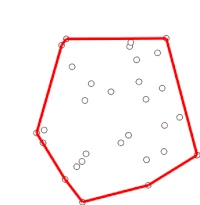
Algorytm kontynuuje, rozważając kolejno każdy punkt w posortowanej tablicy. Dla każdego punktu określa się najpierw, czy przejazd z dwóch punktów bezpośrednio poprzedzających ten punkt stanowi skręt w lewo, czy w prawo. W przypadku skrętu w prawo przedostatni punkt nie jest częścią wypukłej otoczki i leży „wewnątrz” niej. To samo określenie jest następnie wykonywane dla zestawu ostatniego punktu i dwóch punktów, które bezpośrednio poprzedzają punkt, w którym stwierdzono, że znajdował się wewnątrz kadłuba, i jest powtarzane do momentu napotkania zestawu „skrętu w lewo”, w którym to momencie algorytm przechodzi dalej do następnego punktu w zbiorze punktów w posortowanej tablicy pomniejszonej o wszelkie znalezione punkty znajdujące się wewnątrz kadłuba; nie ma potrzeby ponownego rozważania tych punktów. (Jeśli na dowolnym etapie trzy punkty są współliniowe, można zdecydować się na odrzucenie lub zgłoszenie, ponieważ w niektórych zastosowaniach wymagane jest znalezienie wszystkich punktów na granicy otoczki wypukłej.)

Ponownie, określenie, czy trzy punkty stanowią „skręt w lewo”, czy „skręt w prawo”, nie wymaga obliczania rzeczywistego kąta między dwoma odcinkami linii i można to faktycznie osiągnąć jedynie za pomocą prostej arytmetyki. dla trzech punktów ${\ Displaystyle P_ {1} = (x_ {1}, y_ {1})}$ , ${\ Displaystyle P_ {2 }=(x_{2},y_{2})}$ i ${\ Displaystyle P_ {3} = (x_ {3}, y_ {3})}$ , oblicz współrzędną z iloczynu krzyżowego dwóch wektorów ${\ Displaystyle { \ overrightarrow {P_ {1} P_ {2}}}}$ i ${\ Displaystyle {\ overrightarrow {P_ {1} P_ {3}}}}$ , co jest określone wyrażeniem ${\ Displaystyle (x_ {2} -x_ {1}) (y_ {3} -y_ {1}) - (y_ { 2}-y_{1})(x_{3}-x_{1})}$ . Jeśli wynikiem jest 0, punkty są współliniowe; jeśli jest dodatni, trzy punkty stanowią „skręt w lewo” lub orientację przeciwną do ruchu wskazówek zegara, w przeciwnym razie „skręt w prawo” lub orientację zgodnie z ruchem wskazówek zegara (dla punktów numerowanych przeciwnie do ruchu wskazówek zegara).

Ten proces ostatecznie powróci do punktu, w którym się rozpoczął, w którym to momencie algorytm jest zakończony, a stos zawiera teraz punkty na wypukłym kadłubie w kolejności przeciwnej do ruchu wskazówek zegara.

Złożoność czasowa

Sortowanie punktów ma złożoność czasową O( n log n ). Choć może się wydawać, że złożoność czasowa pętli wynosi O( n ² ), ponieważ dla każdego punktu cofa się, aby sprawdzić, czy któryś z poprzednich punktów wykonuje „skręt w prawo”, tak naprawdę jest to O( n ), ponieważ każdy punkt jest rozpatrywany co najwyżej dwa razy w pewnym sensie. Każdy $punkt może$ tylko raz jako punkt w „skręcie w lewo” (ponieważ ${\ Displaystyle (x_ {3}, y_ {3})}$ po tym) i jako punkt ${\ Displaystyle (x_ {2}, y_ {2} )} w „$$w$ punkt jest Całkowita złożoność czasowa wynosi zatem O( n log n ), ponieważ czas sortowania dominuje nad czasem faktycznego obliczenia wypukłej otoczki.

Pseudo kod

Poniższy pseudokod wykorzystuje funkcję ccw: ccw > 0, jeśli trzy punkty wykonują obrót w kierunku przeciwnym do ruchu wskazówek zegara, zgodnie z ruchem wskazówek zegara, jeśli ccw < 0, i współliniowo, jeśli ccw = 0. (W rzeczywistych aplikacjach, jeśli współrzędne są dowolnymi liczbami rzeczywistymi, funkcja wymaga dokładne porównanie liczb zmiennoprzecinkowych i należy wystrzegać się liczbowych osobliwości dla „prawie” punktów współliniowych).

Następnie pozwól, aby wynik był przechowywany w stosie .

  niech  points  będą  listą punktów  niech  stack = empty_stack()  znajdzie  najniższą współrzędną y i najbardziej wysunięty na lewo punkt, zwany P0  sortuj  punkty według kąta biegunowego z P0, jeśli kilka punktów ma ten sam kąt biegunowy to zachowaj tylko  najdalszy  punkt  w  punktach : # wyjmij ostatni punkt ze stosu, jeśli obrócimy się zgodnie z ruchem wskazówek zegara, aby osiągnąć ten punkt,  podczas gdy  count  stack > 1 i  ccw  (next_to_top(stack), top(stack), point) <= 0:  pop  stack  punkt  pchnięcia  do  końca  stosu 

Teraz stos zawiera wypukły kadłub, w którym punkty są zorientowane przeciwnie do ruchu wskazówek zegara, a P0 jest pierwszym punktem.

Tutaj next_to_top() jest funkcją zwracającą element jeden wpis poniżej wierzchołka stosu, bez zmiany stosu, i podobnie top() zwraca element znajdujący się najwyżej.

Ten pseudokod jest adaptacją Wstępu do algorytmów .

Notatki

Ta sama podstawowa idea działa również wtedy, gdy dane wejściowe są sortowane według współrzędnej x zamiast kąta, a kadłub jest obliczany w dwóch krokach, tworząc odpowiednio górną i dolną część kadłuba. Ta modyfikacja została opracowana przez AM Andrew. Ma te same podstawowe właściwości co skan Grahama.

Oryginalny opis Grahama obejmował sortowanie wokół wewnętrznego punktu wypukłej otoczki , a nie jednego z jej wierzchołków. W przypadku tego samego wyboru punktu obrotu dla algorytmu sortowania, połączenie wszystkich innych punktów w ich posortowanej kolejności wokół tego punktu, zamiast wykonywania pozostałych kroków skanowania Grahama, tworzy wielokąt w kształcie gwiazdy, będący poligonalizacją danych wejściowych .

Technika stosu zastosowana w skanie Grahama jest bardzo podobna do tej w przypadku problemu wszystkich najbliższych mniejszych wartości , a algorytmy równoległe dla wszystkich najbliższych mniejszych wartości mogą być również użyte (takie jak skan Grahama) do wydajnego obliczania wypukłych kadłubów posortowanych sekwencji punktów.

Solidność numeryczna

Odporność numeryczna jest problemem, z którym należy sobie poradzić w algorytmach wykorzystujących arytmetykę komputerową zmiennoprzecinkową o skończonej precyzji . W artykule z 2004 roku przeanalizowano prostą strategię przyrostową, którą można wykorzystać w szczególności do implementacji skanowania Grahama. Zadeklarowanym celem artykułu nie była szczegółowa analiza algorytmu, ale raczej dostarczenie podręcznikowego przykładu tego, co i jak może zawieść z powodu obliczeń zmiennoprzecinkowych w geometrii obliczeniowej . Później D. Jiang i NF Stewart rozwinęli ten temat i wykorzystali analizę błędów wstecznych doszedł do dwóch głównych wniosków. Po pierwsze, otoczka wypukła jest dobrze uwarunkowanym problemem i dlatego można oczekiwać algorytmów, które dają odpowiedź w rozsądnym marginesie błędu. Po drugie, pokazują, że modyfikacja skanu Grahama, którą nazywają Graham-Fortune (zawierająca idee Stevena Fortune'a dotyczące stabilności liczbowej) rzeczywiście przezwycięża problemy skończonej precyzji i niedokładnych danych „w jakim stopniu jest to możliwe”.

Zobacz też

• Algorytmy kadłuba wypukłego

Dalsza lektura

•   Cormen, Thomas H .; Leiserson, Charles E .; Rivest, Ronald L .; Stein, Clifford (2001) [1990]. „33.3: Znalezienie wypukłej otoczki”. Wprowadzenie do algorytmów (wyd. 2). MIT Press i McGraw-Hill. s. 949–955. ISBN 0-262-03293-7 .