Algorytm ośmiopunktowy

Algorytm ośmiopunktowy to algorytm używany w wizji komputerowej do oszacowania podstawowej macierzy lub podstawowej macierzy związanej z parą kamer stereo na podstawie zestawu odpowiednich punktów obrazu. Został wprowadzony przez Christophera Longueta-Higginsa w 1981 roku dla przypadku macierzy esencjalnej. Teoretycznie algorytm ten może być zastosowany również dla macierzy fundamentalnej, ale w praktyce bardziej odpowiedni jest w tym przypadku znormalizowany algorytm ośmiopunktowy , opisany przez Richarda Hartleya w 1997 roku.

Nazwa algorytmu wywodzi się z faktu, że estymuje on podstawową macierz lub podstawową macierz ze zbioru ośmiu (lub więcej) odpowiednich punktów obrazu. Jednak odmiany algorytmu mogą być stosowane dla mniej niż ośmiu punktów.

Ograniczenie współpłaszczyznowości

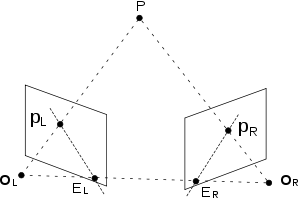
Przykład geometrii epipolarnej. Dwie kamery z odpowiednimi środkami punktów rzutowania O _L i O _R obserwują punkt P . Rzut P na każdą z płaszczyzn obrazu jest oznaczony jako p _L i p _R . Punkty E _L i E _R są epipolami.

Geometrię epipolarną dwóch kamer i punktu w przestrzeni można wyrazić za pomocą równania algebraicznego. $}}$ $\$ bez względu na to, gdzie znajduje się punkt $P$ P { $displaystyle$ $i$ należą tej samej Wywołaj współrzędne punktu w układzie odniesienia lewego oka i wywołaj współrzędne $L {\ displaystyle$ $displaystyle X_ {$ $}}$ w X $L}$ ramka odniesienia prawego oka i wywołanie $=$ i translacji między dwoma ramkami odniesienia st $-T)}$ $X_ {L$ to związek między współrzędnymi $.$ dwóch układach odniesienia Poniższe równanie zawsze obowiązuje, ponieważ wektor wygenerowany z jest ortogonalny zarówno do $T \ klina X_ {L}}:$ $Displaystyle$ $X_ {L}$ klin }

{\ Displaystyle X_ {L} ^ {T} T \ klin X_ {L} -T ^ {T }T\klin X_{L}=(X_{L}-T)^{T}T\klin X_{L}=0}

Ponieważ ${\ Displaystyle I = R ^ {T} R}$ , otrzymujemy

{\ Displaystyle (X_ {L} -T) ^ {T} R ^ {T} RT \ klin X_ {L} = 0}

.

Zastępując ${\ Displaystyle (X_ {L} -T) ^ {T} R ^ {T}}$ przez ${\ Displaystyle X_ {R} ^ {T}}$ , otrzymujemy

{\ Displaystyle X_ {R} ^ {T} RT \ klin X_ {L} = X_ {R} ^ {T }RSX_{L}=X_{R}^{T}EX_{L}=0}

Zauważ, że można traktować jako macierz; ${\ displaystyle T \ klin}$ Longuet-Higgins użył symbolu, $zaznaczyć$ . Produkt jest często nazywany podstawową macierzą i oznaczany przez $\ Displaystyle RT \$ $klin = RS}$ .

${\ Displaystyle {\ overline {O_ {L} p_ {L}}}, {\ overline {O_ {R} p_ {R}}$ } } wektory $i$ współpłaszczyznowości Jeśli nazwiemy współrzędnymi rzutów na lewą i prawą płaszczyznę obrazu, wówczas ograniczenie współpłaszczyznowości można zapisać $jako$ $}$

{\ Displaystyle y' ^ {T} \ mathbf {E} y = 0}

Podstawowy algorytm

Podstawowy algorytm ośmiopunktowy jest tutaj opisany dla przypadku szacowania $podstawowej$ . Składa się z trzech kroków. Najpierw formułuje jednorodne równanie liniowe , którego rozwiązanie jest bezpośrednio związane z , a następnie rozwiązuje równanie, biorąc pod uwagę, że może nie mieć dokładnego $rozwiązania$ Na koniec zarządza się wewnętrznymi ograniczeniami wynikowej macierzy. Pierwszy krok został opisany w artykule Longueta-Higginsa, drugi i trzeci krok to standardowe podejścia w teorii estymacji.

Ograniczenie zdefiniowane przez podstawową macierz jest ${\ displaystyle \ mathbf {E}}$

{\ Displaystyle (\ mathbf {y} ') ^ {T} \, \ mathbf {E} \, \ mathbf {y} = 0}

dla odpowiednich punktów obrazu reprezentowanych w znormalizowanych współrzędnych obrazu ${\ Displaystyle \ mathbf {y} \ mathbf {y} '}$ . Problem, który rozwiązuje algorytm, polega na określeniu $zestawu$ punktów obrazu. $.$ , które dokładnie spełnia powyższe ograniczenie, może nie być możliwe wszystkie punkty. Kwestia ta została omówiona w drugim etapie algorytmu.

Krok 1: Formułowanie jednorodnego równania liniowego

Z

{\ Displaystyle \ mathbf {y} = {\ rozpocząć {pmatrix} y_ {1} \\ y_ {2} \\ 1 \ koniec {pmatrix}}}

i

_

_

{\ Displaystyle \ mathbf {E} = {\ rozpocząć {pmatrix} e_ {11} i e_ {12} i e_ {13} \\ e_ {21}&e_{22}&e_{23}\\e_{31}&e_{32}&e_{33}\end{pmatrix}}}

ograniczenie można również przepisać jako

{\ Displaystyle y'_ {1} y_ {1} e_ {11} + y'_ {1} y_ {2} e_ {12} + y'_ {1} e_ {13} +y'_{2}y_{1}e_{21}+y'_{2}y_{2}e_{22}+y'_{2}e_{23}+y_{1}e_{31} +y_{2}e_{32}+e_{33}=0\,}

Lub

{\ Displaystyle \ mathbf {e} \ cdot {\ tylda {\ mathbf {y}}} = 0}

Gdzie

{\ Displaystyle {\ tylda {\ mathbf {y}}} ={\begin{pmatrix}y'_{1}y_{1}\\y'_{1}y_{2}\\y'_{1}\\y'_{2}y_{1}\ \y'_{2}y_{2}\\y'_{2}\\y_{1}\\y_{2}\\1\end{pmacierz}}}

i

{\ Displaystyle \ mathbf {e} = {\ rozpocząć {pmatrix} e_ {11} \\ e_ {12} \\ e_ {13} \\ e_ {21 }\\e_{22}\\e_{23}\\e_{31}\\e_{32}\\e_{33}\end{pmatrix}}}

to znaczy ${\ Displaystyle \ mathbf {e}}$ reprezentuje podstawową macierz w postaci 9-wymiarowego wektora i ten wektor musi być prostopadły do wektora ${\ Displaystyle {\ tylda {\ mathbf {y}} }}$ $}}$ które można postrzegać jako reprezentację wektorową macierzy $y$ { y} ^ { .

Każda para odpowiednich punktów obrazu tworzy wektor ${\ displaystyle {\ tylda {\ mathbf {y}}}}$ . Biorąc pod uwagę zbiór punktów 3D, $to$ zbiorowi wektorów $} _ {k}}$ i wszystkie muszą zadowolić

{\ Displaystyle \ mathbf {e} \ cdot {\ tylda {\ mathbf {y}}} _ {k} = 0}

dla wektora ${\ Displaystyle \ mathbf {e}}$ . Biorąc pod uwagę wystarczająco wiele ( $}$ najmniej osiem) liniowo niezależnych wektorów, możliwe wyznaczenie $\ Displaystyle \ mathbf {e}$ prosty sposób. Zbierz wszystkie wektory jako kolumny macierzy i musi być tak, że $_ {k}}$ ${\ Displaystyle {\ tylda {\ mathbf {y} }$

{\ Displaystyle \ mathbf {e} ^ {T} \, \ mathbf {Y} = \ mathbf {0}}

Oznacza to, że $jest$ jednorodnego równania liniowego .

Krok 2: Rozwiązanie równania

Standardowe podejście do rozwiązania tego równania implikuje, że $jest$ $prawym$ osobliwym odpowiadającym wartości osobliwej równej zeru $do skonstruowania użyto$ najmniej ośmiu liniowo niezależnych wektorów, wynika z tego, że ten pojedynczy wektor do skonstruowania ${\ displaystyle \ mathbf {Y}} jest unikalny$ $displaystyle \ mathbf {e}}$ można określić , a następnie ${\$

W przypadku, gdy do skonstruowania użyto więcej niż ośmiu odpowiednich punktów, $jest$ , że nie ma on żadnej wartości osobliwej równej zeru. Przypadek ten występuje w praktyce, gdy na współrzędne obrazu wpływają różnego rodzaju szumy. Powszechnym podejściem do radzenia sobie z tą sytuacją jest opisanie jej jako najmniejszych kwadratów ; znajdź , który minimalizuje. ${\ displaystyle \ mathbf {e}}$

{\ Displaystyle \|\ mathbf {e} ^ {T} \, \ mathbf {Y} \|}

kiedy ${\ Displaystyle \|\ mathbf {e} \|=1}$ . Rozwiązaniem jest wybranie $liczby$ pojedynczej odpowiadającego najmniejszej wartości osobliwej ${\ displaystyle \ mathbf {e}}$ . Ponowne uporządkowanie tej $z$ powrotem do $macierzy$ daje wynik tego kroku, określanego tutaj jako $\ mathbf { E} _{\rm {est}}}$ .

Krok 3: Egzekwowanie wewnętrznego ograniczenia

Inną konsekwencją zajmowania się zaszumionymi współrzędnymi obrazu jest to, że wynikowa macierz może nie spełniać wewnętrznego ograniczenia podstawowej macierzy, to znaczy dwie z jej wartości osobliwych są równe i niezerowe, a druga jest zerowa. W zależności od zastosowania mniejsze lub większe odchylenia od ograniczeń wewnętrznych mogą stanowić problem lub nie. Jeśli krytyczne jest, aby oszacowana macierz spełniała wewnętrzne ograniczenia, można to osiągnąć, znajdując macierz rangi 2, która minimalizuje mi $\ displaystyle \ mathbf {E} '}$

\ Displaystyle \|\ mathbf {E} '- \ mathbf {E} _ {\ rm {est}} \ |}

gdzie $macierzą$ wynikową z kroku 2 i Frobeniusa . Rozwiązanie problemu jest podane przez obliczenie najpierw rozkładu na wartości osobliwe mi $_ {\ rm {est}}}$ :

\ Displaystyle \ mathbf {E} _ {\ rm {est}} = \ mathbf {U} \, \ mathbf {S} \, \ mathbf {V} ^ {T}}

gdzie $}}$ $V$ to macierze ortogonalne, a to macierz diagonalna, która zawiera wartości pojedyncze mi $\ displaystyle \mathbf {E} _{\rm {est}}}$ . W idealnym przypadku jeden z elementów ukośnych $być$ mały w porównaniu z pozostałymi dwoma, które powinny być równe. W każdym razie ustaw

{\ Displaystyle \ mathbf {S} '= {\ rozpocząć {pmatrix} s_ {1} i 0 i 0 \\ 0 i s_ {2} i 0 \\ 0 i 0 i 0 \ koniec {pmatrix}}}

gdzie ${\ Displaystyle s_ {1}, s_ {2}} są$ odpowiednio największą i drugą co do wielkości liczbą pojedynczą w ${\ displaystyle \ mathbf {S}} .$ Wreszcie ${\ Displaystyle \ mathbf {E} '}$ jest podane przez

{\ Displaystyle \ mathbf {E} '= \ mathbf {U} \, \ mathbf {S} '\, \ mathbf {V} ^ {T}}

Macierz $jest wynikowym$ podstawowej macierzy dostarczonej przez algorytm

Algorytm znormalizowany

Podstawowy algorytm ośmiopunktowy można w zasadzie wykorzystać również do oszacowania macierzy fundamentalnej ${\ displaystyle \ mathbf {f}}$ . Ograniczeniem definiującym dla jest . ${\ displaystyle \ mathbf {f}}$

{\ Displaystyle (\ mathbf {y} ') ^ {T} \, \ mathbf {F} \, \ mathbf {y} = 0}

gdzie ${\ Displaystyle \ mathbf {y} \ mathbf {y} '}$ są jednorodnymi reprezentacjami odpowiednich współrzędnych obrazu (niekoniecznie znormalizowanych). Oznacza to, że możliwe jest utworzenie macierzy w podobny sposób jak w przypadku macierzy zasadniczej i rozwiązanie równania ${\ displaystyle \ mathbf {Y}}$

{\ Displaystyle \ mathbf {f} ^ {T} \, \ mathbf {Y} = \ mathbf {0}}

dla ${\ displaystyle \ mathbf {F}$ który jest przekształconą wersją $}$ . Postępując zgodnie $z procedurą$ powyżej, można następnie określić na podstawie zestawu ośmiu pasujących punktów. W praktyce jednak otrzymana macierz fundamentalna może nie być przydatna do określania ograniczeń epipolarnych.

Trudność

Problem polega na tym, że wynikowy $często$ źle uwarunkowany . Teoretycznie $są$ niezerowe. W praktyce jednak niektóre z niezerowych wartości osobliwych mogą stać się małe w stosunku do większych. $.$ odpowiednich punktów , gdzie współrzędne są tylko w przybliżeniu poprawne, może nie istnieć dobrze zdefiniowana wartość pojedyncza, którą można określić jako w przybliżeniu zero W konsekwencji rozwiązanie jednorodnego liniowego układu równań może nie być wystarczająco dokładne, aby było użyteczne.

Przyczyna

Hartley odniósł się do tego problemu oszacowania w swoim artykule z 1997 roku. $ich$ analiza problemu pokazuje, że problem jest spowodowany złym rozkładem jednorodnych współrzędnych obrazu w . Typowa jednorodna reprezentacja współrzędnej obrazu 2D to ${\ Displaystyle (y_ {1}, y_ {2}) \,$ }

{\ Displaystyle \ mathbf {y} = {\ rozpocząć {pmatrix} y_ {1} \\ y_ {2} \\ 1 \ koniec {pmatrix}}}

gdzie oba $się$ w zakresie od 0 do 1000–2000 dla $,$ pierwsze dwie współrzędne zmieniają się w znacznie większym zakresie niż trzecia współrzędna. Ponadto, jeśli punkty obrazu, które są używane do konstrukcji, $leżą$ $\ pm (100,100) \,}$ stosunkowo małym obszarze obrazu, na przykład w ${\ Displaystyle (700,700$ $)$ , ponownie wektor mniej więcej w tym samym kierunku dla wszystkich punktów. W konsekwencji $osobliwą,$ pozostałe będą małe.

Rozwiązanie

Jako rozwiązanie tego problemu Hartley zaproponował, aby układ współrzędnych każdego z dwóch obrazów został niezależnie przekształcony w nowy układ współrzędnych zgodnie z następującą zasadą.

Początek nowego układu współrzędnych powinien być wyśrodkowany (mieć swój początek) w środku ciężkości punktów obrazu. Osiąga się to poprzez tłumaczenie pierwotnego pochodzenia na nowe.
Po translacji współrzędne są równomiernie skalowane, tak aby średnia odległości od początku do punktów była równa ${\ displaystyle {\ sqrt {2}}}$ .

Zasada ta zwykle skutkuje odrębną transformacją współrzędnych dla każdego z dwóch obrazów. W rezultacie nowe jednorodne współrzędne obrazu są podane przez ${\ Displaystyle \ mathbf {\ bar {y}}, \ mathbf {\ bar {y}} '}$

{\ Displaystyle \ mathbf {\ bar {y}} = \ mathbf {T} \, \ mathbf {y}} y Ż ′ = T

{\ bar {y} } '=\mathbf {T} '\,\mathbf {y} '}

gdzie ${\ Displaystyle \ mathbf {T} \ mathbf {T} '}$ to transformacje (translacja i skalowanie) ze starych do nowych znormalizowanych współrzędnych obrazu . Ta normalizacja zależy tylko od punktów obrazu, które są używane w pojedynczym obrazie i zasadniczo różni się od znormalizowanych współrzędnych obrazu wytwarzanych przez znormalizowaną kamerę.

Ograniczenie epipolarne oparte na macierzy fundamentalnej można teraz zapisać jako

{\ Displaystyle 0 = (\ mathbf {\ bar {y}} ') ^{T}\,((\mathbf {T} ')^{T})^{-1}\,\mathbf {F} \,\mathbf {T} ^{-1}\,\mathbf {\ bar {y}} = (\mathbf {\bar {y}} ')^{T}\,\mathbf {\bar {F}} \,\mathbf {\bar {y}}}

gdzie ${\ Displaystyle \ mathbf {\ bar {F}} = ((\ mathbf {T} ') ^ {T}) ^ {- 1} \ ,\mathbf {F} \,\mathbf {T} ^{-1}}$ . $,$ że możliwe jest użycie znormalizowanych jednorodnych współrzędnych obrazu podstawowej $.$ podstawowego ośmiopunktowego algorytmu opisanego powyżej

Celem przekształceń normalizacyjnych jest to, że macierz zbudowana ze znormalizowanych współrzędnych obrazu ma ogólnie lepszy numer warunku niż $bar {Y}}$ $displaystyle \ mathbf {\$ $} }$ ma. Oznacza to, że rozwiązanie jest lepiej zdefiniowane jako rozwiązanie równania jednorodnego $¯$ $\mathbf {\ bar {f}}}$ $\ Displaystyle \ mathbf {\ bar {Y}}$ niż jest względny względem $Y}}$ $mathbf$ . Po określeniu i przekształceniu tego ostatniego w $ten$ ${f}}}$ ¯ { $\$ Displaystyle wg

{\ Displaystyle \ mathbf {F} = (\ mathbf {T} ') ^ {T} \, \ mathbf {\ bar {F}} \, \ mathbf {T}}

Ogólnie rzecz biorąc, to oszacowanie macierzy fundamentalnej jest lepsze niż oszacowanie na podstawie nieznormalizowanych współrzędnych.

Używanie mniej niż ośmiu punktów

$się$ do jednego równania ograniczającego na elemencie . Ponieważ $do$ $swobody,$ wyznaczenia powinno wystarczyć tylko pięć par . David Nister zaproponował wydajne rozwiązanie do estymacji macierzy zasadniczej ze zbioru pięciu sparowanych punktów, znane jako algorytm pięciopunktowy. Hartley i in. glin. później zaproponował zmodyfikowany i bardziej stabilny pięciopunktowy algorytm oparty na algorytmie Nistera.

Zobacz też

Dalsza lektura

Richard I. Hartley (czerwiec 1997). „W obronie ośmiopunktowego algorytmu”. Transakcje IEEE dotyczące rozpoznawania wzorców i inteligencji maszynowej . 19 (6): 580–593. doi : 10.1109/34.601246 .

Richarda Hartleya i Andrew Zissermana (2003). Geometria wielu widoków w wizji komputerowej . Wydawnictwo Uniwersytetu Cambridge. ISBN 978-0-521-54051-3 .

H. Christopher Longuet-Higgins (wrzesień 1981). „Algorytm komputerowy do rekonstrukcji sceny z dwóch projekcji”. Natura . 293 (5828): 133–135. Bibcode : 1981Natur.293..133L . doi : 10.1038/293133a0 . S2CID 4327732 .