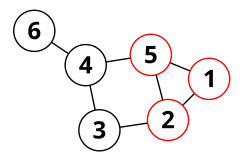
Cykl obwodowy

Na tym wykresie czerwony trójkąt utworzony przez wierzchołki 1, 2 i 5 to cykl peryferyjny: cztery pozostałe krawędzie tworzą pojedynczy most. Jednak pięciokąt 1–2–3–4–5 nie jest peryferyjny, ponieważ dwie pozostałe krawędzie tworzą dwa oddzielne mosty.

W teorii grafów cykl peryferyjny (lub obwód peryferyjny ) w grafie nieskierowanym jest intuicyjnie cyklem , który nie oddziela żadnej części grafu od żadnej innej części. Cykle peryferyjne (lub, jak je początkowo nazywano, peryferyjne wielokąty , ponieważ Tutte nazywał cykle „wielokątami”) zostały po raz pierwszy zbadane przez Tutte (1963) i odgrywają ważną rolę w charakteryzowaniu grafów planarnych i generowaniu przestrzeni cykli grafów niepłaskich.

Definicje

Cykl obwodowy na wykresie można formalnie zdefiniować na jeden z kilku równoważnych sposobów: do $}$ $\ displaystyle$

${\ displaystyle C} jest peryferyjny$ $,$ jeśli jest to prosty cykl na połączonym grafie z właściwością, że dla każdych dwóch krawędzi 2 $displaystyle e_ {2}}$ w $\ Displaystyle G \ setminus C}$ , istnieje ścieżka w ${\ Displaystyle G}$ , która zaczyna się od ${\ Displaystyle e_ {1}}$ , kończy się na ${\ Displaystyle e_ {2}}$ i nie ma wewnętrznych wierzchołków $do$ .
$jest$ $,$ jeśli jest to indukowany z właściwością, że podgraf $jest$ krawędzi i wierzchołków .
Jeśli $displaystyle$ dowolnym podgrafem $,$ mostek jest minimalnym podgrafem sol $\$ $G$ } $displaystyle C}$ który jest rozłączny krawędziowo od do ${\ displaystyle C}$ i który ma tę właściwość, że wszystkie jego punkty mocowania (wierzchołki przylegające do krawędzi zarówno w ${\ Displaystyle B}$ , jak i ${\ Displaystyle G \ setminus B}$ ) należą do do ${\ displaystyle C$ . Prosty cykl $,$ jeśli ma dokładnie jeden mostek.

Równoważność tych definicji nie jest trudna do zauważenia: połączony podwykres $\ Displaystyle G \$ wraz z krawędziami łączącymi go z ) lub akord cyklu, który powoduje sol ∖ do $C$ aby nie zostać wywołanym, musi w każdym przypadku być mostem, a także musi być klasą równoważności relacji binarnej na krawędziach, w których dwie krawędzie są powiązane, jeśli są końcami ścieżki bez wewnętrznych wierzchołków w ${\ styl wyświetlania C}$ .

Nieruchomości

Cykle obwodowe pojawiają się w teorii grafów wielościennych , czyli grafów planarnych połączonych trzema wierzchołkami . Dla każdego płaskiego wykresu $każdego$ płaskiego osadzania powierzchnie osadzania, które są indukowanymi cyklami, muszą być cyklami $peryferyjnymi$ W grafie wielościennym wszystkie ściany są cyklami obwodowymi, a każdy cykl obwodowy jest ścianą. Z tego faktu wynika, że (aż do równoważności kombinatorycznej, wyboru zewnętrznej ściany i orientacji płaszczyzny) każdy graf wielościenny ma unikalne płaskie osadzenie.

W grafach planarnych przestrzeń cykli jest generowana przez ściany, ale w grafach nieplanarnych cykle peryferyjne odgrywają podobną rolę: dla każdego grafu skończonego połączonego z 3 wierzchołkami przestrzeń cykli jest generowana przez cykle peryferyjne. Wynik można również rozszerzyć na lokalnie skończone, ale nieskończone grafy. W szczególności wynika z tego, że grafy 3-połączone z pewnością zawierają cykle peryferyjne. Istnieją grafy 2-połączone, które nie zawierają cykli obwodowych (przykładem jest pełny wykres dwudzielny ${\ Displaystyle K_ {2,4}}$ , dla którego każdy cykl ma dwa mostki), ale jeśli graf spójny z 2 ma co najmniej trzeci stopień, to zawiera co najmniej jeden cykl peryferyjny.

Cykle obwodowe w 3-połączonych grafach mogą być obliczane w czasie liniowym i zostały wykorzystane do projektowania testów planarności. Zostały one również rozszerzone na bardziej ogólne pojęcie nierozdzielnych rozkładów uszu. W niektórych algorytmach testowania planarności grafów przydatne jest znalezienie cyklu, który nie jest peryferyjny, w celu podzielenia problemu na mniejsze podproblemy. W grafie podwójnie połączonym o randze obwodu mniejszej niż trzy (takim jak wykres cyklu lub wykres theta ) każdy cykl jest peryferyjny, ale każdy wykres podwójnie połączony o randze obwodu trzeciej lub wyższej ma cykl nieperyferyjny, który można znaleźć w czasie liniowym.

Uogólniając grafy akordowe , Seymour i Weaver (1984) definiują graf uwiązany jako graf, w którym każdy cykl peryferyjny jest trójkątem. Charakteryzują te grafy jako klikowe sumy grafów akordowych i maksymalnych grafów planarnych .

Pojęcia pokrewne

Cykle peryferyjne były również nazywane cyklami nieseparującymi, ale termin ten jest niejednoznaczny, ponieważ był również używany do dwóch powiązanych, ale odrębnych pojęć: prostych cykli, których usunięcie spowodowałoby rozłączenie pozostałego grafu, oraz cykli topologicznie osadzonego grafu, takiego jak że cięcie wzdłuż cyklu nie spowoduje odłączenia powierzchni, na której osadzony jest wykres.

W matroidach obwód nieseparujący jest obwodem matroidu (to znaczy minimalnym zestawem zależnym) w taki sposób, że usunięcie obwodu pozostawia mniejszą matroidę, która jest połączona (to znaczy, której nie można zapisać jako bezpośrednia suma matroidów) . Są one analogiczne do cykli peryferyjnych, ale nie są takie same nawet w matroidach graficznych (matroidach, których obwody są prostymi cyklami wykresu). Na przykład na pełnym wykresie dwudzielnym ${\ Displaystyle K_ {2,3}}$ , każdy cykl jest peryferyjny (ma tylko jeden mostek, ścieżkę dwukrawędziową), ale matroid graficzny utworzony przez ten mostek nie jest połączony, więc żaden obwód matroidu graficznego K 2 , 3 { $2,3 }}$ nie rozdziela.