Cyklon

W geometrii cyklogon to krzywa wyznaczana przez wierzchołek wielokąta , który toczy się bez poślizgu wzdłuż linii prostej . Nie ma ograniczeń co do charakteru wielokąta. Może to być regularny wielokąt, taki jak trójkąt równoboczny lub kwadrat . Wielokąt nie musi być nawet wypukły : może to być nawet wielokąt w kształcie gwiazdy . Mówiąc bardziej ogólnie, rozważono również krzywe wyznaczane przez punkty inne niż wierzchołki. W takich przypadkach zakłada się, że punkt śledzenia jest sztywno przymocowany do wielokąta. Jeśli punkt śledzenia znajduje się poza wielokątem, wówczas krzywa nazywana jest wydłużonym cyklogonem , a jeśli leży wewnątrz wielokąta, nazywana jest cyklogonem kurtowym .

W granicy, gdy liczba boków wzrasta do nieskończoności, cyklogon staje się cykloidą .

Cyklogon ma ciekawą właściwość dotyczącą swojej powierzchni. Niech $A$ oznacza obszar obszaru powyżej linii i poniżej jednego z łuków, niech $P$ obszar toczącego się wielokąta, a $C$ obszar dysku otaczającego wielokąt. Dla każdego cyklogonu utworzonego przez regularny wielokąt,

{\ Displaystyle A = P + 2C. \,}

Przykłady

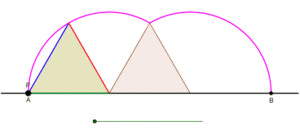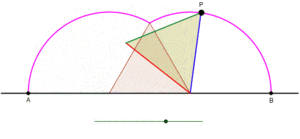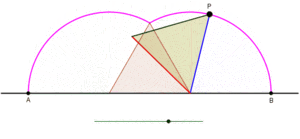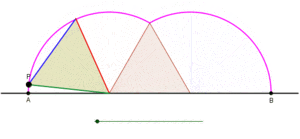
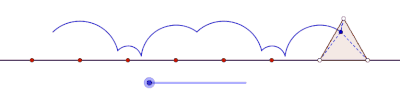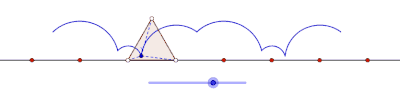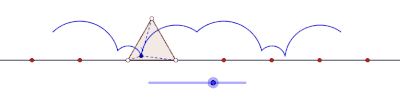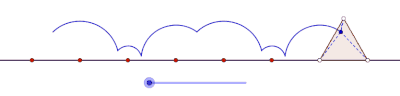
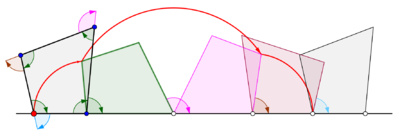
Cyklony generowane przez trójkąt równoboczny i kwadrat

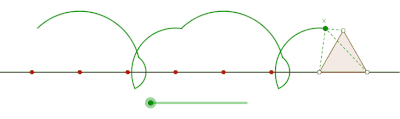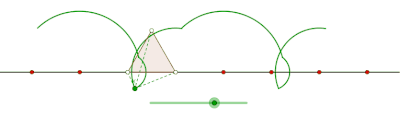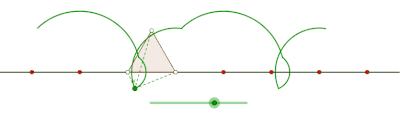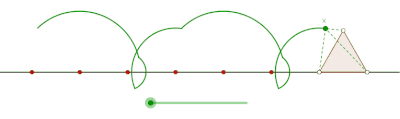
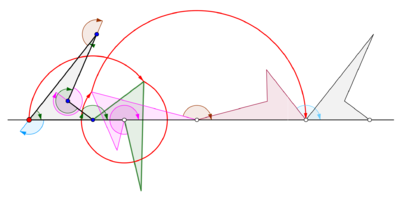
Animacja przedstawiająca generowanie jednego łuku cyklogonu przez trójkąt równoboczny, gdy trójkąt toczy się po linii prostej bez poślizgu.	Animacja przedstawiająca generowanie jednego łuku cyklogonu przez kwadrat, gdy kwadrat toczy się po linii prostej bez poślizgu.

Wydłużony cyklogon generowany przez trójkąt równoboczny

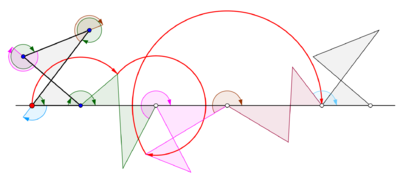
Animacja przedstawiająca śledzenie wydłużonego cyklogonu, gdy trójkąt równoboczny toczy się po linii prostej bez pomijania. Punkt śledzenia X znajduje się poza tarczą trójkąta.

Curtate cyklogon generowany przez trójkąt równoboczny

Animacja przedstawiająca śledzenie cyklogonu kurtowego, gdy trójkąt równoboczny toczy się po linii prostej bez pomijania. Punkt śledzenia Y znajduje się wewnątrz dysku trójkąta.

Cyklony generowane przez czworoboki

Cyklon generowany przez wypukły czworobok

Cyklon generowany przez niewypukły czworobok

Cyklon generowany przez czworobok przypominający gwiazdę

Uogólnione cyklogony

Cyklogon uzyskuje się, gdy wielokąt toczy się po linii prostej. Załóżmy, że wielokąt foremny toczy się po krawędzi innego wielokąta. Załóżmy również, że punkt śledzenia nie jest punktem na granicy wielokąta, ale ewentualnie punktem wewnątrz wielokąta lub na zewnątrz wielokąta, ale leżącym w płaszczyźnie wielokąta. W tej bardziej ogólnej sytuacji niech krzywą wyznacza punkt z na foremnym wielokątnym krążku o n bokach toczącym się wokół innego foremnego wielokątnego krążka o m bokach. Przyjmuje się, że krawędzie dwóch wielokątów foremnych mają tę samą długość. Punkt z przymocowany sztywno do n-kąta wyznacza łuk składający się z n łuków kołowych przed okresowym powtarzaniem wzoru. Ta krzywa nazywa się trochogonem — epitrochogonem , jeśli n-gon toczy się poza m-gonem, a hipotrochogonem , jeśli toczy się wewnątrz m-gonu. Trochogon jest kurkowaty, jeśli z jest wewnątrz n-gonu, i wydłużony (z pętlami), jeśli z jest poza n-gonem. Jeśli z znajduje się w wierzchołku, śledzi epicyklogon lub hipocyklogon.

Zobacz też