Elektroforetyczne rozpraszanie światła

Elektroforetyczne rozpraszanie światła (znane również jako laserowa elektroforeza Dopplera i rozpraszanie światła z wykorzystaniem analizy fazowej ) opiera się na dynamicznym rozpraszaniu światła . Przesunięcie częstotliwości lub przesunięcie fazowe padającej wiązki laserowej zależy od ruchliwości rozproszonych cząstek . W przypadku dynamicznego rozpraszania światła ruchy Browna powodują ruch cząstek. Przy elektroforetycznym rozpraszaniu światła tę funkcję spełnia oscylujące pole elektryczne .

Metodę stosuje się do pomiaru ruchliwości elektroforetycznej , z której następnie można obliczyć potencjał zeta . Instrumenty do stosowania tej metody są dostępne w handlu od kilku producentów. Ostatni zestaw obliczeń wymaga informacji o lepkości i przenikalności dielektrycznej ośrodka dyspersyjnego ; wymagana jest również odpowiednia teoria elektroforezy . Rozcieńczenie próbki jest często konieczne w celu wyeliminowania wielokrotnego rozpraszania padającej wiązki laserowej i/lub interakcji cząstek.

Oprzyrządowanie

Ryc.3. Komercyjny heterodynowy układ optyczny instrumentu do elektroforetycznego rozpraszania światła z modulatorem (z ref. 11).

Wiązka laserowa przechodzi przez komorę elektroforetyczną, naświetla rozproszone w niej cząstki i jest przez nie rozpraszana. Światło rozproszone jest wykrywane przez fotopowielacz po przejściu przez dwa otwory. Istnieją dwa rodzaje układów optycznych: heterodynowe i prążkowe. Ware i Flygare opracowali instrument ELS typu heterodynowego, który był pierwszym instrumentem tego typu. W instrumencie ELS z optyką prążkową wiązka lasera jest dzielona na dwie wiązki. Te krzyżują się wewnątrz komórki do elektroferezy pod stałym kątem, tworząc wzór prążków. Rozproszone światło z cząstek, które migruje wewnątrz prążka, jest modulowane pod względem intensywności. Przesunięcia częstotliwości z obu typów optyki podlegają tym samym równaniom. Obserwowane widma są do siebie podobne. Oka i in. opracowali instrument ELS z optyką typu heterodynowego, który jest obecnie dostępny na rynku. Jego optykę pokazano na ryc. 3.

Jeśli częstotliwości przecinających się wiązek laserowych są takie same, to nie jest możliwe określenie kierunku ruchu migrujących cząstek. Zamiast tego można określić tylko wielkość prędkości (tj. prędkość). Dlatego nie można ustalić znaku potencjału zeta. To ograniczenie można przezwyciężyć, przesuwając częstotliwość jednej z wiązek względem drugiej. Takie przesunięcie można nazwać modulacją częstotliwości lub, bardziej potocznie, po prostu modulacją. Modulatory stosowane w ELS mogą obejmować lustra uruchamiane piezoelektrycznie lub modulatory akustyczno-optyczne. Ten schemat modulacji jest również wykorzystywany w metodzie heterodynowego rozpraszania światła.

Analiza fazowa rozpraszania światła (PALS) to metoda oceny potencjału zeta, w której analizuje się szybkość zmiany fazy interferencji między światłem rozproszonym przez próbkę a modulowaną wiązką odniesienia. Szybkość ta jest porównywana z matematycznie generowaną falą sinusoidalną określoną z góry przez częstotliwość modulatora. Nie jest już wymagane stosowanie dużych pól, które mogą prowadzić do nagrzania próbki i rozpadu koloidów. Jednak jakakolwiek nieliniowość modulatora lub jakakolwiek zmiana charakterystyki modulatora w czasie spowoduje, że generowana fala sinusoidalna nie będzie już odzwierciedlać rzeczywistych warunków, a wynikające z tego pomiary potencjału zeta staną się mniej wiarygodne.

Dalszym rozwinięciem techniki PALS jest tak zwana technika „ciągle monitorowanego PALS” (cmPALS), która dotyczy nieliniowości modulatorów. Dodatkowy modulator wykrywa interferencję między modulowanym i niemodulowanym światłem lasera. Zatem jego częstotliwość uderzeń jest wyłącznie częstotliwością modulacji i dlatego jest niezależna od ruchu elektroforetycznego cząstek. Skutkuje to szybszymi pomiarami, wyższą powtarzalnością nawet przy niewielkich przyłożonych polach elektrycznych oraz wyższą czułością pomiaru.

Heterodynowe rozpraszanie światła

Częstotliwość światła rozproszonego przez cząstki poddawane elektroforezie jest przesunięta o wielkość efektu Dopplera od częstotliwości $\$ światła: $,}$ . Przesunięcie można wykryć za pomocą optyki heterodynowej, w której światło rozpraszające miesza się ze światłem odniesienia. Funkcję autokorelacji natężenia światła mieszanego $7$ opisać następującą tłumioną funkcją cosinus [

{\ Displaystyle g (\ tau) = A + B \ exp (-\Gamma \tau )\cos(2\pi \upsilon _{o})+C\exp(-2\Gamma \tau )\,\qquad (1)}

gdzie jest stałą $rozpadu, a A$ B i C są dodatnimi stałymi zależnymi od układu optycznego.

Częstotliwość tłumienia $.$ częstotliwością i jest różnicą częstotliwości między światłem rozproszonym a referencyjnym

{\ Displaystyle \ upsilon _ {o} = | \ upsilon _ {s} - \ upsilon _ {r} | = | (\ upsilon _ {i} + \ upsilon _ {D}) - (\ upsilon _ {i}+\upsilon _{M})|\qquad (2)}

gdzie ${\ Displaystyle \ upsilon _ {s} \,}$ jest częstotliwością światła rozproszonego, ${\ Displaystyle \ upsilon _ {r} \,}$ częstotliwością światła odniesienia, $\,}$ ${\ Displaystyle \ upsilon _ {i$ $częstotliwość$ częstotliwość padającego światła (światła laserowego) i .

Widmo mocy światła mieszanego, a mianowicie transformata Fouriera $Displaystyle \ pm$ kilka funkcji Lorenza przy $Delta \ upsilon \,$ $połowie$ połowę w

Oprócz tych dwóch, ostatni wyraz w równaniu (1) daje inną funkcję Lorenza w ${\ displaystyle \ upsilon = 0 \,}$

Dopplerowskie przesunięcie częstotliwości i stała zaniku zależą od geometrii układu optycznego i wyrażają się odpowiednio równaniami.

{\ Displaystyle \ upsilon _ {D} = {\ Frac {Vq} {2 \ pi}} \ qquad (3)}

I

{\ Displaystyle \ Gamma = D | q | ^ {2} \ qquad (4)}

gdzie $to$ prędkość cząstek, to $amplituda$ wektora rozpraszania, $to$ dyfuzji cząstek .

Amplituda wektora rozpraszania $określona$ przez równanie

{\ Displaystyle \ | q | = {\ Frac {4 \ pi n} {\ lambda _ {0}}} \ sin \ lewo ({\ Frac {\ theta }{2}}\prawo)\qquad (5)}

Ponieważ prędkość $Displaystyle \ E \$ proporcjonalna do przyłożonego pola elektrycznego, $,}$ pozorna ruchliwość elektroforetyczna ${\ Displaystyle \ \ mu _ {obs} \,}$ jest określony równaniem

{\ Displaystyle \ {\ vec {V}} = \ mu _ {obs} {\ vec {E}} \ qquad (6)}

Wreszcie, zależność między częstotliwością przesunięcia Dopplera a ruchliwością jest podana dla przypadku konfiguracji optycznej z ryc. 3 równaniem

{\ Displaystyle \ upsilon _ {D} = \ mu _ {obs} {\ Frac {nE} {\ lambda _ {0}}} \ sin \ theta \qquad (7)}

gdzie $jest$ natężeniem pola elektrycznego, $współczynnikiem$ załamania światła ośrodka, $\ Displaystyle \ \ lambda _ {0} \$ } długość fali padającego światła w próżni i $.$ rozproszenia Znak jest wynikiem obliczeń $wektorowych i zależy$ optyki.

Częstotliwość widmową można uzyskać zgodnie z równaniem. (2). kiedy ${\ Displaystyle \ |\ upsilon _ {M}|>|\ upsilon _ {D}|\,}$ równ. (2) jest zmodyfikowany i wyrażony jako

{\ Displaystyle \ upsilon _ {p} = \ upsilon _ {o} = \ pm (\ upsilon _ {D} - | \ upsilon _ {M}|)\qquad (8)}

Częstotliwość modulacji $uzyskać$ jako częstotliwość tłumienia bez przyłożonego pola elektrycznego

Średnicę cząstki uzyskuje się zakładając, że cząstka jest kulista. Nazywa się to średnicą hydrodynamiczną ${\ Displaystyle \ d_ {H} \,}$ .

{\ Displaystyle \ d_ {H} = {\ Frac {k_ {B} T} {3 \ pi \ eta D}} \ qquad (10)}

gdzie jest współczynnikiem Boltzmanna , $,$ temperaturą bezwzględną i $}$ dynamiczną otaczającego płynu ${\ displaystyle \ k_ {B}$ \ .

Profil przepływu elektroosmotycznego

Rycina 4 przedstawia dwa przykłady heterodynowych funkcji autokorelacji światła rozproszonego z roztworu siarczanu polistyrenu sodu (NaPSS; MW 400 000; 4 mg/ml w 10 mM NaCl). Oscylacyjna funkcja korelacji pokazana na rys. 4a jest wynikiem interferencji między światłem rozproszonym a zmodulowanym światłem odniesienia. Dudnienie z rys. 4b zawiera dodatkowo udział zmian częstotliwości światła rozproszonego przez cząsteczki PSS w polu elektrycznym 40 V/cm.

Rysunek 5 przedstawia heterodynowe widma mocy uzyskane przez transformatę Fouriera funkcji autokorelacji pokazanych na ryc. 4.

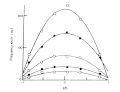
Rycina 6 przedstawia wykresy częstotliwości przesunięcia Dopplera zmierzonych na różnych głębokościach komórek i natężeniach pola elektrycznego, gdzie próbką jest roztwór NaPSS. Te paraboliczne krzywe nazywane są profilami przepływu elektroosmotycznego i wskazują, że prędkość cząstek zmieniała się na różnych głębokościach. Potencjał powierzchniowy ściany komórkowej wytwarza przepływ elektroosmotyczny. Ponieważ komora do elektroforezy jest systemem zamkniętym, w środku komory wytwarzany jest przepływ wsteczny. Następnie obserwowana ruchliwość lub prędkość z równania. (7) jest wynikiem połączenia przepływu osmotycznego i ruchu elektroforetycznego.

Analizę ruchliwości elektroforetycznej przeprowadzili Mori i Okamoto [16], którzy uwzględnili wpływ przepływu elektroosmotycznego na ścianę boczną.

Profil prędkości lub ruchliwości w środku komórki jest określony w przybliżeniu przez równanie. (11) dla przypadku, gdy k>5.

{\ Displaystyle \ U_ {a} (z) = AU_ {0 }(z/b)^{2}+\Delta U_{0}(z/b)+(1-A)U_{0}+U_{p}\qquad (11)}

Gdzie

{\ Displaystyle \ z = \,}

głębokość komórki

{\ Displaystyle \ U_ {a} (z) = \,}

pozorna prędkość elektroforetyczna cząstki w pozycji z.

{\ Displaystyle \ U_ {p} = \,}

prawdziwa prędkość elektroforetyczna cząstek.

{\ Displaystyle \ z/b = \,}

grubość komórki

{\ Displaystyle \ U_ {0} = \,}

średnia prędkość przepływu osmotycznego w górnej i dolnej ścianie komórkowej.

{\ Displaystyle \ Delta U_ {0} = \,}

różnica między prędkościami przepływu osmotycznego w górnej i dolnej ścianie komórkowej.

{\ Displaystyle \ A = {\ Frac {1} {(2/3) - (0,420166 / k)}} \ qquad (12)}

{\ Displaystyle \ k = a/b \,}

stosunek długości dwóch boków prostokątnego przekroju poprzecznego.

Paraboliczna krzywa przesunięcia częstotliwości spowodowanego przepływem elektroosmotycznym pokazana na ryc. 6 pasuje do równania. (11) z zastosowaniem metody najmniejszych kwadratów.

Ponieważ ruchliwość jest proporcjonalna do przesunięcia częstotliwości światła rozpraszanego przez cząstkę i prędkości migracji cząstki, jak wskazuje równanie. (7), wszystkie przesunięcia prędkości, ruchliwości i częstotliwości są wyrażone za pomocą równań parabolicznych. Następnie uzyskano rzeczywistą ruchliwość elektroforetyczną cząstki, ruchliwość elektroosmotyczną na górnej i dolnej ścianie komórkowej. Przesunięcie częstotliwości spowodowane jedynie elektroforezą cząstek jest równe pozornej ruchliwości w warstwie stacjonarnej.

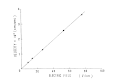
Uzyskana w ten sposób prędkość migracji elektroforetycznej jest proporcjonalna do pola elektrycznego, jak pokazano na ryc. 7. Przesunięcie częstotliwości wzrasta wraz ze wzrostem kąta rozpraszania, jak pokazano na ryc. 8. Wynik ten jest zgodny z teoretycznym równaniem. (7).

Rys. 4 aib; Funkcja korelacji z polem elektrycznym i bez pola elektrycznego. Próbka: roztwór NaPSS (masa cząsteczkowa: 400 000) 4 mg/ml w 10 mM NaCl. Przyłożone pole elektryczne: (a) 0 V/cm; (b) 40 V/cm. Kąt rozpraszania 7,0 stopni, temperatura 25 +-0,3
Rys. 5. Heterodynowe widma mocy otrzymane metodą FFT funkcji korelacji.
Ryc. 6. Przesunięcia częstotliwości obserwowane na różnych głębokościach komórek.
Rys. 7. Zależność prędkości od pola elektrycznego w warstwie stacjonarnej.
Rys. 8. Przesunięcie częstotliwości w funkcji kąta rozpraszania.

Aplikacje

Elektroforetyczne rozpraszanie światła (ELS) jest stosowane przede wszystkim do charakteryzowania ładunków powierzchniowych cząstek koloidalnych, takich jak makrocząsteczki lub syntetyczne polimery (np. polistyren ) w płynnych ośrodkach w polu elektrycznym. Oprócz informacji o ładunkach powierzchniowych ELS może również mierzyć wielkość cząstek białek i określać potencjału zeta .

Biofizyka

ELS jest przydatna do charakteryzowania informacji o powierzchni białek. Ware i Flygare (1971) wykazali, że techniki elektroforetyczne można łączyć ze spektroskopią uderzeniową lasera w celu jednoczesnego określenia ruchliwości elektroforetycznej i współczynnika dyfuzji albuminy surowicy bydlęcej . Szerokość z przesunięciem Dopplera rozproszonego w roztworze makrocząsteczek jest proporcjonalna do współczynnika dyfuzji . Przesunięcie Dopplera jest proporcjonalne do ruchliwości elektroforetycznej makrocząsteczki. Z badań, w których zastosowano tę metodę do poli(L-lizyny) , uważa się, że ELS monitoruje ruchliwość fluktuacji w obecności rozpuszczalników o różnych stężeniach soli. Wykazano również, że dane dotyczące ruchliwości elektroforetycznej można przeliczyć na potencjału zeta , co umożliwia wyznaczenie punktu izoelektrycznego białek oraz liczby ładunków elektrokinetycznych na powierzchni.

Inne makrocząsteczki biologiczne, które można analizować za pomocą ELS, obejmują polisacharydy . Wartości pKa chitozanów można obliczyć z zależności wartości ruchliwości elektroforetycznej od pH i gęstości ładunku. Podobnie jak białka, wielkość i potencjał zeta chitozanów można określić za pomocą ELS.

ELS zastosowano również do kwasów nukleinowych i wirusów. Technikę można rozszerzyć, aby mierzyć ruchliwość elektroforetyczną dużych cząsteczek bakterii przy niskich siłach jonowych.

Nanocząsteczki

ELS został wykorzystany do scharakteryzowania polidyspersyjności , nanodyspersyjności i stabilności jednościennych nanorurek węglowych w środowisku wodnym ze środkami powierzchniowo czynnymi. ^{[ potrzebne źródło ]} Technika ta może być stosowana w połączeniu z dynamicznym rozpraszaniem światła do pomiaru tych właściwości nanorurek w wielu różnych rozpuszczalnikach.

(1) Surfactant Science Series, konsultant ds. konsultacji, konsultant Martin J. Schick, Nowy Jork, tom. 76 Zjawiska elektryczne na interfejsach Wydanie drugie, Podstawy, pomiary i zastosowania, wydanie drugie, poprawione i rozszerzone. Ed: Hiroyuki Ohshima, Kunio Furusawa. 1998. K. Oka i K. Furusawa, rozdział 8 Electrophresis, s. 152 - 223. Marcel Dekker, Inc,

(7) BR Ware i DD Haas, w Fast Method in Physical Biochemistry and Cell Biology. (RI Sha'afi i SM Fernandez, wyd.), Elsevier, Nowy Jork, 1983, rozdz. 8.

(9) Ware, BR; Flygare, WH (1972). „Rozpraszanie światła w mieszaninach BSA, dimerów BSA i fibrynogenu pod wpływem pól elektrycznych”. Journal of Colloid and Interface Science . Elsevier B.V. 39 (3): 670–675. doi : 10.1016/0021-9797(72)90075-6 . ISSN 0021-9797 .

(10) Józefowicz, J.; Hallett, FR (1975-03-01). „Homodyne elektroforetyczne rozpraszanie światła kulek polistyrenowych za pomocą korelacji intensywności wiązki laserowej”. Optyka stosowana . Towarzystwo Optyczne. 14 (3): 740. doi : 10.1364/ao.14.000740 . ISSN 0003-6935 .

(11) K. Oka, W. Otani, K. Kameyama, M. Kidai i T. Takagi, Appl. Teoria. Elektrofor. 1: 273-278 (1990).

(12) K. Oka, W. Otani, Y. Kubo, Y. Zasu i M. Akagi, zgłoszenie patentowe USA. 465, 186: Jpn. Patent H7-5227 (1995).

(16) S. Mori i H. Okamoto, Flotation 28: 1 (1980). (po japońsku): Fusen 28(3): 117 (1980).

(17) M. Smoluchowski, w Handbuch der Electrizitat und des Magnetismus. (L. Greatz. Wyd.). Barth, Lerizig, 1921, s. 379.

(18) P. White, Phil. Mag. S 7, 23, nr 155 (1937).

(19) S. Komagat, rez. Elektrotechnika. Laboratorium. (Jpn) 348, marzec 1933.

(20) Y. Fukui, S. Yuu i K. Ushiki, Power Technol. 54: 165 (1988).