Funkcje testowe do optymalizacji
W matematyce stosowanej funkcje testowe , zwane sztucznymi krajobrazami , są przydatne do oceny właściwości algorytmów optymalizacyjnych, takich jak:
- Współczynnik konwergencji.
- Precyzja.
- Krzepkość.
- Ogólna wydajność.
Tutaj przedstawiono niektóre funkcje testowe, aby dać wyobrażenie o różnych sytuacjach, z jakimi muszą się mierzyć algorytmy optymalizacyjne podczas radzenia sobie z tego rodzaju problemami. W pierwszej części przedstawiono wybrane funkcje celu dla przypadków optymalizacji jednokryterialnej. W drugiej części podano funkcje testowe z odpowiadającymi im frontami Pareto dla wielokryterialnych problemów optymalizacji (MOP).
Przedstawione tutaj sztuczne krajobrazy dla problemów optymalizacji z jednym celem pochodzą z Bäck, Haupt et al. oraz z oprogramowania Rody Oldenhuis. Biorąc pod uwagę liczbę problemów (w sumie 55), tutaj przedstawiono tylko kilka.
Funkcje testowe użyte do oceny algorytmów dla MOP zostały zaczerpnięte z Deb, Binh i in. i Binha. Można pobrać oprogramowanie opracowane przez Deb, które realizuje procedurę NSGA-II z GA, lub program umieszczony w Internecie, który implementuje procedurę NSGA-II z ES.
Podano tylko ogólną postać równania, wykres funkcji celu, granice zmiennych obiektowych oraz współrzędne minimów globalnych.
Funkcje testowe dla optymalizacji jednokryterialnej
| Nazwa | Działka | Formuła | Globalne minimum | Wyszukaj domenę |
|---|---|---|---|---|
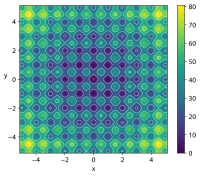
| Funkcja Rastrigina |
|
|
||
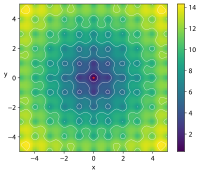
| Funkcja Ackleya |
|
|
||
| Funkcja kuli |

|
, | ||
| Funkcja Rosenbrocka |

|
, | ||
| Funkcja Beale'a |

|
|
||
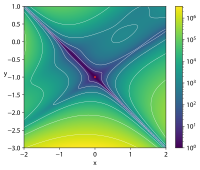
| Funkcja Goldsteina – ceny |
|
|
||
| Funkcja budki |

|
|||
| Funkcja Bukina N.6 |

|
, | ||
| Funkcja Matyasa |

|
|||
| Funkcja Léviego N.13 |

|
|
||
| Funkcja Himmelblaua |
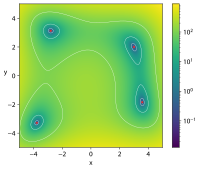
|
|||
| Funkcja wielbłąda z trzema garbami |
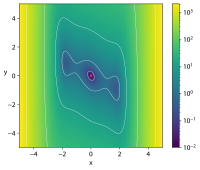
|
|||
| Funkcja Easoma |
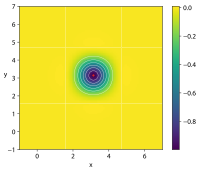
|
|||
| Funkcja cross-in-tray |

|
|||
| Funkcja pojemnika na jajka |
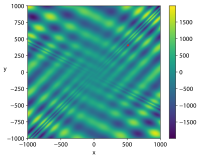
|
|||
| Funkcja stołu Höldera |

|
|||
| Funkcja McCormicka |

|
, | ||
| Funkcja Schaffera nr 2 |
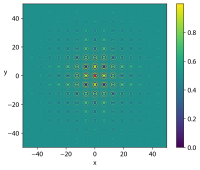
|
|||
| Funkcja Schaffera nr 4 |

|
|||
| Funkcja Styblińskiego-Tanga |
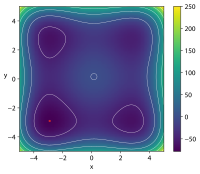
|
, .. |
Funkcje testowe pod kątem optymalizacji z ograniczeniami
Funkcje testowe do optymalizacji wielokryterialnej
[ potrzebne dalsze wyjaśnienia ]
Zobacz też
- Funkcja Ackleya
- Funkcja Himmelblaua
- Funkcja Rastrigina
- Funkcja Rosenbrocka
- Funkcja szekla
- Funkcja Binha
- ^ Powrót, Thomas (1995). Algorytmy ewolucyjne w teorii i praktyce: strategie ewolucyjne, programowanie ewolucyjne, algorytmy genetyczne . Oksford: Oxford University Press. P. 328. ISBN 978-0-19-509971-3 .
- ^ Haupt, Randy L. Haupt, Sue Ellen (2004). Praktyczne algorytmy genetyczne z CD-ROM (wyd. 2). Nowy Jork: J. Wiley. ISBN 978-0-471-45565-3 .
- Bibliografia _ „Wiele funkcji testowych dla globalnych optymalizatorów” . Matematyka . Źródło 1 listopada 2012 r .
- ^ a b c d e Deb, Kalyanmoy (2002) Optymalizacja wielokryterialna przy użyciu algorytmów ewolucyjnych (red. Repr.). Chichester [ua]: Wiley. ISBN 0-471-87339-X .
- ^ ab optymalizacją Binh T. i Korn U. (1997) MOBES: wieloobiektowa strategia ewolucji dla problemów z ograniczoną . W: Materiały z III Międzynarodowej Konferencji Algorytmów Genetycznych. Republika Czeska. s. 176–182
- Wieloobiektywny ^ abc Binh T. (1999) algorytm ewolucyjny. Studium przypadków. Raport techniczny. Instytut Automatyki i Komunikacji. Barleben, Niemcy
- ^ Deb K. (2011) Oprogramowanie dla wielokryterialnego kodu NSGA-II w C. Dostępne pod adresem URL: https://www.iitk.ac.in/kangal/codes.shtml
- ^ Ortiz, Gilberto A. „Optymalizacja wielocelowa przy użyciu ES jako algorytmu ewolucyjnego” . Matematyka . Źródło 1 listopada 2012 r .
- Bibliografia _ Rana, Soraja; Dżubera, Jan; Mathias, Keith E. (1996). „Ocena algorytmów ewolucyjnych”. Sztuczna inteligencja . Elsevier B.V. 85 (1–2): 264. doi : 10.1016/0004-3702(95)00124-7 . ISSN 0004-3702 .
- ^ Vanaret C. (2015) Hybrydyzacja metod przedziałowych i algorytmów ewolucyjnych do rozwiązywania trudnych problemów optymalizacyjnych. praca doktorska. Ecole Nationale de l'Aviation Civile. Institut National Polytechnique de Tuluza, Francja.
- Bibliografia _ Beale, D. (29 września - 2 października 2002). Nowe koncepcje graficznej wizualizacji funkcji celu (PDF) . ASME 2002 Międzynarodowe Konferencje Techniczne Inżynierii Projektowania oraz Konferencja Komputery i Informacje w Inżynierii. Montreal, Kanada. s. 891–897 . Źródło 7 stycznia 2017 r .
- ^ „Rozwiąż problem nieliniowy z ograniczeniami - MATLAB i Simulink” . www.mathworks.com . Źródło 2017-08-29 .
-
^
„Problem z ptakami (ograniczony) | Integracja z Phoenix” . Zarchiwizowane od oryginału w dniu 2016-12-29 . Źródło 2017-08-29 .
{{ cite web }}: CS1 maint: bot: stan oryginalnego adresu URL nieznany ( link ) - ^ Mishra, Sudhanshu (2006). „Niektóre nowe funkcje testowe do globalnej optymalizacji i wydajności metody roju cząstek odpychających” . Papier MPRA .
- ^ Townsend, Alex (styczeń 2014). „Ograniczona optymalizacja w Chebfun” . chebfun.org . Źródło 2017-08-29 .
- ^ Simionescu, Pensylwania (2020). „Zbiór dwuwymiarowych nieliniowych problemów testowych optymalizacji z reprezentacjami graficznymi”. International Journal of Mathematical Modeling and Numerical Optimization . 10 (4): 365–398. doi : 10.1504/IJMMNO.2020.110704 .
- ^ Simionescu, Pensylwania (2014). Wspomagane komputerowo narzędzia do tworzenia wykresów i symulacji dla użytkowników programu AutoCAD (wyd. 1). Boca Raton, Floryda: CRC Press. ISBN 978-1-4822-5290-3 .
- Bibliografia _ Haimes, Jakow Y. (1983). Wieloobiektywne podejmowanie decyzji. Teoria i metodologia . ISBN 0-444-00710-5 .
- Bibliografia _ Fleming, PJ (1995). „Przegląd algorytmów ewolucyjnych w optymalizacji wielokryterialnej”. Komputer Evol . 3 (1): 1–16. CiteSeerX 10.1.1.50.7779 . doi : 10.1162/evco.1995.3.1.1 . S2CID 8530790 .
- ^ F. Kursawe, „ Wariant strategii ewolucji dla optymalizacji wektorów ”, w PPSN I, tom 496 Lect Notes in Comput Sc. Springer-Verlag, 1991, s. 193–197.
- ^ Schaffer, J. David (1984). „Optymalizacja wielu celów za pomocą algorytmów genetycznych ocenianych wektorowo”. W GJE Grefensette; JJ Lawrence Erlbraum (red.). Materiały z Pierwszej Międzynarodowej Konferencji Algorytmów Genetycznych . OCLC 20004572 .
- ^ a b c d e Deb, Kalyan; Thiele L.; Laumanns, Marco; Zitzler, Eckart (2002). „Skalowalne, wielokryterialne problemy testowe optymalizacyjne”. Materiały z Kongresu IEEE 2002 na temat obliczeń ewolucyjnych . Tom. 1. s. 825–830. doi : 10.1109/CEC.2002.1007032 . ISBN 0-7803-7282-4 . S2CID 61001583 .
- ^ Osyczka, A.; Kundu, S. (1 października 1995). „Nowa metoda rozwiązywania uogólnionych problemów optymalizacji wielokryterialnej przy użyciu prostego algorytmu genetycznego”. Optymalizacja strukturalna . 10 (2): 94–99. doi : 10.1007/BF01743536 . ISSN 1615-1488 . S2CID 123433499 .
- Bibliografia _ Gomez-Skarmeta, AF; Sanchez, G.; Deb, K. (maj 2002). „Ewolucyjny algorytm ograniczonej optymalizacji wielokryterialnej”. Materiały z Kongresu 2002 na temat obliczeń ewolucyjnych . CEC'02 (nr kat. 02TH8600) . 2 : 1133–1138. doi : 10.1109/CEC.2002.1004402 . ISBN 0-7803-7282-4 . S2CID 56563996 .
![f(\mathbf {x} )=An+\sum _{i=1}^{n}\left[x_{i}^{2}-A\cos(2\pi x_{i})\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aa1c38ee739ca9cf4582867d74d469df4676cbc)



![{\displaystyle f(x,y)=-20\exp \left[-0.2{\sqrt {0.5\left(x^{2}+y^{2}\right)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f00d1325d65d088f8ae6a96137e62021107921d)
![{\displaystyle -\exp \left[0.5\left(\cos 2\pi x+\cos 2\pi y\right)\right]+e+20}](https://wikimedia.org/api/rest_v1/media/math/render/svg/565ef43958a50fb0ef473bdd46e30bfc725604a7)






![{\displaystyle f({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64863353dcdea2f0ed049cec3aea0a4284d4916a)





![{\displaystyle f(x,y)=\left[1+\left(x+y+1\right)^{2}\left(19-14x+3x^{2}-14y+6xy+3y^{2}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d020ed324ff07759faf17591157771b0e2cdf07)
![{\displaystyle \left[30+\left(2x-3y\right)^{2}\left(18-32x+12x^{2}+48y-36xy+27y^{2}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e562da4f3219f9d66e059441c59e1d299e8557)



















![{\displaystyle f(x,y)=-0.0001\left[\left|\sin x\sin y\exp \left(\left|100-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right|\right)\right|+1\right]^{0.1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d591ae9bcf2feae162cd00398d78bb6870c82946)










![{\displaystyle f(x,y)=0.5+{\frac {\sin ^{2}\left(x^{2}-y^{2}\right)-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/995008c6f10a14b44dac568cc544efb7d5ddd631)
![{\displaystyle f(x,y)=0.5+{\frac {\cos ^{2}\left[\sin \left(\left|x^{2}-y^{2}\right|\right)\right]-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2458c352c0c0524648d8ef713bcea4e80df32fd8)













![{\displaystyle f(x,y)=\sin(y)e^{\left[(1-\cos x)^{2}\right]}+\cos(x)e^{\left[(1-\sin y)^{2}\right]}+(x-y)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7987d4a794d861e7ccd0795265841d3ca172cfae)





![{\displaystyle f(x,y)=-[\cos((x-0.1)y)]^{2}-x\sin(3x+y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dac25f97d0b720512d72c313000d5fb5c7d033a)
![{\displaystyle x^{2}+y^{2}<\left[2\cos t-{\frac {1}{2}}\cos 2t-{\frac {1}{4}}\cos 3t-{\frac {1}{8}}\cos 4t\right]^{2}+[2\sin t]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57168b192e685c6144e3a9527b12087ac7cb11b4)











![{\displaystyle x^{2}+y^{2}\leq \left[r_{T}+r_{S}\cos \left(n\arctan {\frac {x}{y}}\right)\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc42adcc2095ed0c0214a74799db7ee2fac9923)











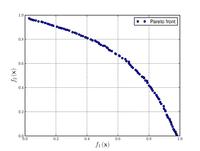
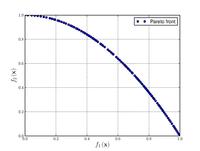
![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}-{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\f_{2}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}+{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3113203c5d455e0e1e6397d57094e80e527b34ba)

![Test function 4.[6]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/3c/Test_function_4_-_Binh.pdf/page1-200px-Test_function_4_-_Binh.pdf.jpg)



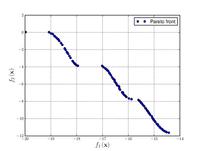
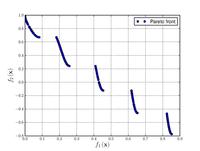
![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{2}\left[-10\exp \left(-0.2{\sqrt {x_{i}^{2}+x_{i+1}^{2}}}\right)\right]\\&\\f_{2}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{3}\left[\left|x_{i}\right|^{0.8}+5\sin \left(x_{i}^{3}\right)\right]\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeb9856144d9869aae4254892ece0fe894dfc152)

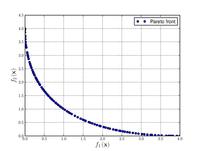








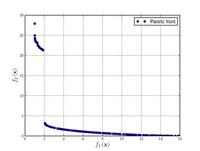
![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=\left[1+\left(A_{1}-B_{1}\left(x,y\right)\right)^{2}+\left(A_{2}-B_{2}\left(x,y\right)\right)^{2}\right]\\f_{2}\left(x,y\right)=\left(x+3\right)^{2}+\left(y+1\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ee5df22af124899c1e268325017ea64e517b51e)








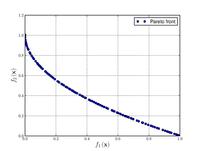




![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left(-4x_{1}\right)\sin ^{6}\left(6\pi x_{1}\right)\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+9\left[{\frac {\sum _{i=2}^{10}x_{i}}{9}}\right]^{0.25}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f03bdd2b0c7a5af33b0a0fc385f9a9c021635d6e)

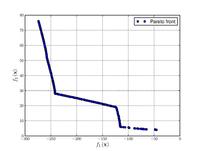





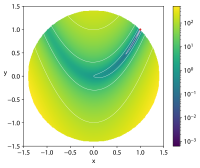
![CTP1 function (2 variables).[4]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/d4/CTP1_function_%282_variables%29.pdf/page1-200px-CTP1_function_%282_variables%29.pdf.jpg)



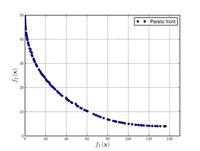
![Constr-Ex problem.[4]](http://upload.wikimedia.org/wikipedia/commons/thumb/6/6f/Constr-Ex_problem.pdf/page1-200px-Constr-Ex_problem.pdf.jpg)