Haszowanie geometryczne

Nie mylić z Geohashingiem .

W informatyce mieszanie geometryczne jest metodą efektywnego znajdowania dwuwymiarowych obiektów reprezentowanych przez dyskretne punkty, które przeszły transformację afiniczną , chociaż istnieją rozszerzenia innych reprezentacji i transformacji obiektów. W kroku offline obiekty są kodowane, traktując każdą parę punktów jako bazę geometryczną . Pozostałe punkty można przedstawić niezmienniczo względem tej bazy za pomocą dwóch parametrów. Dla każdego punktu jego skwantyzowane przekształcone współrzędne są przechowywane w pliku tablica skrótów jako klucz, a indeksy punktów bazowych jako wartość. Następnie wybierana jest nowa para punktów bazowych i proces jest powtarzany. Na etapie on-line (rozpoznania) losowo wybrane pary punktów danych są uznawane za kandydujące bazy. Dla każdej podstawy kandydującej pozostałe punkty danych są kodowane zgodnie z podstawą, a możliwe odpowiedniki obiektu znajdują się w uprzednio skonstruowanej tabeli. Baza kandydująca jest akceptowana, jeśli wystarczająco duża liczba punktów danych indeksuje spójną bazę obiektową.

zostało pierwotnie zasugerowane w wizji komputerowej do rozpoznawania obiektów w 2D i 3D, ale później zostało zastosowane do różnych problemów, takich jak wyrównanie strukturalne białek .

Haszowanie geometryczne w wizji komputerowej

Haszowanie geometryczne to metoda używana do rozpoznawania obiektów. Powiedzmy, że chcemy sprawdzić, czy obraz modelu można zobaczyć na obrazie wejściowym. Można to osiągnąć za pomocą haszowania geometrycznego. Metodę można wykorzystać do rozpoznania jednego z wielu obiektów w bazie, w tym przypadku tablica mieszająca powinna przechowywać nie tylko informacje o ułożeniu, ale także indeks modelu obiektu w bazie.

Przykład

Dla uproszczenia, w tym przykładzie nie użyjemy zbyt wielu obiektów punktowych i założymy, że ich deskryptory są podane tylko przez ich współrzędne (w praktyce deskryptory lokalne , takie jak SIFT , mogą być użyte do indeksowania).

Faza treningu

Punkty obiektu w układzie współrzędnych obrazu oraz osie układu współrzędnych dla podstawy (P2,P4)

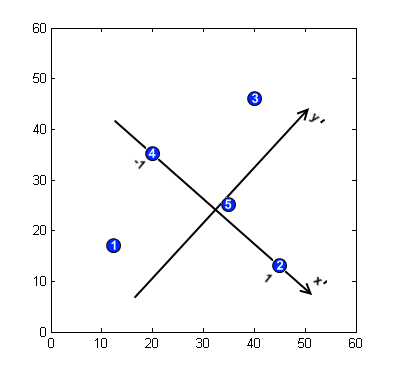
1. Znajdź punkty charakterystyczne modelu. Załóżmy, że na obrazie modelu znajduje się 5 punktów charakterystycznych o współrzędnych ${\ Displaystyle (12,17);}$${\ Displaystyle (45,13);}$${\ Displaystyle (40,46);}$${\ Displaystyle (20,35);}$${\ Displaystyle (35,25)}$ , Zobacz zdjęcie.
2. Wprowadź podstawy do opisu położenia punktów charakterystycznych. Dla przestrzeni 2D i transformacji podobieństwa podstawa jest definiowana przez parę punktów. Punkt początkowy znajduje się na środku odcinka łączącego dwa punkty (w naszym przykładzie P2, P4), oś $y'} }$ skierowana w stronę jednego z nich, oś $displaystyle$ jest prostopadła i przechodzi przez początek. Skala jest dobrana tak, że wartość bezwzględna dla obu punktów bazowych wynosi 1. ${\ displaystyle x'}$
3. Opisz położenie cech względem tej podstawy, czyli oblicz rzuty na nowe osie współrzędnych. Współrzędne powinny być dyskretyzowane, aby rozpoznawanie było odporne na szum, przyjmujemy rozmiar pojemnika 0,25. Otrzymujemy w ten sposób współrzędne ${\ Displaystyle (-0,75, -1,25);}$${\ Displaystyle (1,00,0,00);}$${\ Displaystyle (-0,50,1,25);}$${\ Displaystyle (-1,00,0,00);}$${\ Displaystyle (0,00, 0,25)}$
4. Zapisz podstawę w tablicy skrótów indeksowanej przez cechy (w tym przypadku tylko przekształcone współrzędne). Jeśli obiektów do dopasowania było więcej, powinniśmy również zapisać numer obiektu wraz z parą bazową.
5. Powtórz ten proces dla innej pary bazowej (krok 2). Jest potrzebny do obsługi okluzji . W idealnym przypadku wszystkie niewspółliniowe powinny być wyliczone. Tablicę mieszającą udostępniamy po dwóch iteracjach, do drugiej wybierana jest para (P1, P3).

Tabela skrótów:

wektor ( ${\ Displaystyle x'}$ , ${\ Displaystyle y'}$ )	podstawa
${\ Displaystyle (-0,75, -1,25);}$	(P2,P4)
${\ Displaystyle (1,00, 0,00);}$	(P2,P4)
${\ Displaystyle (-0,50,1,25);}$	(P2,P4)
${\ Displaystyle (-1.00,0.00);}$	(P2,P4)
${\ Displaystyle (0,00, 0,25)}$	(P2,P4)
${\ Displaystyle (1,00, 0,00);}$	(P1,P3)
${\ Displaystyle (0,00, 1,25);}$	(P1,P3)
${\ Displaystyle (-1.00,0.00);}$	(P1,P3)
${\ Displaystyle (0,00, -0,25);}$	(P1,P3)
${\ Displaystyle (0,00,0,50)}$	(P1,P3)

Większość tablic skrótów nie może mieć identycznych kluczy odwzorowanych na różne wartości. Tak więc w prawdziwym życiu nie zakoduje się kluczy bazowych (1.0, 0.0) i (-1.0, 0.0) w tablicy skrótów.

Faza rozpoznania

1. Znajdź interesujące punkty charakterystyczne na obrazie wejściowym.
2. Wybierz dowolną podstawę. Jeśli nie ma odpowiedniej arbitralnej podstawy, prawdopodobnie obraz wejściowy nie zawiera obiektu docelowego.
3. Opisz współrzędne punktów charakterystycznych w nowej bazie. Kwantyzuj otrzymane współrzędne tak, jak to zrobiono wcześniej.
4. Porównaj wszystkie przekształcone cechy punktowe w obrazie wejściowym z tabelą skrótów. Jeśli cechy punktu są identyczne lub podobne, zwiększ liczbę dla odpowiedniej podstawy (i rodzaju obiektu, jeśli istnieje).
5. Dla każdej podstawy, której liczba przekracza określony próg, zweryfikuj hipotezę, że odpowiada ona wybranej w kroku 2 podstawie obrazu. Przenieś układ współrzędnych obrazu do układu modelowego (dla domniemanego obiektu) i spróbuj je dopasować. Jeśli się powiedzie, obiekt zostanie znaleziony. W przeciwnym razie wróć do kroku 2.

Znalezienie lustrzanego wzoru

Wygląda na to, że ta metoda jest w stanie obsłużyć tylko skalowanie, translację i rotację. Jednak obraz wejściowy może zawierać obiekt w transformacji lustrzanej. Dlatego haszowanie geometryczne również powinno być w stanie znaleźć obiekt. Istnieją dwa sposoby wykrywania lustrzanych obiektów.

1. W przypadku wykresu wektorowego uczyń lewą stronę dodatnią, a prawą ujemną. Pomnożenie pozycji x przez -1 da ten sam wynik.
2. Wykorzystaj 3 punkty jako podstawę. Pozwala to na wykrywanie odbić lustrzanych (lub obiektów). W rzeczywistości użycie 3 punktów jako podstawy to inne podejście do mieszania geometrycznego.

Haszowanie geometryczne w wyższych wymiarach

Podobnie jak w powyższym przykładzie, haszowanie dotyczy danych o wyższych wymiarach. W przypadku trójwymiarowych punktów danych potrzebne są również trzy punkty jako podstawa. Pierwsze dwa punkty definiują oś x, a trzeci punkt definiuje oś y (z pierwszym punktem). Oś z jest prostopadła do utworzonej osi przy użyciu reguły prawej ręki. Zauważ, że kolejność punktów wpływa na wynikową podstawę

Zobacz też

• Mieszanie percepcyjne

• Wolfson, HJ i Rigoutsos, I (1997). Haszowanie geometryczne: przegląd. IEEE Nauka i inżynieria obliczeniowa, 4(4), 10-21.