Ilustracja centralnego twierdzenia granicznego

W teorii prawdopodobieństwa centralne twierdzenie graniczne (CLT) stwierdza, że w wielu sytuacjach, gdy dodawane są niezależne zmienne losowe, ich odpowiednio znormalizowana suma dąży do rozkładu normalnego. Ten artykuł zawiera dwie ilustracje tego twierdzenia. Oba obejmują sumę niezależnych i identycznie rozłożonych zmiennych losowych i pokazują, w jaki sposób rozkład prawdopodobieństwa sumy zbliża się do rozkładu normalnego wraz ze wzrostem liczby wyrazów w sumie.

Pierwsza ilustracja dotyczy ciągłego rozkładu prawdopodobieństwa , dla którego zmienne losowe mają funkcję gęstości prawdopodobieństwa . Druga ilustracja, dla której większość obliczeń można wykonać ręcznie, dotyczy dyskretnego rozkładu prawdopodobieństwa , który charakteryzuje się funkcją masy prawdopodobieństwa .

Ilustracja przypadku ciągłego

Gęstość sumy dwóch niezależnych zmiennych losowych o wartościach rzeczywistych jest równa splotowi funkcji gęstości zmiennych pierwotnych.

Zatem gęstość sumy m + n wyrazów ciągu zmiennych niezależnych o identycznym rozkładzie jest równa splotowi gęstości sum m wyrazów i n wyrazu. W szczególności gęstość sumy n + 1 wyrazów jest równa splotowi gęstości sumy n wyrazów z pierwotną gęstością („suma” 1 wyrazu).

Funkcja gęstości prawdopodobieństwa jest pokazana na pierwszym rysunku poniżej. Następnie gęstości sum dwóch, trzech i czterech niezależnych zmiennych o identycznym rozkładzie , z których każda ma pierwotną gęstość, są pokazane na poniższych rysunkach. Jeśli pierwotna gęstość jest wielomianem odcinkowym , jak to jest w przykładzie, to tak samo jest z gęstościami sumarycznymi o coraz wyższym stopniu. Chociaż pierwotna gęstość jest daleka od normalnej, gęstość sumy zaledwie kilku zmiennych o tej gęstości jest znacznie gładsza i ma niektóre cechy jakościowe normalnej gęstości .

₀ Sploty obliczono za pomocą dyskretnej transformaty Fouriera . Skonstruowano listę wartości y = f ( x + k Δ x ), gdzie f jest pierwotną funkcją gęstości, a Δ x jest w przybliżeniu równe 0,002, a k jest równe 0 do 1000. Dyskretna transformata Fouriera Y z y został obliczony. Wtedy splot f z samym sobą jest proporcjonalny do odwrotnej dyskretnej transformaty Fouriera punktowy iloczyn Y z samym sobą .

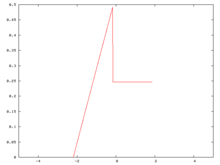
Funkcja gęstości prawdopodobieństwa .

Oryginalna funkcja gęstości prawdopodobieństwa

Zaczynamy od funkcji gęstości prawdopodobieństwa. Ta funkcja, choć nieciągła, jest daleka od najbardziej patologicznego przykładu, jaki można stworzyć. Jest to wielomian częściowy, składający się z fragmentów o stopniach 0 i 1. Średnia tego rozkładu wynosi 0, a jego odchylenie standardowe wynosi 1.

Gęstość sumy dwóch zmiennych .

Funkcja gęstości prawdopodobieństwa sumy dwóch wyrazów

Następnie obliczamy gęstość sumy dwóch zmiennych niezależnych, z których każda ma powyższą gęstość. Gęstość sumy jest splotem powyższej gęstości z samą sobą.

Suma dwóch zmiennych ma średnią 0. Gęstość pokazana na rysunku po prawej stronie została przeskalowana o ${\ displaystyle {\ sqrt {2}}}$ , tak że jej odchylenie standardowe wynosi 1.

Ta gęstość jest już gładsza niż oryginał. Występują wyraźne grudki, które odpowiadają przedziałom, w których zdefiniowano pierwotną gęstość.

Gęstość sumy trzech zmiennych .

Funkcja gęstości prawdopodobieństwa sumy trzech wyrazów

Następnie obliczamy gęstość sumy trzech zmiennych niezależnych, z których każda ma powyższą gęstość. Gęstość sumy to splot pierwszej gęstości z drugą.

Suma trzech zmiennych ma średnią 0. Gęstość pokazana na rysunku po prawej stronie została przeskalowana o √ 3 , tak że jej odchylenie standardowe wynosi 1.

Ta gęstość jest jeszcze gładsza niż poprzednia. Na tej figurze trudno dostrzec grudki.

Gęstość sumy czterech zmiennych

Funkcja gęstości prawdopodobieństwa sumy czterech wyrazów

Na koniec obliczamy gęstość sumy czterech zmiennych niezależnych, z których każda ma powyższą gęstość. Gęstość sumy to splot pierwszej gęstości z trzecią (lub drugiej gęstości ze sobą).

Suma czterech zmiennych ma średnią 0. Gęstość pokazana na rysunku po prawej stronie została przeskalowana o √ 4 , tak że jej odchylenie standardowe wynosi 1.

Ta gęstość wydaje się jakościowo bardzo podobna do normalnej gęstości. Okiem nie można odróżnić grudek.

Ilustracja przypadku dyskretnego

Ta sekcja ilustruje centralne twierdzenie graniczne za pomocą przykładu, dla którego obliczenia można szybko wykonać ręcznie na papierze, w przeciwieństwie do bardziej wymagającego obliczeniowo przykładu z poprzedniej sekcji.

Suma wszystkich permutacji o długości 1 wybranych ze zbioru liczb całkowitych 1, 2, 3

Oryginalna funkcja masy prawdopodobieństwa

Załóżmy, że rozkład prawdopodobieństwa dyskretnej zmiennej losowej X przypisuje równe wagi 1, 2 i 3:

{macierz} 1 & {\ mbox {z}} \

Funkcję masy prawdopodobieństwa zmiennej losowej X można przedstawić za pomocą następującego wykresu słupkowego :

Oczywiście w niczym nie przypomina to dzwonowatej krzywej rozkładu normalnego. Porównaj powyższe z poniższymi ilustracjami.

Suma wszystkich permutacji o długości 2 wybranych ze zbioru liczb całkowitych 1, 2, 3

Funkcja masy prawdopodobieństwa sumy dwóch wyrazów

Rozważmy teraz sumę dwóch niezależnych kopii X :

{\ Displaystyle \ lewo \ {{\ rozpocząć {macierz} 1 + 1 & = & 2 \\ 1 + 2 & = & 3 \\ 1 + 3 & = & 4 \\ 2 + 1 & = & 3 \\ 2 + 2 & = & 4 \\ 2+ 3&=&5\\3+1&=&4\\3+2&=&5\\3+3&=&6\end{macierz}}\right\}=\left\{{\begin{matrix}2&{\mbox{ z}}\ {\mbox{prawdopodobieństwo}}\ 1/9\\3&{\mbox{z}}\ {\mbox{prawdopodobieństwo}}\ 2/9\\4&{\mbox{z}}\ {\ mbox{prawdopodobieństwo}}\ 3/9\\5&{\mbox{z}}\ {\mbox{prawdopodobieństwo}}\ 2/9\\6&{\mbox{z}}\ {\mbox{prawdopodobieństwo}}\ 1/9\koniec{macierzy}}\prawo\}}

Funkcję masy prawdopodobieństwa tej sumy można przedstawić w następujący sposób:

To nadal nie wygląda bardzo jak krzywa w kształcie dzwonu, ale podobnie jak krzywa w kształcie dzwonu iw przeciwieństwie do funkcji masy prawdopodobieństwa samego X , jest wyższa w środku niż w dwóch ogonach.

Suma wszystkich permutacji o długości 3 wybranych ze zbioru liczb całkowitych 1, 2, 3

Funkcja masy prawdopodobieństwa sumy trzech wyrazów

Rozważmy teraz sumę trzech niezależnych kopii tej zmiennej losowej:

{\ Displaystyle \ lewo \ {{\ początek {macierz} 1 + 1 + 1 & = & 3 \\ 1 + 1 + 2 & = & 4 \\ 1 + 1 + 3 & = & 5 \\ 1 + 2 + 1 & = & 4 \\ 1 +2+2&=&5\\1+2+3&=&6\\1+3+1&=&5\\1+3+2&=&6\\1+3+3&=&7\\2+1+1&= &4\\2+1+2&=&5\\2+1+3&=&6\\2+2+1&=&5\\2+2+2&=&6\\2+2+3&=&7\\2+ 3+1&=&6\\2+3+2&=&7\\2+3+3&=&8\\3+1+1&=&5\\3+1+2&=&6\\3+1+3&=&7 \\3+2+1&=&6\\3+2+2&=&7\\3+2+3&=&8\\3+3+1&=&7\\3+3+2&=&8\\3+3 +3&=&9\end{macierz}}\right\}=\left\{{\begin{macierz}3&{\mbox{z}}\ {\mbox{prawdopodobieństwo}}\ 1/27\\4&{\ mbox{z}}\ {\mbox{prawdopodobieństwo}}\ 3/27\\5&{\mbox{z}}\ {\mbox{prawdopodobieństwo}}\ 6/27\\6&{\mbox{z}}\ {\mbox{prawdopodobieństwo}}\ 7/27\\7&{\mbox{z}}\ {\mbox{prawdopodobieństwo}}\ 6/27\\8&{\mbox{z}}\ {\mbox{prawdopodobieństwo} }\ 3/27\\9&{\mbox{z}}\ {\mbox{prawdopodobieństwo}}\ 1/27\end{macierz}}\right\}}

Funkcję masy prawdopodobieństwa tej sumy można przedstawić w następujący sposób:

Nie tylko jest to większe w środku niż na ogonach, ale gdy ktoś porusza się w kierunku środka z dowolnego ogona, nachylenie najpierw wzrasta, a następnie maleje, tak jak w przypadku krzywej w kształcie dzwonu.

Stopień jego podobieństwa do krzywej w kształcie dzwonu można określić ilościowo w następujący sposób. Rozważać

Pr( X ₁ + X ₂ + X ₃ ≤ 7) = 1/27 + 3/27 + 6/27 + 7/27 + 6/27 = 23/27 = 0,85185... .

Jak blisko jest to tego, co dałoby normalne przybliżenie? Łatwo zauważyć, że oczekiwana wartość Y = X ₁ + X ₂ + X ₃ wynosi 6, a odchylenie standardowe Y jest pierwiastkiem kwadratowym z 2 . Ponieważ Y ≤ 7 (słaba nierówność) wtedy i tylko wtedy, gdy Y < 8 (ścisła nierówność), używamy poprawki ciągłości i szukamy

{\ Displaystyle {\ mbox {Pr}} (Y \ równoważnik 7,5) = {\ mbox {P}}\left({Y-6 \over {\sqrt {2}}}\leq {7,5-6 \over {\sqrt {2}}}\right)={\mbox{Pr}}(Z \leq 1,0606602\kropek )=0,85558\kropek}

gdzie Z ma standardowy rozkład normalny. Różnica między 0,85185… a 0,85558… wydaje się niezwykle mała, jeśli weźmie się pod uwagę, że liczba niezależnych zmiennych losowych, które zostały dodane, wynosiła tylko trzy.

Funkcja masy prawdopodobieństwa sumy 1000 wyrazów

Poniższy rysunek przedstawia wynik symulacji na przykładzie przedstawionym na tej stronie. Ekstrakcja z rozkładu jednorodnego jest powtarzana 1000 razy, a wyniki są sumowane.

Ponieważ symulacja oparta jest na metodzie Monte Carlo , proces jest powtarzany 10 000 razy. Wyniki pokazują, że rozkład sumy 1000 jednorodnych ekstrakcji bardzo dobrze przypomina krzywą w kształcie dzwonu.

Linki zewnętrzne