Klastrowanie strumieni danych
W informatyce grupowanie strumieni danych definiuje się jako grupowanie danych, które napływają w sposób ciągły, takich jak zapisy rozmów telefonicznych, dane multimedialne, transakcje finansowe itp. Klastrowanie strumieni danych jest zwykle badane jako algorytm przesyłania strumieniowego , a celem jest, biorąc pod uwagę sekwencję punktów, skonstruować dobre klastrowanie strumienia przy użyciu niewielkiej ilości pamięci i czasu.
Historia
Klastrowanie strumieni danych przyciągnęło ostatnio uwagę nowych aplikacji, które wymagają przesyłania dużych ilości danych strumieniowych. W przypadku grupowania k-średnie jest szeroko stosowaną heurystyką, ale opracowano również alternatywne algorytmy, takie jak k-medoids , CURE i popularny [ potrzebne źródło ] BIRCH . W przypadku strumieni danych jeden z pierwszych wyników pojawił się w 1980 r., ale model został sformalizowany w 1998 r.
Definicja
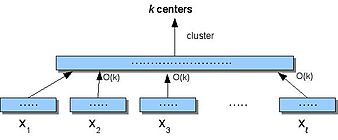
Problem klastrowania strumieni danych definiuje się jako:
Wejście: ciąg n punktów w przestrzeni metrycznej i liczba całkowita k . Wynik: k centrów w zbiorze n punktów, aby zminimalizować sumę odległości od punktów danych do ich najbliższych centrów skupień.
To jest strumieniowa wersja problemu k-mediany.
Algorytmy
STRUMIEŃ
STREAM jest algorytmem grupowania strumieni danych opisanym przez Guha, Mishrę, Motwaniego i O'Callaghana, który osiąga stałe przybliżenie czynnikowe dla problemu k-Median w jednym przebiegu i przy użyciu małej przestrzeni.
Twierdzenie — STREAM może rozwiązać problem k -mediany w strumieniu danych w jednym przebiegu, z czasem O ( n 1+ e ) i przestrzenią θ ( n ε ) aż do współczynnika 2 O(1/ ) , e gdzie n liczba punktów i .
Aby zrozumieć STREAM, pierwszym krokiem jest pokazanie, że klastrowanie może odbywać się na małej przestrzeni (nie dbając o liczbę przebiegów). Small-Space to algorytm typu „dziel i zwyciężaj” , który dzieli dane S , na , grupuje każdy z nich (przy użyciu k -średnich), a następnie grupuje centra.
Algorytm mała przestrzeń (S)
- Podziel S na rozłączne części .
- Dla każdego ja znajdź centra _ _ Przypisz każdemu punktowi X i jego najbliższy środek.
- Niech ' będzie centrami uzyskanymi w (2), gdzie każde centrum liczbą przypisanych mu
- Cluster X', aby znaleźć centra k .
uruchomimy bikryteria - algorytm aproksymacji który daje co najwyżej ak mediany kosztem co najwyżej b razy optymalne rozwiązanie k-mediany, aw kroku uruchom algorytm aproksymacji c , a następnie współczynnik aproksymacji algorytmu Small-Space() wynosi . Możemy również uogólnić Małą Przestrzeń tak, aby rekurencyjnie wywoływała się i razy na kolejno mniejszym zbiorze ważonych centrów i osiągała stałe współczynnikowe przybliżenie problemu k -mediany.
na tym, że liczba podzbiorów które dzielimy jest ograniczona, ponieważ musi przechowywać w pamięci mediany pośrednie w X . Tak więc, jeśli M jest rozmiarem pamięci, musimy podzielić S na podzbiory tak, aby każdy podzbiór mieścił się w pamięci ( i aby ważony centra również mieszczą się w pamięci, . Ale taki nie zawsze może istnieć.
Algorytm STREAM rozwiązuje problem przechowywania median pośrednich i osiąga lepsze wymagania dotyczące czasu działania i przestrzeni. Algorytm działa w następujący sposób:
- Wprowadź pierwsze m punktów; algorytmu przedstawionego w zmniejsz je do ( 2 k )
- Powtarzaj powyższe, aż zobaczymy m 2 /(2 k ) oryginalnych punktów danych. Mamy teraz m median pośrednich.
- Korzystając z lokalnego algorytmu wyszukiwania , zgrupuj te m median pierwszego poziomu w 2 k median drugiego poziomu i kontynuuj.
- Ogólnie rzecz biorąc, utrzymuj co najwyżej m median poziomu- i i widząc m wygeneruj 2 k median poziomu- i + 1, z wagą nowej mediany jako sumą wag przypisanych jej median pośrednich.
- Kiedy widzieliśmy wszystkie oryginalne punkty danych, grupujemy wszystkie pośrednie mediany w k końcowych median, używając pierwotnego algorytmu dualnego.
Inne algorytmy
Inne dobrze znane algorytmy używane do grupowania strumieni danych to:
- BIRCH : buduje hierarchiczną strukturę danych, aby stopniowo grupować przychodzące punkty przy użyciu dostępnej pamięci i minimalizując ilość wymaganych wejść/wyjść. Złożoność algorytmu jest taka, jeden przebieg wystarcza, aby uzyskać dobre skupienie (chociaż wyniki można poprawić, dopuszczając
- COBWEB : to przyrostowa technika klastrowania, która utrzymuje hierarchiczny model klastrowania w formie drzewa klasyfikacyjnego . Dla każdego nowego punktu COBWEB schodzi w dół drzewa, aktualizuje węzły po drodze i szuka najlepszego węzła, na którym można umieścić punkt (za pomocą funkcji użyteczności kategorii ).
- C2ICM: buduje płaską partycjonowaną strukturę klastrów, wybierając niektóre obiekty jako nasiona/inicjatory klastra, a nie-ziarno jest przypisywane do ziarna, które zapewnia największe pokrycie, dodanie nowych obiektów może wprowadzić nowe nasiona i sfałszować niektóre istniejące stare nasiona, podczas przyrostowego grupowanie nowych obiektów, a członkowie sfałszowanych klastrów są przypisywani do jednego z istniejących nowych/starych nasion.
- CluStream: wykorzystuje mikroklastry, które są czasowymi rozszerzeniami wektora cech klastra BIRCH , dzięki czemu może zdecydować, czy mikroklaster może zostać utworzony na nowo, połączony lub zapomniany na podstawie analizy kwadratowej i liniowej sumy obecnych mikroklastrów punktów danych i znaczników czasu, a następnie w dowolnym momencie można generować makroklastry poprzez grupowanie tych mikroklastrów przy użyciu algorytmu klastrowania offline, takiego jak K-Means , uzyskując w ten sposób końcowy wynik klastrowania.