Konstrukcja Thompsona

W informatyce algorytm konstrukcyjny Thompsona , zwany także algorytmem McNaughtona – Yamady – Thompsona , jest metodą przekształcania wyrażenia regularnego w równoważny niedeterministyczny automat skończony (NFA). Ten NFA może służyć do dopasowywania ciągów znaków do wyrażenia regularnego. Algorytm ten jest przypisywany Kenowi Thompsonowi .

Wyrażenia regularne i niedeterministyczne automaty skończone to dwie reprezentacje języków formalnych . Na przykład do przetwarzania tekstu używają wyrażeń regularnych do opisywania zaawansowanych wzorców wyszukiwania, ale NFA lepiej nadają się do wykonywania na komputerze. Dlatego ten algorytm ma praktyczne znaczenie, ponieważ może kompilować wyrażenia regularne w NFA. Z teoretycznego punktu widzenia algorytm ten jest częścią dowodu na to, że oba akceptują dokładnie te same języki, czyli języki regularne .

NFA można uczynić deterministycznym za pomocą konstrukcji powerset , a następnie zminimalizować , aby uzyskać optymalny automat odpowiadający danemu wyrażeniu regularnemu. Jednak NFA można również interpretować bezpośrednio .

Aby zdecydować, czy dwa podane wyrażenia regularne opisują ten sam język, każde z nich można przekształcić w równoważny minimalny deterministyczny automat skończony za pomocą konstrukcji Thompsona, konstrukcji powerset i minimalizacji DFA . Jeśli i tylko wtedy, gdy wynikowe automaty zgadzają się ze zmianą nazw stanów, języki wyrażeń regularnych są zgodne.

Algorytm

Algorytm działa rekurencyjnie , dzieląc wyrażenie na składowe podwyrażenia, z których NFA zostanie zbudowane przy użyciu zestawu reguł. Dokładniej, z wyrażenia regularnego $E$ , uzyskany automat $A$ z funkcją przejścia $Δ$ ^{[ wymagane wyjaśnienie ]} zachowuje następujące właściwości:

$A$ ma dokładnie jeden stan początkowy $q 0$ , który nie jest dostępny z żadnego innego stanu. Oznacza to, że dla dowolnego stanu $q$ i dowolnej litery $za$ , ${\ Displaystyle \ Delta (q, a)}$ nie zawiera $q 0$ .
$A$ ma dokładnie jeden stan końcowy $q f$ , który nie jest współdostępny z żadnego innego stanu. To znaczy dla dowolnej litery $za$ , ${\ Displaystyle \ Delta (q_ {f}, a) = \ pusty zbiór}$ .
Niech $c$ będzie liczbą konkatenacji wyrażenia regularnego $E$ i niech $s$ będzie liczbą symboli poza nawiasami — czyli $|$ , $*$ , $a$ i $ε$ . Wtedy liczba stanów $A$ wynosi $2 s - c$ (liniowa w rozmiarze $E$ ).
Liczba przejść wychodzących z dowolnego stanu wynosi co najwyżej dwa.
Ponieważ NFA o $m$ stanach i co najwyżej $e$ przejściach z każdego stanu może dopasować łańcuch o długości $n$ w czasie $O (emn)$ , NFA Thompsona może wykonać dopasowywanie wzorców w czasie liniowym, zakładając alfabet o stałym rozmiarze. ^{[ potrzebne lepsze źródło ]}

Zasady

Następujące zasady są przedstawione zgodnie z Aho et al. (2007), s. 122. Poniżej N ( s ) i N ( t ) są odpowiednio NFA podwyrażeń s i t .

Puste wyrażenie ε jest konwertowane na

jest symbol a wejściowego alfabetu

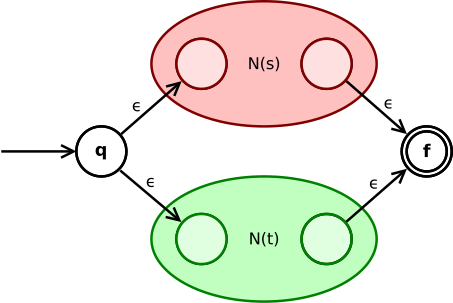
Wyrażenie sumy s | t jest konwertowane na

Stan q przechodzi przez ε do stanu początkowego N ( s ) lub N ( t ). Ich stany końcowe stają się stanami pośrednimi całego NFA i łączą się poprzez dwa przejścia ε w stan końcowy NFA.

Wyrażenie konkatenacji st jest konwertowane na

Stan początkowy N ( s ) jest stanem początkowym całego NFA. Stan końcowy N ( s ) staje się stanem początkowym N ( t ). Stan końcowy N ( t ) jest końcowym stanem całego NFA.

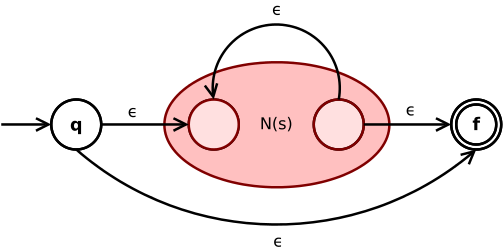
Wyrażenie gwiazdy Kleene s * jest konwertowane ^na

Przejście ε łączy początkowy i końcowy stan NFA z pod-NFA N ( s ) pomiędzy nimi. Kolejne przejście ε z wewnętrznego stanu końcowego do wewnętrznego stanu początkowego N ( s ) pozwala na powtórzenie wyrażenia s zgodnie z operatorem gwiazdy.

Wyrażenie w nawiasach ( s ) jest konwertowane na samo N ( s ).

Dzięki tym regułom, używając pustych wyrażeń i reguł symboli jako przypadków bazowych, można udowodnić za pomocą indukcji matematycznej , że dowolne wyrażenie regularne można przekształcić w równoważny NFA.

Przykład

Podano teraz dwa przykłady, mały nieformalny z wynikiem i większy z zastosowaniem algorytmu krok po kroku.

Mały przykład

Przykład (ε|a*b) z wykorzystaniem konstrukcji Thompsona, krok po kroku

Poniższy rysunek przedstawia wynik konstrukcji Thompsona na (ε|a*b) . Fioletowy owal odpowiada a , turkusowy owal odpowiada a* , zielony owal odpowiada b , pomarańczowy owal odpowiada a*b , a niebieski owal odpowiada ε .

Zastosowanie algorytmu

NFA uzyskany z wyrażenia regularnego (0|(1(01*(00)*0)*1)*)*

Jako przykład, rysunek pokazuje wynik algorytmu konstrukcji Thompsona na wyrażeniu regularnym (0|(1(01*(00)*0)*1)*)* oznaczającym zbiór liczb binarnych będących wielokrotnościami 3:

{ε, „0”, „00”, „11”, „000”, „011”, „110”, „0000”, „0011”, „0110”, „1001”, „1100”, „1111” , "00000", ... }.

Prawa górna część pokazuje strukturę logiczną (drzewo składni) wyrażenia, z "." oznaczający konkatenację (zakłada się, że ma zmienną arity); podwyrażenia są nazywane a - q dla celów informacyjnych. Lewa część przedstawia niedeterministyczny automat skończony wynikający z algorytmu Thompsona, ze wejścia i wyjścia każdego podwyrażenia w kolorze magenta i cyjan odpowiednio. Dla jasności pominięto ε jako etykietę przejścia — przejścia nieoznaczone są w rzeczywistości przejściami ε. Stan wejścia i wyjścia odpowiadający wyrażeniu głównemu q jest odpowiednio stanem początkowym i akceptującym automatu.

Kroki algorytmu są następujące:

q :	zacznij konwertować wyrażenie gwiazdy Kleene									`(0\|(1(01(00)0)1))*`
	b :	rozpocznij konwersję wyrażenia unii								`0\|(1(01(00)0)1)`
		za :	przekonwertować symbol							`0`
		p :	zacznij konwertować wyrażenie gwiazdy Kleene							`(1(01(00)0)1)`
			re :	rozpocznij konwersję wyrażenia konkatenacyjnego						`1(01(00)0)*1`
				c :	przekonwertować symbol					`1`
				n :	zacznij konwertować wyrażenie gwiazdy Kleene					`(01(00)0)*`
					fa :	rozpocznij konwersję wyrażenia konkatenacyjnego				`01(00)0`
						e :	przekonwertować symbol			`0`
						godzina :	zacznij konwertować wyrażenie gwiazdy Kleene			`1*`
							g :	przekonwertować symbol		`1`
						godzina :	skończyłem konwertować wyrażenie gwiazdy Kleene			`1*`
						ja :	zacznij konwertować wyrażenie gwiazdy Kleene			`(00)*`
							j :	rozpocznij konwersję wyrażenia konkatenacyjnego		`00`
								ja :	przekonwertować symbol	`0`
								k :	przekonwertować symbol	`0`
							j :	zakończono konwersję wyrażenia konkatenacyjnego		`00`
						ja :	skończyłem konwertować wyrażenie gwiazdy Kleene			`(00)*`
						m :	przekonwertować symbol			`0`
					fa :	zakończono konwersję wyrażenia konkatenacyjnego				`01(00)0`
				n :	skończyłem konwertować wyrażenie gwiazdy Kleene					`(01(00)0)*`
				o :	przekonwertować symbol					`1`
			re :	zakończono konwersję wyrażenia konkatenacyjnego						`1(01(00)0)*1`
		p :	skończyłem konwertować wyrażenie gwiazdy Kleene							`(1(01(00)0)1)`
	b :	zakończono konwersję wyrażenia unii								`0\|(1(01(00)0)1)`
q :	skończyłem konwertować wyrażenie gwiazdy Kleene									`(0\|(1(01(00)0)1))*`

Równoważny minimalny automat deterministyczny pokazano poniżej.

Związek z innymi algorytmami

Thompsona jest jednym z kilku algorytmów konstruowania NFA z wyrażeń regularnych; wcześniejszy algorytm został podany przez McNaughtona i Yamadę. W przeciwieństwie do konstrukcji Thompsona, algorytm Kleene'a przekształca automat skończony w wyrażenie regularne.

Algorytm konstrukcji Głuszkowa jest podobny do konstrukcji Thompsona, po usunięciu przejść ε.

Smyczki
Metryka ciągu	Przybliżone dopasowanie ciągów Algorytm bitapowy Odległość Damerau-Levenshteina Edytuj odległość Dopasowanie wzorca Gestalt Odległość Hamminga Odległość Jaro-Winklera Odległość Lee Automat Levenshteina Odległość Levenshteina Algorytm Wagnera-Fischera
Algorytm przeszukiwania ciągów znaków	Algorytm Apostolico – Giancarlo Algorytm przeszukiwania łańcuchów Boyera-Moore'a Algorytm Boyera-Moore'a-Horspoola Algorytm Knutha – Morrisa – Pratta Algorytm Rabina-Karpa
Wyszukiwanie wielu ciągów	Aho-Corasick Algorytm Commentza-Waltera
Wyrażenie regularne	Porównanie silników wyrażeń regularnych Zwykła gramatyka Konstrukcja Thompsona Niedeterministyczny automat skończony
Wyrównanie sekwencji	Algorytm Hirschberga Algorytm Needlemana-Wunscha Algorytm Smitha-Watermana
Struktura danych	DAFSA Tablica sufiksów Automat sufiksowy Drzewo sufiksów Uogólnione drzewo sufiksów Lina Trójskładnikowe drzewo wyszukiwania Spróbuj
Inny	Rozbiór gramatyczny zdania Dopasowanie wzorca Skompresowane dopasowanie wzorca Najdłuższy wspólny podciąg Najdłuższy wspólny podciąg Eksploracja wzorców sekwencyjnych Sortowanie