Logarytm Gaussa

W matematyce logarytmy dodawania i odejmowania lub logarytmy Gaussa można wykorzystać do znalezienia logarytmów sumy i różnicy pary wartości, których logarytmy są znane, bez znajomości samych wartości.

Ich matematyczne podstawy sięgają czasów Zecchiniego Leonellego i Carla Friedricha Gaussa na początku XIX wieku.

Funkcje dla s ${\ Displaystyle s_ {b} (z)}$ i ${\ Displaystyle d_ {b} (z)}$${\ Displaystyle b = e$ .

Operacje dodawania i odejmowania można obliczyć ze wzoru:

${\ Displaystyle \ log _ {b} (| X | + | Y |) = x + s_ {b} (yx) }$

${\ Displaystyle \ log _ {b} (|| X | - | Y||) = x + d_ {b}(yx)}$

gdzie ${\ Displaystyle x = \ log _ {b} (X)}$ y $\ Displaystyle y = \ log _ {b} (Y)}$ , funkcja „suma” jest zdefiniowana przez ${\ Displaystyle s_ {b} (z) = \ log _ {b} (1 + b ^ {z})}$ , a funkcja „różnica” przez ${\ Displaystyle d_ {b} (z) = \ log _ {b} (| 1-b ^ {z} |)}$ . Funkcje ${\ Displaystyle$ re $)}$ są również znane jako logarytmy .

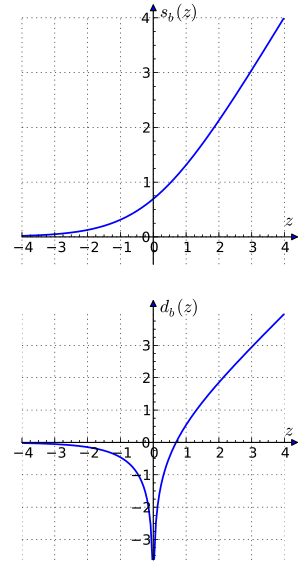
Dla logarytmów naturalnych z istnieją następujące tożsamości z funkcjami hiperbolicznymi : ${\ displaystyle b = e}$

${\ Displaystyle s_ {e} (z) = \ ln 2 + {\ Frac {z} {2}} + \ ln \ lewo (\ cosh {\ Frac {z} {2}} \ prawo)}$

${\ Displaystyle d_ {e} (z) = \ ln 2 + {\ Frac {z} {2}} + \ ln \ lewo | \ sinh {\ Frac {z} {2}} \ prawo |}$

To pokazuje, że $, w którym wszystkie wyrażenia oprócz pierwszego są racjonalne$ Taylora , a wszystkie wyrażenia nieparzyste oprócz liniowego wynoszą zero.

Uproszczenie mnożenia, dzielenia, pierwiastków i potęg jest równoważone kosztem oceny tych funkcji pod kątem dodawania i odejmowania.

Zobacz też

• Działanie Softplus w sieciach neuronowych
• logarytm Zacha
• Tabela logarytmów
• System liczb logarytmicznych (LNS)

Dalsza lektura

•   Stark, Bruce D. (1997) [1995]. Tabele Starka do obliczania odległości księżycowej i znajdowania czasu uniwersalnego przez obserwację sekstansową, w tym wygodny sposób na wyostrzenie umiejętności nawigacji na niebie podczas pobytu na lądzie (wyd. 2). Publikacje Gwiezdnej Ścieżki. ISBN 978-0914025214 . 091402521X . Źródło 2015-12-02 . (Uwaga. Zawiera tabelę logarytmów Gaussa lg (1+10 ^−x ).)
• Kalivoda, styczeń (2003-07-30). „Bruce Stark - Tabele do obliczania odległości księżycowej i znajdowania GMT przez obserwację sekstantu (1995, 1997)” (recenzja). Praga, Republika Czeska. Zarchiwizowane od oryginału w dniu 12.01.2004 . Źródło 2015-12-02 . …] Bruce Stark […] posługuje się logarytmami gaussowskimi, które pozwalają pozostać w świecie logarytmów przez cały czas obliczeń i przekształcić dodawanie liczb naturalnych w dodawanie i odejmowanie ich logarytmów wspólnych i specjalnych za pomocą specjalnej tablicy . Jest to o wiele łatwiejsze niż przekonwertowanie kłód na ich naturalne wartości, dodanie ich i ponowne przekształcenie w kłody. Co więcej, logarytmy gaussowskie zapewniają większą dokładność wyników niż tradycyjna metoda obliczeniowa i pomagają 5-cyfrowym wartościom logarytmicznym zapewnić wystarczającą dokładność dla tej metody. […] Użycie „gaussów” przez Bruce'a jest oryginalne w dziedzinie nawigacji. Nie znam innego przykładu wykorzystania ich przez marynarzy czy lotników - poza sowieckimi nawigatorami, którzy mieli gaussy w swoich standardowych układach stołowych do ok. 1960. […] harsine , który nie był dopuszczony do sowieckiej praktyki nawigacyjnej. […] Gaussowie pokojowo współpracują z haversinami w racjonalizowaniu procedury LD […] [1] [2]
• Kremer, Hermann (2002-08-29). "Gauss'sche Additionslogarithmen feiern 200. Geburtstag" . de.sci.mathematik (w języku niemieckim). Zarchiwizowane od oryginału w dniu 2018-07-07 . Źródło 2018-07-07 .
• Kühn, Klaus (2008). „CF Gauß und die Logarithmen” (PDF) (w języku niemieckim). Alling-Biburg, Niemcy. Zarchiwizowane (PDF) od oryginału w dniu 14.07.2018 r . Źródło 2018-07-14 .