Dekrement logarytmiczny

Dekrement logarytmiczny można otrzymać np. jako ln( x ₁ / x ₃ ).

Dekrement logarytmiczny $,$ jest używany do znalezienia tłumienia niedotłumionego systemu w dziedzinie czasu.

Metoda dekrementacji logarytmicznej staje się coraz mniej dokładna, gdy współczynnik tłumienia wzrasta powyżej około 0,5; nie ma to w ogóle zastosowania dla współczynnika tłumienia większego niż 1,0, ponieważ układ jest przetłumiony .

metoda

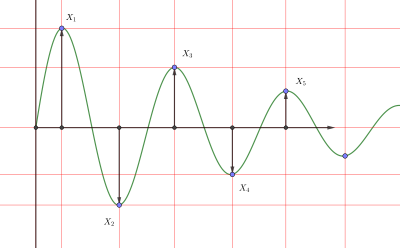
Dekrement logarytmiczny definiuje się jako logarytm naturalny stosunku amplitud dowolnych dwóch kolejnych pików:

${\ Displaystyle \ delta = {\ Frac {1} {n}} \ ln {\ Frac {x (t)} {x (t + nT) )}}}$

gdzie x ( t ) to przeregulowanie (amplituda - wartość końcowa) w czasie t , a x ( t + nT ) to przeregulowanie piku oddalonego o n okresów, gdzie n to dowolna liczba całkowita kolejnych dodatnich pików.

Współczynnik tłumienia jest następnie obliczany na podstawie logarytmicznego dekrementu:

${\ Displaystyle \ zeta = {\ Frac {\ delta}} {\ sqrt {4 \ pi ^ {2} + \ delta ^ {2}}}}}$

Zatem dekrement logarytmiczny pozwala również na ocenę współczynnika Q systemu:

${\ Displaystyle Q = {\ Frac {1} {2 \ zeta}}}$

${\ styl wyświetlania Q = {\ frac {1}{2}}{\sqrt {1+\lewo ({\frac {n2\pi}} {\ln {\frac {x(t)}{x(t+nT)} }}}\prawo)^{2}}}}$

Współczynnik tłumienia można następnie wykorzystać do znalezienia częstotliwości drgań własnych ω _n układu na podstawie tłumionej częstotliwości drgań własnych ω _d :

${\ Displaystyle \ omega _ {d} = {\ Frac {2 \ pi} {T}}}$

${\ Displaystyle \ omega _ {n} = {\ frac {\omega _{d}}{\sqrt {1-\zeta ^{2}}}}}$

gdzie T , okres przebiegu, jest czasem między dwoma kolejnymi szczytami amplitudy niedotłumionego układu.

Uproszczona odmiana

Współczynnik tłumienia można znaleźć dla dowolnych dwóch sąsiednich pików. Ta metoda jest używana, gdy n = 1 i wywodzi się z powyższej metody ogólnej:

${\ Displaystyle \ zeta = {\ Frac {1} {\ sqrt {1 + \ lewo ({\ Frac {2 \ pi}} {\ ln \ lewo({\frac {x_{0}}{x_{1}}}\prawo)}}\prawo)^{2}}}}}$

₀ gdzie x i x ₁ to amplitudy dowolnych dwóch kolejnych pików.

Dla systemu, w którym (niezbyt blisko reżimu krytycznie tłumionego, gdzie $ζ$$\ około 1$ )

${\ Displaystyle \ zeta \ około {\ Frac {\ ln \ lewo ({\ Frac {x_ {0}}} {x_ {1}}} \ prawej)} {2 \ Liczba Pi }}}$

Metoda przeregulowania ułamkowego

Metoda ułamkowego przeregulowania może być użyteczna dla współczynników tłumienia między około 0,5 a 0,8. Ułamkowe przeregulowanie OS to:

${\ Displaystyle \ operatorname {OS} = {\ Frac {x_ {p} -x_ {f}} {x_ {f}}}}$

gdzie x _p jest amplitudą pierwszego piku odpowiedzi skokowej, a x _f jest amplitudą ustalania. Wtedy współczynnik tłumienia wynosi

${\ Displaystyle \ zeta = {\ Frac {1} {\ sqrt {1 + \ lewo ({\ Frac {\ pi}} {\ ln (\ operatorname { OS} )}}\right)^{2}}}}}$

Zobacz też

• Współczynnik tłumienia

•   Inman, Daniel J. (2008). Wibracje inżynierskie . Upper Saddle, NJ: Pearson Education, Inc., s. 43–48. ISBN 978-0-13-228173-7 .