Logika wielu sortowań

Logika z wieloma sortowaniami może formalnie odzwierciedlać naszą intencję, by nie traktować wszechświata jako jednorodnego zbioru obiektów, ale podzielić go w sposób podobny do typów w programowaniu typu . Zarówno funkcjonalne, jak i asertywne „ części mowy ” w języku logiki odzwierciedlają ten typowy podział wszechświata, nawet na poziomie składni: podstawianie i przekazywanie argumentów może odbywać się tylko odpowiednio, z poszanowaniem „rodzajów”.

Istnieją różne sposoby sformalizowania wspomnianej powyżej intencji; logika wielosortowana to dowolny pakiet informacji, który ją spełnia. W większości przypadków podaje się:

zestaw rodzajów, S
odpowiednie uogólnienie pojęcia podpisu , aby móc obsłużyć dodatkowe informacje towarzyszące sortowaniu.

Dziedzina dyskursu dowolnej struktury tej sygnatury jest następnie dzielona na rozłączne podzbiory, po jednym dla każdego rodzaju.

Przykład

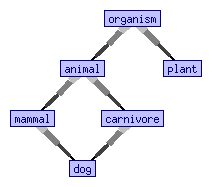
Podczas rozumowania na temat organizmów biologicznych warto rozróżnić dwa rodzaje: ${\ displaystyle \ operatorname {roślina}}$ i ${\ displaystyle \ operatorname {zwierzę}}$ . gdy funkcja ${\ Displaystyle \ operatorname {matka} \ okrężnica \ operatorname {zwierzę} \ do \ operatorname {zwierzę}}$ ma sens, podobna funkcja ${\ displaystyle \mathrm {matka} \colon \mathrm {roślina} \to \mathrm {roślina} }$ zazwyczaj nie. wielosortowania ${\ Displaystyle \ operatorname {matka} (\ operatorname {lassie} )}$ , ale aby odrzucić terminy takie jak ${\ Displaystyle \mathrm {mother} (\mathrm {my\_favorite\_oak} )}$ jako składniowo źle sformułowane.

Algebraizacja

Algebraizacja logiki z wieloma sortowaniami została wyjaśniona w artykule Caleiro i Gonçalvesa, który uogólnia abstrakcyjną logikę algebraiczną na przypadek z wieloma sortowaniami, ale może być również użyty jako materiał wprowadzający.

Logika uporządkowana według kolejności

Przykładowa hierarchia sortowania

Podczas gdy logika posortowana według wielu wymaga, aby dwa odrębne rodzaje miały rozłączne zbiory wszechświatów, logika posortowana według kolejności pozwala na zadeklarowanie $displaystyle$ jako podsortu innego rodzaju $s_ {2}}$ $_$ pisząc składnię W powyższym przykładzie z biologii pożądane jest zadeklarowanie

{\ Displaystyle {\ tekst {pies}} \ subseteq {\ tekst {mięsożerca}}}

,

{\ Displaystyle {\ tekst {pies}} \ subseteq {\ tekst {ssak}}}

,

{\ Displaystyle {\ tekst {mięsożerca}} \ subseteq {\ tekst {zwierzę}}}

,

{\ Displaystyle {\ tekst {ssak}} \ subseteq {\ tekst {zwierzę}}}

,

{ \ Displaystyle {\ tekst {zwierzę}} \ subseteq {\ tekst {organizm}}}

,

{\ Displaystyle {\ tekst {roślina}} \ subseteq {\ tekst {organizm}}}

,

i tak dalej; por. zdjęcie.

Wszędzie tam, gdzie wymagany jest jakiś termin $tego$ można podać termin dowolnego podrodzaju $)$ zasada podstawienia Liskowa . Na przykład, zakładając deklarację funkcji ${\ Displaystyle {\ tekst {matka}}: {\ tekst {zwierzę}} \ longrightarrow {\ tekst {zwierzę}}}$ i stałą deklarację ${\ displaystyle {\text{lassie}}:{\text{pies}}}$ , termin ${\ Displaystyle {\ text {mother}} ({\ text {lassie}})}$ jest całkowicie poprawne i ma sortowanie ${\ displaystyle {\ text {zwierzę}}}$ . W celu dostarczenia informacji, że matką psa jest z kolei pies, kolejna deklaracja ${\ Displaystyle {\ tekst {matka}}: {\ tekst {pies}} \ longrightarrow {\ tekst {pies} }}}$ może zostać wydane; nazywa się to przeciążaniem funkcji , podobnie jak przeciążanie w językach programowania .

Logikę uporządkowaną $i$ $kolejności$ można przetłumaczyć na logikę nieposortowaną, dla ${\ Displaystyle \ forall x (p_ {i} (x) \ rightarrow p_ {j} (x))}$ dla każdej deklaracji podsortowania ${\ Displaystyle s_ {i} \ subseteq s_ {j}}$ . Podejście odwrotne powiodło się w zautomatyzowanym dowodzeniu twierdzeń: w 1985 roku Christoph Walther mógł rozwiązać ówczesny problem wzorcowy, tłumacząc go na logikę posortowaną rzędem, a tym samym sprowadzając go do rzędu wielkości, ponieważ wiele predykatów jednoargumentowych zamieniło się w sortowania.

Aby włączyć logikę posortowaną według kolejności do automatycznego dowodzenia twierdzeń opartego na klauzulach, niezbędny jest odpowiedni algorytm unifikacyjny posortowany według kolejności , który dla dowolnych dwóch zadeklarowanych sortowań wymaga $}$ ${\ displaystyle s_ {1}, s_ {2$ } ich przecięcie $i$ ma zostać zadeklarowane: jeśli i $Displaystyle x_ {1}}$ $Displaystyle x_ {2} }$ są zmiennymi typu ${\ Displaystyle s_ {1}}$ i ${\ Displaystyle s_ {2}}$ odpowiednio równanie ${\ Displaystyle x_ {1} {\ stackrel {?} {=}} \, x_ {2}}$ ma rozwiązanie ${\ Displaystyle \ {x_ {1} = x, \; x_ {2} = x \}}$ , gdzie ${\ Displaystyle x: s_ {1} \ cap s_ {2}}$ .

Smolka uogólnił logikę sortowaną według kolejności, aby umożliwić polimorfizm parametryczny . W jego ramach deklaracje podsortowania są propagowane do wyrażeń typu złożonego. można zadeklarować parametryczną $jest$ parametrem, jak w szablonie C++ ), od $displaystyle X$ deklaracja podsortowania ${\ Displaystyle {\ tekst {int}} \ subseteq {\ tekst {float}}}$ relacji ${\ Displaystyle {\ text {list}} ({\ text {int}}) \ subseteq {\ text {list}} ({\ text {float}})} jest automatycznie wywnioskowany, co$ oznacza że każda lista liczb całkowitych jest również listą liczb zmiennoprzecinkowych.

Schmidt-Schauß uogólnił logikę sortowania według kolejności, aby umożliwić deklaracje terminów. Jako przykład, zakładając deklaracje podsortowania ${\ Displaystyle {\ tekst {parzyste}} \ subseteq {\ tekst {int}}}$ $\ Displaystyle {\ tekst {nieparzyste}} \ subseteq {\ tekst { int}}}$ ⊆ , deklaracja terminu, taka jak ${\ Displaystyle \ forall i: {\ tekst {int}}. \; (i + i): {\ tekst {parzysty}}}$ pozwala zadeklarować właściwość dodawania liczb całkowitych, której nie można wyrazić zwykłym przeciążeniem.

Zobacz też

Wczesne artykuły na temat logiki wielosortowanej obejmują:

Wang, Hao (1952). „Logika wielu sortowanych teorii”. Dziennik logiki symbolicznej . 17 (2): 105–116. doi : 10.2307/2266241 . JSTOR 2266241 . , zebrane w autorskiej książce Computation, Logic, Philosophy. Zbiór esejów , Pekin: Science Press; Dordrecht: Kluwer Academic, 1990.
Gilmore, PC (1958). „Dodatek do„ Logiki wielu posortowanych teorii ” ” (PDF) . Compositio Mathematica . 13 : 277–281.
A. Oberschelp (1962). "Untersuchungen zur mehrsortigen Quantorenlogik" . Mathematische Annalen . 145 (4): 297–333. doi : 10.1007/bf01396685 . S2CID 123363080 . Zarchiwizowane od oryginału w dniu 2015-02-20 . Źródło 2013-09-11 .
F. Jeffrey Pelletier (1972). „Kwantyfikacja sortowania i kwantyfikacja ograniczona” (PDF) . Studia filozoficzne . 23 (6): 400–404. doi : 10.1007/bf00355532 . S2CID 170303654 .

Linki zewnętrzne

„Logika wielu sortowań”, pierwszy rozdział w notatkach do wykładów na temat procedur decyzyjnych autorstwa Calogero G. Zarby