Mączna maszyna

W teorii obliczeń maszyna Mealy'ego jest maszyną o skończonych stanach , której wartości wyjściowe są określone zarówno przez jej aktualny stan , jak i bieżące wejścia. Kontrastuje to z maszyną Moore'a , której wartości wyjściowe są określane wyłącznie przez jej aktualny stan. Maszyna Mealy'ego jest deterministycznym przetwornikiem stanu skończonego : dla każdego stanu i wejścia możliwa jest co najwyżej jedna zmiana.

Historia

Maszyna Mealy została nazwana na cześć George'a H. Mealy'ego , który przedstawił tę koncepcję w artykule z 1955 r. „A Method for Synthesizing Sequential Circuits”.

Definicja formalna

$_$ Mealy'ego - _

skończony zbiór stanów ${\ displaystyle S$ }
stan początkowy (zwany także stanem początkowym), $S}$ jest elementem $\ displaystyle$
skończony zbiór zwany alfabetem wejściowym ${\ displaystyle \ Sigma}$
skończony zbiór zwany alfabetem wyjściowym ${\ Displaystyle \ Lambda}$
funkcja przejścia odwzorowująca pary stanu i symbol wejściowy na odpowiedni następny stan ${\ displaystyle T: S \ razy \ Sigma \ rightarrow S} .$
$odwzorowująca$ wyjściowa pary stanu i symbol

W niektórych sformułowaniach funkcje przejścia i wyjścia są połączone w jedną funkcję ${\ Displaystyle T: S \ razy \ Sigma \ rightarrow S \ razy \ Lambda$ }

Porównanie maszyn Mealy'ego i maszyn Moore'a

Maszyny Mealy mają zwykle mniej stanów:
- Różne wyjścia na łukach ( n ² ) zamiast stanów ( n ).
Maszyny Moore'a są bezpieczniejsze w użyciu:
- Wyjścia zmieniają się na zboczu zegara (zawsze jeden cykl później).
- W maszynach Mealy zmiana wejścia może spowodować zmianę wyjścia, gdy tylko logika zostanie wykonana - duży problem, gdy dwie maszyny są ze sobą połączone - asynchroniczne sprzężenie zwrotne może wystąpić, jeśli jedna nie jest ostrożna.
Mączne maszyny reagują szybciej na dane wejściowe:
- Reaguj w tym samym cyklu – nie muszą czekać na zegar.
- W maszynach Moore'a może być konieczne więcej logiki do dekodowania stanu na wyjścia - więcej opóźnień bramek po zboczu zegara.

Diagram

Diagram stanu dla maszyny Mealy'ego przypisuje wartość wyjściową do każdej krawędzi przejścia, w przeciwieństwie do diagramu stanu dla maszyny Moore'a, który przypisuje wartość wyjściową do każdego stanu.

Gdy zarówno alfabet wejściowy, jak i wyjściowy to $Σ$ , można również powiązać z automatem Mealy'ego graf skierowany helisą ^{[ wymagane wyjaśnienie ]} $(S \times Σ, (x, i) \to (T (x, i), G (x, i)))$ . Ten graf ma jako wierzchołki pary stanów i liter, każdy węzeł jest poza stopniem pierwszym, a następnik $(x, i)$ jest kolejnym stanem automatu i literą, którą automat wypisuje, gdy jest w stanie $x$ i czyta literę $i$ . Ten wykres jest sumą cykli rozłącznych, jeśli automat jest dwuodwracalny ^{[ potrzebna definicja ]} .

Przykłady

Prosty

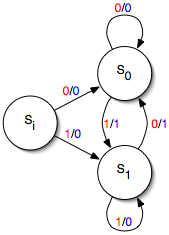
Diagram stanu prostej maszyny Mealy'ego z jednym wejściem i jednym wyjściem. (Dla każdej wartości wejściowej wyprowadzane jest 1, jeśli bieżąca wartość wejściowa różni się od poprzedniej lub 0 w przeciwnym przypadku.)

Prosta maszyna Mealy ma jedno wejście i jedno wyjście. Każda krawędź przejścia jest oznaczona wartością wejścia (pokazaną na czerwono) i wartością wyjścia (pokazaną na niebiesko). Maszyna startuje w stanie $S i$ . (W tym przykładzie wyjściem jest wyłączna lub jedna z dwóch ostatnich wartości wejściowych; w ten sposób maszyna implementuje detektor krawędzi, wysyłając 1 za każdym razem, gdy wejście się zmieni, i 0 w przeciwnym razie).

Złożony

Bardziej złożone maszyny Mealy mogą mieć wiele wejść, jak również wiele wyjść.

Aplikacje

Maszyny Mealy zapewniają podstawowy model matematyczny dla maszyn szyfrujących. Biorąc pod uwagę alfabet wejściowy i wyjściowy alfabet łaciński , można zaprojektować maszynę Mealy, która mając ciąg liter (sekwencję danych wejściowych) może przetworzyć go na zaszyfrowany ciąg (sekwencja danych wyjściowych). Jednakże, chociaż model Mealy'ego mógłby być użyty do opisania Enigmy , diagram stanów byłby zbyt złożony, aby zapewnić wykonalne sposoby projektowania złożonych maszyn szyfrujących.

Maszyny Moore'a/Mealy'ego to DFA , które również generują dane wyjściowe w każdym tyknięciu zegara. Nowoczesne procesory, komputery, telefony komórkowe, zegary cyfrowe i podstawowe urządzenia/maszyny elektroniczne mają do kontrolowania coś w rodzaju skończonej maszyny stanów.

Proste systemy oprogramowania, zwłaszcza te, które można przedstawić za pomocą wyrażeń regularnych , można modelować jako maszyny o skończonych stanach. Takich prostych systemów, jak automaty czy podstawowa elektronika, jest wiele.

Znajdując przecięcie dwóch maszyn skończonych, można w bardzo prosty sposób zaprojektować współbieżne systemy , które na przykład wymieniają komunikaty. Na przykład sygnalizacja świetlna to system składający się z wielu podsystemów, takich jak różne sygnalizacje świetlne, które działają jednocześnie.

Kilka przykładów zastosowań:

klasyfikacja liczbowa
zegarek z timerem
automat do sprzedaży
sygnalizacja świetlna
Skaner kodów kreskowych
pompy gazowe

Zobacz też

przypisy

Mączny, George H. (1955). Metoda syntezy obwodów sekwencyjnych . Dziennik techniczny systemu Bell. s. 1045–1079.
Holcombe, WML (1982). Teoria automatów algebraicznych . Cambridge Studies in Advanced Mathematics. Tom. 1. Cambridge University Press . ISBN 0-521-60492-3 . Zbl 0489.68046 .
Roth, Charles H., Jr. (2004). Podstawy projektowania logiki . Thomson-Engineering. s. 364–367. ISBN 0-534-37804-8 .
Achawi, Ali; Klimann, Ines; Lombardia, Sylvain; Mairesse, Jean; Picantin, Matthieu (2012). „O problemie skończoności dla (pół) grup automatów”. International Journal of Algebra and Computation . 22 (6). ar Xiv : 1105.4725 . Bibcode : 2011arXiv1105.4725A . Zbl 1280.20038 .

Linki zewnętrzne

Media związane z maszyną Mealy w Wikimedia Commons