Metoda wąskiego gardła informacji

Metoda wąskiego gardła informacji to technika w teorii informacji wprowadzona przez Naftalego Tishby'ego , Fernando C. Pereirę i Williama Bialka . Jest przeznaczony do znajdowania najlepszego kompromisu między dokładnością a złożonością ( kompresja ) podczas podsumowywania (np. grupowania ) zmiennej losowej X , biorąc pod uwagę łączny rozkład prawdopodobieństwa p(X,Y) między X a obserwowaną istotną zmienną Y - i sam opisał jako dostarczający „zaskakująco bogatych ram do omawiania różnych problemów związanych z przetwarzaniem i uczeniem się sygnałów” .

Zastosowania obejmują grupowanie dystrybucyjne i redukcję wymiarów , a ostatnio zasugerowano, że jest to teoretyczna podstawa głębokiego uczenia się . Uogólnił klasyczne pojęcie minimalnych wystarczających statystyk ze statystyk parametrycznych na dowolne rozkłady, niekoniecznie wykładnicze. Czyni to poprzez złagodzenie warunku wystarczalności, aby uchwycić pewien ułamek wzajemnej informacji z odpowiednią zmienną Y .

Wąskie gardło informacji można również postrzegać jako problem zniekształcenia szybkości , z funkcją zniekształcenia, która mierzy, jak dobrze prognozuje się Y na podstawie skompresowanej reprezentacji T w porównaniu z jej bezpośrednią prognozą na podstawie X . Ta interpretacja zapewnia ogólny algorytm iteracyjny do rozwiązywania kompromisu związanego z wąskim gardłem informacyjnym i obliczania krzywej informacyjnej z rozkładu p(X,Y) .

Niech skompresowana reprezentacja będzie dana przez zmienną losową ${\ displaystyle T}$ . Algorytm minimalizuje następujący funkcjonał w odniesieniu do rozkładu warunkowego: ${\ displaystyle p (t | x)}$ :

${\ Displaystyle \ min _ {p (t | x)} \, \, ja (X; T) - \ beta ja (T;Y),}$

gdzie ${\ Displaystyle I (X; T)}$ i ${\ Displaystyle I (T; Y)}$ są wzajemnymi informacjami ${\ displaystyle X}$ i $}$${\ displaystyle$$Lagrange'a$ i odpowiednio i $jest$$_$ _ _ _

Teoria informacji głębokiego uczenia się

Teoria wąskich gardeł informacji jest ostatnio wykorzystywana do badania głębokich sieci neuronowych (DNN). Rozważ $warstwę$ wejściową i wyjściową DNN i niech będzie $dowolną$$warstwą$ . Shwartz-Ziv i Tishby zaproponowali $ja$ kompromis między miarami wzajemnej i ${\ Displaystyle I (T, Y)}$ . W $_$ odpowiednio $określają$ _ wejście i wyjście. Przypuszczali, że proces szkolenia DNN składa się z dwóch oddzielnych faz; 1) początkowa faza dopasowania, w której ${\ Displaystyle I (T, Y)}$ wzrasta i 2) kolejna faza kompresji, w której ${\ Displaystyle I (X, T)}$ maleje. Saxe i in. w odparli twierdzenie Shwartz-Ziv i Tishby, stwierdzając, że to zjawisko kompresji w DNN nie jest kompleksowe i zależy od konkretnej funkcji aktywacji. W szczególności twierdzili, że kompresja nie występuje w przypadku funkcji aktywacji ReLu. Shwartz-Ziv i Tishby zakwestionowali te twierdzenia, argumentując, że Saxe i in. nie zaobserwowali kompresji z powodu słabych szacunków wzajemnych informacji. Ostatnio Noshad i in. wykorzystali optymalny estymator wzajemnych informacji do zbadania tej kontrowersji, zauważając, że optymalny estymator oparty na hash ujawnia zjawisko kompresji w szerszym zakresie sieci z aktywacjami ReLu i maxpooling. Z drugiej strony, ostatnio Goldfeld i in. argumentowali, że obserwowana kompresja jest wynikiem zjawisk geometrycznych, a nie zjawisk teorii informacji, pogląd ten podzielano również w .

Wąskie gardło Gaussa

Wąskie gardło Gaussa, czyli zastosowanie podejścia informacyjnego wąskiego gardła do zmiennych Gaussa, prowadzi do rozwiązań związanych z kanoniczną analizą korelacji. Załóżmy, że ${\ Displaystyle X, Y \,}$ są wspólnie wielowymiarowymi zerowymi średnimi wektorami normalnymi z kowariancjami ${\ Displaystyle \ Sigma _ {XX}, \, \, \ Sigma _ {YY}}$ i jest skompresowaną wersją ${\ displaystyle T \,}$$X \,}$ które muszą utrzymywać określoną wartość wzajemnych informacji z ${\ displaystyle Y \,}$ . Można wykazać, że optymalny jest wektorem normalnym składającym się z liniowych kombinacji elementów $gdzie$$\ Displaystyle X, \, \, T = AX \,}$ T ${\ Displaystyle A \,}$ ma ortogonalne rzędy.

Macierz projekcji $}$ rzeczywistości zawiera wiersze wybrane z ważonych lewych wektorów własnych rozkładu macierzy na wartości osobliwe (ogólnie asymetryczne) ${\ displaystyle A \,$

${\ Displaystyle \ Omega = \ Sigma _ {X|Y} \ Sigma _ {XX} ^ {-1} = I- \ Sigma _ {XY} \ Sigma _ {YY} ^ {-1} \ Sigma _ {XY }^{T}\Sigma _{XX}^{-1}.\,}$

Zdefiniuj rozkład na wartości osobliwe

${\ Displaystyle \ Omega = U \ Lambda V ^ {T} {\ tekst {z}} \ Lambda = \ operatorname {Diag} {\big (}\lambda _{1}\leq \lambda _{2}\cdots \lambda _{N}{\big)}\,}$

i wartości krytyczne

${\ Displaystyle \ beta _ {i} ^ {C} {\ underset {\ lambda _ {i}<1} {=}} (1- \ lambda _ {i}) ^ {- 1}. \,}$

wtedy liczba aktywnych wektorów własnych w rzucie lub kolejność aproksymacji jest podana przez ${\ displaystyle M \ ,}$

$\ beta \ równoważnik \ beta _ {M} ^ {C}}$

I w końcu dostajemy

${\ Displaystyle A = [w_ {1} U_ {1}, \ kropki, w_ {M} U_ {M}] ^ {T}}$

W których wagi są podane przez

${\ Displaystyle w_ {i} = {\ sqrt {(\ beta (1- \ lambda _ {i}) / \ lambda _ {i} r_ { I}}}}$

gdzie ${\ Displaystyle r_ {i} = U_ {i} ^ {T} \ Sigma _ {XX} U_ {i}. \,}$

Zastosowanie gaussowskiego wąskiego gardła informacyjnego do szeregów czasowych (procesów) daje rozwiązania związane z optymalnym kodowaniem predykcyjnym. Ta procedura jest formalnie równoważna z liniową analizą cech w zwolnionym tempie.

Optymalne struktury czasowe w liniowych układach dynamicznych można ujawnić w tak zwanym wąskim gardle informacyjnym przeszłości i przyszłości, czyli zastosowaniu metody wąskiego gardła do niegaussowskich próbkowanych danych. Koncepcja, traktowana przez Creutzig, Tishby i in., nie jest pozbawiona komplikacji, ponieważ w ćwiczeniu składają się na nią dwie niezależne fazy: po pierwsze oszacowanie gęstości prawdopodobieństwa nieznanego macierzystego, z którego pobierane są próbki danych, a po drugie wykorzystanie tych gęstości w teoretyczne ramy informacyjne wąskiego gardła.

Oszacowanie gęstości

Główny artykuł: oszacowanie gęstości

$,$ oszacować gęstość prawdopodobieństwa w punktach próbkowania Jest to dobrze znany problem z wieloma rozwiązaniami opisanymi przez Silvermana . W niniejszej metodzie wspólne prawdopodobieństwa próbek są znajdowane przy użyciu macierzy przejść Markowa , co ma pewną matematyczną synergię z samą metodą wąskiego gardła.

Dowolnie rosnąca metryka odległości między wszystkimi parami próbek a macierzą odległości wynosi $jot$ ja , ${i, j} = f {\ duży (}{\Duży |}x_{i}-x_{j}{\Duży |}{\Duży)}}$ . Wtedy prawdopodobieństwa przejść między parami próbek ${\ Displaystyle P_ {i, j} = \ exp (- \ lambda d_ {i, j}) \,}$ dla pewnego ${\ Displaystyle \ lambda > 0 \,}$ musi być obliczone. Traktując próbki jako $znormalizowaną$ wersję jako macierz prawdopodobieństwa przejścia stanu Markowa, wektor prawdopodobieństw „stanów” po $,$ uwarunkowany początkowym stan ${\ Displaystyle p (0) \,}$ jest ${\ Displaystyle p (t) = P ^ {t} p (0) \,}$ . Wektor prawdopodobieństwa równowagi podany w zwykły sposób przez dominujący wektor własny macierzy, który jest niezależny od wektora inicjującego ${\ Displaystyle p (\$$\ ,$${\ displaystyle p (0) \,}$ . Ta metoda przejścia Markowa ustala prawdopodobieństwo w punktach próbkowania, które uważa się za proporcjonalne do tamtejszych gęstości prawdopodobieństw.

Inne interpretacje wykorzystania wartości własnych macierzy odległości $omówione$ w Silverman's Density Estimation for Statistics and Data Analysis .

Klastry

W poniższym przykładzie miękkiego klastrowania wektor odniesienia $próbek$$że wspólne$ zakłada jest znane Klaster miękki $definiowany przez jego rozkład$${\ Displaystyle x_ {i}: \, \, \, p(c_{k}|x_{i})}$ w próbkach danych . Tishby i in. przedstawił następujący iteracyjny zestaw równań do wyznaczania klastrów, które ostatecznie są uogólnieniem algorytmu Blahuta-Arimoto , opracowanego w teorii zniekształceń szybkości . Wydaje się, że zastosowanie tego typu algorytmu w sieciach neuronowych wywodzi się z argumentów dotyczących entropii wynikających z zastosowania rozkładów Gibbsa w wyżarzaniu deterministycznym.

${\ Displaystyle {\ rozpocząć {przypadki} p (c | x) = Kp ( c)\exp {\Duży (}-\beta \,D^{KL}{\Duży [}p(y|x)\,||\,p(y|c){\Duży ]}{\Duży )}\\p(y|c)=\textstyle \sum _{x}p(y|x)p(c|x)p(x){\big /}p(c)\\p(c) =\textstyle \sum _{x}p(c|x)p(x)\\\end{przypadki}}}$

Funkcja każdej linii iteracji rozwija się jako

Linia 1: Jest to zestaw prawdopodobieństw warunkowych o wartościach macierzowych

${\ Displaystyle A_ {i, j} = p (c_ {i} | x_ {j}) = Kp (c_ {i}) \ exp {\ duży (} - \ beta \, D ^ {KL} {\ duży [}p(y|x_{j})\,||\,p(y|c_{i}){\Duży ]}{\Duży )}}$

${KL} \,}$ Kullbacka – Leiblera między wektorami wygenerowanymi przez przykładowe dane a wektorami wygenerowanymi przez zredukowane informacje ${$$Displaystyle D ^$ proxy $jest$ stosowane do oceny wierności skompresowanego wektora w odniesieniu do danych referencyjnych (lub kategorycznych) $z$ równaniem wąskiego gardła. ${\ Displaystyle D ^ {KL} (a||b) \,}$ jest rozbieżnością Kullbacka-Leiblera między rozkładami ${\ Displaystyle a, b \,}$

${\ Displaystyle D ^ {KL} (a || b) = \ suma _ { i}p(a_{i})\log {\Duży (}{\frac {p(a_{i})}{p(b_{i})}}{\Duży)}}$

i $jest$ normalizacją skalarną Ważenie ujemnym wykładnikiem odległości oznacza, że ​​wcześniejsze prawdopodobieństwa skupień są zmniejszane w wierszu 1, gdy dywergencja Kullbacka-Leiblera jest duża, a zatem prawdopodobieństwo pomyślnych skupień wzrasta, podczas gdy nieudane zanikają.

Wiersz 2: Drugi zbiór prawdopodobieństw warunkowych o wartościach macierzowych. Zgodnie z definicją

${\ Displaystyle {\ rozpocząć {wyrównane} p (y_ {i} | c_ {k}) &=\suma _{j}p(y_{i}|x_{j})p(x_{j}|c_{k})\\&=\suma _{j}p(y_{i}|x_ {j})p(x_{j},c_{k}){\big /}p(c_{k})\\&=\suma _{j}p(y_{i}|x_{j}) p(c_{k}|x_{j})p(x_{j}){\big /}p(c_{k})\\\koniec{wyrównane}}}$

gdzie tożsamości Bayesa ${\ Displaystyle p (a, b) = p (a | b) p ( b)=p(b|a)p(a)\,}$ są używane.

Linia 3: ta linia znajduje krańcowy rozkład klastrów do $\ displaystyle c \,}$

${\ Displaystyle {\ rozpocząć {wyrównane} p (c_ {i}) & = \sum _{j}p(c_{i},x_{j})&=\sum _{j}p(c_{i}|x_{j})p(x_{j})\end{wyrównane} }}$

To standardowy wynik.

Dalsze dane wejściowe do algorytmu to krańcowy rozkład próbki, który został już określony przez dominujący wektor własny i $( x )$ rozbieżności Kullbacka – Leiblera o wartości ${\ Displaystyle p (x)$ funkcjonować

$\ Displaystyle D_ {i, j} ^ {KL} = D ^ {KL} {\ Duży [} p (y | x_ {j}) \, ||\, p ( y|c_{i}){\Duży ]}{\Duży )}}$

wyprowadzone z odstępów między próbkami i prawdopodobieństw przejścia.

Macierz ${\ Displaystyle p (y_ {i} | c_ {j}) \,}$ może być inicjowana losowo lub z rozsądnym domysłem, podczas gdy macierz ${\ displaystyle p(c_{i}|x_{j})\,}$ nie wymaga żadnych wcześniejszych wartości. Chociaż algorytm jest zbieżny, może istnieć wiele minimów, które należy rozwiązać.

Definiowanie konturów decyzyjnych

Aby sklasyfikować nową próbkę zewnętrzną $'\,}$ do zbioru treningowego $,$ poprzednia metryka odległości znajduje prawdopodobieństwa przejścia między $displaystyle$ próbki w ${\ Displaystyle X: \, \,}$ , ${\ Displaystyle {\ tylda {p}} (x_ {i}) = p (x_ {i} | x ') = \ operatorname {K} \ exp { \ Duży (} - \ lambda f {\ duży (}{\ Duży |} x_ {i} -x '{\ Duży |} {\ duży)} {\ Duży)}} z K. {\ Displaystyle \$ operatorname $K } \,}$ normalizacja. Po drugie, zastosuj ostatnie dwa wiersze algorytmu 3-wierszowego, aby uzyskać prawdopodobieństwa klastrów i kategorii warunkowych.

${\ Displaystyle {\ rozpocząć {wyrównane} i {\ tylda {p}} (c_ {i}) = p (c_ {i }|x')=\suma _{j}p(c_{i}|x_{j})p(x_{j}|x')=\suma _{j}p(c_{i}|x_{ j}){\tylda {p}}(x_{j})\\&p(y_{i}|c_{j})=\suma _{k}p(y_{i}|x_{k})p (c_{j}|x_{k})p(x_{k}|x')/p(c_{j}|x')=\suma _{k}p(y_{i}|x_{k} )p(c_{j}|x_{k}){\tylda {p}}(x_{k})/{\tylda {p}}(c_{j})\\\koniec{wyrównane}}}$

Wreszcie

${\ Displaystyle p (y_ {i} | x ') = \ suma _ {j} p (y_ {i} | c_ {j}) p (c_ {j} | x')} = \ suma _ {j} p(y_{i}|c_{j}){\tylda {p}}(c_{j})\,}$

Parametr musi być $ściśle$ nadzorowany, ponieważ gdy jest zwiększany od zera, rosnąca liczba cech w przestrzeni prawdopodobieństwa kategorii skupia się na pewnych krytycznych progach

Przykład

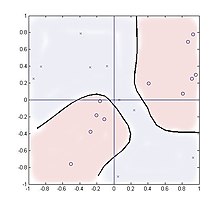
Poniższy przypadek analizuje grupowanie w mnożniku czterokwadrantowym z ${\ Displaystyle y = \ operatorname {znak} (uv) \,}$$wejściami$ kategoriami $,$ generowanymi . Ta funkcja ma dwa przestrzennie oddzielone klastry dla każdej kategorii, co pokazuje, że metoda może obsłużyć takie rozkłady.

Pobiera się 20 próbek, równomiernie rozmieszczonych na kwadracie ${\ Displaystyle [-1,1] ^ {2} \,}$ . Liczba klastrów używanych poza liczbą kategorii, w tym przypadku dwóch, ma niewielki wpływ na wydajność, a wyniki są pokazane dla dwóch klastrów przy użyciu parametrów ${\ Displaystyle \ lambda = 3, \, \ beta =2,5}$ .

Funkcja odległości to ${\ Displaystyle d_ {i, j} = {\ duży |} x_ {i} -x_ {j} {\ duży |} ^ {2}} gdzie x$ ja $Displaystyle x_ {i} = (u_ {i}, v_ {i}) ^ {T} \,}$ podczas gdy rozkład warunkowy ${\ Displaystyle p (y | x) \,}$ to 2 × 20 matryca

${\ Displaystyle {\ rozpocząć {wyrównane} i Pr (y_ {i} = 1) = 1 {\ tekst {jeśli}} \ operatorname {znak} (u_ {i} v_ {i}) = 1 \ \\ i Pr ( y_{i}=-1)=1{\text{if }}\nazwaoperatora {znak} (u_{i}v_{i})=-1\,\end{wyrównane}}}$

i zero gdzie indziej.

Sumowanie w wierszu 2 zawiera tylko dwie wartości reprezentujące wartości treningowe +1 lub -1, ale mimo to działa dobrze. Rysunek przedstawia położenie dwudziestu próbek, przy czym „0” oznacza Y = 1, a „x” oznacza Y = −1. Pokazano kontur na poziomie ilorazu wiarygodności jedności,

${\ Displaystyle L = {\ Frac {\ Pr (1)} {\ Pr (-1)}} = 1}$

$jest$ nowa próbka na kwadracie. Teoretycznie kontur powinien być wyrównany ze $displaystyle v = 0 \,},$$\$ v ale dla tak małych liczb próbek zamiast tego podążali za fałszywymi skupieniami punktów próbkowania.

Kontury decyzyjne

Analogie sieci neuronowych/logiki rozmytej

Algorytm ten jest nieco analogiczny do sieci neuronowej z pojedynczą warstwą ukrytą. Węzły wewnętrzne są reprezentowane przez klastry, $pierwsza$ i druga warstwa wag sieciowych to prawdopodobieństwa warunkowe. $\ Displaystyle p (c_ {j} |x_ {i}) \,}$ i ${\ Displaystyle p (y_ {k} | c_ {j}) \,}$ odpowiednio. Jednak w przeciwieństwie do standardowej sieci neuronowej algorytm opiera się całkowicie na prawdopodobieństwach jako danych wejściowych, a nie na samych wartościach próbek, podczas gdy wartości wewnętrzne i wyjściowe są warunkowymi rozkładami gęstości prawdopodobieństwa. Funkcje nieliniowe są zawarte w metryce odległości $prawdopodobieństwach$ funkcjach wpływających / promieniowych funkcjach bazowych przejścia zamiast funkcji sigmoidalnych.

$\ lambda \,}$ , często w dziesiątkach iteracji, i zmieniając , λ $\ Displaystyle$ i ${\ Displaystyle f \,$ } liczności klastrów, można osiągnąć różne poziomy skupienia się na cechach.

Statystyczna definicja miękkiego klastrowania $pewnym stopniu$ z rozmytej .

Rozszerzenia

Ciekawym rozszerzeniem jest przypadek wąskiego gardła informacyjnego z informacjami pobocznymi. Tutaj maksymalizuje się informacje o jednej zmiennej docelowej i minimalizuje o innej, ucząc się reprezentacji, która zawiera informacje o wybranych aspektach danych. Formalnie

${\ Displaystyle \ min _ {p (t | x)} \, \ ,I(X;T)-\beta ^{+}I(T;Y^{+})+\beta ^{-}I(T;Y^{-})}$

Bibliografia

• Weiss, Y. (1999), „Segmentacja za pomocą wektorów własnych: jednoczący widok”, Proceedings IEEE International Conference on Computer Vision (PDF) , s. 975–982
• P. Harremoës i N. Tishby „Ponowna wizyta w wąskim gardle informacji lub jak wybrać dobrą miarę zniekształceń”. W materiałach Międzynarodowego Sympozjum Teorii Informacji (ISIT) 2007