Modelowanie kombinatoryczne

Modelowanie kombinatoryczne to proces, który pozwala nam zidentyfikować odpowiedni model matematyczny do przeformułowania problemu. Te kombinatoryczne modele zapewnią, poprzez kombinatoryki , operacje potrzebne do rozwiązania problemu.

Niejawne modele kombinatoryczne

Proste problemy kombinatoryczne to takie, które można rozwiązać, stosując tylko jedną operację kombinatoryczną (wariacje, permutacje, kombinacje…). Problemy te można podzielić na trzy różne modele, zwane niejawnymi modelami kombinatorycznymi.

Wybór

Problem selekcji wymaga wybrania próby k elementów ze zbioru n elementów. Trzeba wiedzieć, czy kolejność wybierania obiektów ma znaczenie i czy obiekt można wybrać więcej niż jeden raz, czy nie. Ta tabela pokazuje operacje, które zapewnia model, aby uzyskać liczbę różnych próbek dla każdej selekcji:

	Powtórzenie niedozwolony	Powtórzenie dozwolony
Zamówione próbka	${\ Displaystyle V_ {n, k}}$	${\ Displaystyle VR_ {n, k}}$
Nie zamówione próbka	${\ Displaystyle C_ {n, k}}$	${\ Displaystyle CR_ {n, k}}$

Przykłady

1.- Na imprezie jest 50 osób. Każdy raz każdemu podaje rękę. Jak często podaje się ręce w sumie? To, co musimy zrobić, to obliczyć liczbę wszystkich możliwych par gości przyjęcia, co oznacza próbę 2 osób z 50 gości, więc ${\ displaystyle k = 2}$ i ${\ displaystyle n =50}$ . Para będzie taka sama bez względu na kolejność dwóch osób. Uścisk dłoni musi być wykonany przez dwie różne osoby (bez powtórzeń). Wymagane jest więc wybranie uporządkowanej próbki 2 elementów ze zbioru 50 elementów, w której niedopuszczalne jest powtórzenie. To wszystko, co musimy wiedzieć, aby wybrać odpowiednią operację, a wynikiem jest:

${\ Displaystyle C_ {50,2} = {\ Frac {50!} {2! \ cdot (50-2)!}} = 1225}$

2.- Niestety nie pamiętasz kodu do czterocyfrowego zamka. Wiesz tylko, że nie użyłeś żadnej cyfry więcej niż raz. Ile różnych sposobów musisz wypróbować? Musimy wybrać próbkę 4 cyfr z zestawu 10 cyfr (podstawa 10), więc ${\ displaystyle k = 4}$ i ${\ displaystyle n = 10}$ . Cyfry muszą być uporządkowane w określony sposób, aby uzyskać prawidłowy numer, dlatego chcemy wybrać zamówioną próbkę. Jak mówi oświadczenie, żadna cyfra nie została wybrana więcej niż raz, więc nasza próbka nie będzie miała powtarzających się cyfr. Wymagane jest więc wybranie uporządkowanej próby 4 elementów ze zbioru 10 elementów, w którym niedozwolone są powtórzenia. To wszystko, co musimy wiedzieć, aby wybrać odpowiednią operację, a wynikiem jest:

${\ Displaystyle V_ {10,4} = {\ Frac {10!} {(10-4)!}} = 5040}$

3.- Chłopiec chce kupić 20 zaproszeń dla swoich przyjaciół na przyjęcie urodzinowe. W sklepie są 3 rodzaje kart i wszystkie mu się podobają. Na ile sposobów może kupić 20 kart? Wymagane jest wybranie próbki 20 zaproszeń z zestawu 3 rodzajów kart, więc ${\ displaystyle k = 20}$ i ${\ displaystyle n = 3}$ . Kolejność wyboru różnych rodzajów zaproszeń nie ma znaczenia. Ponieważ rodzaj karty musi być wybrany więcej niż jeden raz, w naszych zaproszeniach pojawią się powtórzenia. Chcemy więc wybrać nieuporządkowaną próbkę 20 elementów ( $)$$powtórzenie$ zbioru 3 elementów ( dozwolone . To wszystko, co musimy wiedzieć, aby wybrać odpowiednią operację, a wynikiem jest:

${\ Displaystyle CR_ {3,20} = C_ {22,20} = {\ Frac {22!} {20! \ cdot (22-20)!}} = 231}$

Dystrybucja

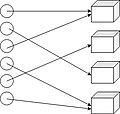
W problemie dystrybucji wymagane jest umieszczenie k obiektów w n skrzynkach lub odbiorcach. Aby wybrać właściwą operację spośród tych, które zapewnia model, należy wiedzieć:

• Czy obiekty są rozróżnialne, czy nie.
• Niezależnie od tego, czy pudełka są rozróżnialne, czy nie.
• Jeśli kolejność, w jakiej przedmioty są umieszczane w pudełku, ma znaczenie.
• Warunki, które musi spełniać dystrybucja. W zależności od tego dystrybucja może być:
  1. Dystrybucja iniekcyjna: każde pudełko musi mieć co najwyżej 1 obiekt ( ${\ displaystyle k \ leq n}$ )
  2. Rozkład suriekcyjny: każde pudełko musi mieć co najmniej 1 obiekt ( ${\ Displaystyle k \ geq n}$ )
  3. Dystrybucja bijektywna: każde pudełko musi mieć dokładnie 1 obiekt ( ${\ displaystyle k = n}$ )
  4. Dystrybucja bez ograniczeń

• 

  Dystrybucja iniekcyjna

• 

  Rozkład surowy

• 

  Dystrybucja bijekcyjna

• 

  Dystrybucja bez ograniczeń

W poniższej tabeli przedstawiono operacje, które zapewnia model, aby uzyskać liczbę różnych sposobów rozmieszczenia obiektów dla każdego z rozkładów:

Rozkład k obiektów na n pudełek

	Dystrybucja nieuporządkowana				Dystrybucja zamówiona
	Rozróżnialne obiekty		Nierozróżnialne przedmioty		Rozróżnialne obiekty
	Wyróżniające się pudełka	Pudełka nie do odróżnienia	Wyróżniające się pudełka	Pudełka nie do odróżnienia	Wyróżniające się pudełka	Pudełka nie do odróżnienia
Każdy dystrybucja	${\ Displaystyle VR_ {n, k}}$	${\ Displaystyle \ suma _ {i = 1} ^ {n} S (k, i)}$	${\ Displaystyle CR_ {n, k}}$	${\ Displaystyle \ suma _ {i = 1} ^ {n} P (k, i)}$	${\ Displaystyle k! \ cdot CR_ {n, k}}$	${\ Displaystyle \ suma _ {i = 1} ^ {n} L (k, i)}$
iniekcyjne dystrybucja	${\ Displaystyle V_ {n, k}}$	${\ Displaystyle 1}$	${\ Displaystyle C_ {n, k}}$	${\ Displaystyle 1}$	${\ Displaystyle V_ {n, k}}$	${\ Displaystyle 1}$
Surjekcja dystrybucja	${\ Displaystyle n! \ cdot S (k, n)}$	${\ Displaystyle S (k, n)}$	${\ Displaystyle CR_ {n, kn}}$	${\ Displaystyle P (k, n)}$	${\ Displaystyle k! \ cdot CR_ {n, kn}}$	${\ Displaystyle L (k, n) = {\ Frac {k!} {n!}} \ cdot {k-1 \ wybierz n-1}}$
Bijektywny dystrybucja	${\ Displaystyle n!}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle n!}$	${\ Displaystyle 1}$

${\ Displaystyle S (k, n) = \ lewo \ {{k \ na szczycie n} \ prawo \}:}$ Liczby Stirlinga drugiego rodzaju

${\ Displaystyle P (k, n):}$ Liczba podziałów liczby całkowitej k na n części

${\ Displaystyle L (k, n):}$ Liczby Lah (liczby Stirlinga trzeciego rodzaju)

Przykłady

1.- Nauczyciel matematyki musi przyznać swoim uczniom 3 stypendia. 7 z nich uzyskało ocenę „wybitną”, więc są kandydatami do ich zdobycia. Na ile sposobów może rozdysponować dotacje? Rozważmy, że 3 stypendia to obiekty, które należy rozmieścić w 7 pudełkach, którymi są studenci. Ponieważ obiekty są identycznymi stypendiami, są nie do odróżnienia. Pudełka można rozróżnić, ponieważ są to różni uczniowie. Każde stypendium musi być przyznane innemu studentowi, więc w każdym pudełku może znajdować się maksymalnie 1 przedmiot. Ponadto kolejność, w jakiej przedmioty są umieszczane w pudełkach, nie ma znaczenia, ponieważ w każdym pudełku nie może być więcej niż jeden przedmiot. $7$ to więc nieuporządkowany rozkład iniekcyjny 3 nierozróżnialnych obiektów ( ) na 7 rozróżnialnych pudełek ( ${\ displaystyle n =$ . To wszystko, co musimy wiedzieć, aby wybrać odpowiednią operację, a wynikiem jest:

${\ Displaystyle C_ {7,3} = {\ Frac {7!} {3! \ cdot (7-3)!}} = 35}$

2.- Grupa 8 przyjaciół wynajmuje 5-pokojowy domek na wakacje. Jeśli pokoje są identyczne i nikt nie może być pusty, na ile sposobów można je rozmieścić w domku? Rozważmy, że przyjaciele to przedmioty, które należy rozmieścić w 5 pudełkach, którymi są pokoje. Ponieważ przedmiotami są różne osoby, można je rozróżnić. Boksy są nie do odróżnienia, ponieważ są to identyczne pomieszczenia. Możemy to uznać za rozkład nieuporządkowany, ponieważ uporządkowanie, w którym wszyscy są umieszczeni w pokojach, nie ma znaczenia. Żaden pokój nie może być pusty, więc w każdym pudełku musi znajdować się co najmniej 1 przedmiot. Jest to więc nieuporządkowany suriekcyjny rozkład 8 rozróżnialnych $)$$)$ 5 . To wszystko, co musimy wiedzieć, aby wybrać odpowiednią operację, a wynikiem jest:

${\ Displaystyle S (8,5) = \ lewo \ {{8 \ na szczycie 5} \ prawo \} = {\ Frac { 1}{5!}}\suma _{i=0}^{5}(-1)^{i}{\binom {5}{i}}(5-i)^{8}=1050}$

3.- 12 osób robi zakupy w supermarkecie, w którym w tej chwili pracuje 4 kasjerów. Na ile różnych sposobów można je rozmieścić w kasach? Rozważmy ludzi jako przedmioty, które należy rozmieścić w pudełkach, które są kasami. Ponieważ ludzie i kasy są różne, przedmioty i pudełka są rozróżnialne. Kolejność umieszczania przedmiotów w pudełkach ma znaczenie, ponieważ są to osoby ustawiające się w kolejkach. W oświadczeniu nie ma mowy o żadnym ograniczeniu. Jest to więc uporządkowany rozkład bez ograniczeń 12 rozróżnialnych obiektów ( $4$ na 4 rozróżnialne pudełka ( ${\ displaystyle n =$ . To wszystko, co musimy wiedzieć, aby wybrać odpowiednią operację, a wynikiem jest:

${\ Displaystyle 12! \ cdot CR_ {4,12} = 12! \ cdot C_ {15,12} = 12! \ cdot {\ Frac {15!} {12! \ cdot (15-12)!} }=217945728000}$

Przegroda

Problem podziału wymaga podzielenia zbioru k elementów na n podzbiorów. Ten model jest powiązany z modelem dystrybucyjnym, ponieważ możemy traktować obiekty w każdym pudełku jako podzbiory zbioru obiektów do dystrybucji. Tak więc każdy z 24 opisanych wcześniej rozkładów ma pasujący rodzaj podziału na podzbiory. Tak więc problem partycji można rozwiązać, przekształcając go w dystrybucję i stosując odpowiednią operację dostarczoną przez model dystrybucji (poprzednia tabela). Postępując zgodnie z tą metodą, otrzymamy liczbę możliwych sposobów podziału zbioru. Relacja między tymi dwoma modelami została opisana w poniższej tabeli:

Dystrybucja	Przegroda
Zamówione	Podzbiory uporządkowanych elementów
Nie zamówione	Podzbiory elementów nieuporządkowanych
Rozróżnialne obiekty	Elementy wyróżniające
Nierozróżnialne przedmioty	Nierozróżnialne elementy
Wyróżniające się pudełka	Zamówione partycje
Pudełka nie do odróżnienia	Nieuporządkowane partycje
Dystrybucja iniekcyjna	Podzbiory 1 elementu lub puste
Dystrybucja suriektywna	Brak pustych podzbiorów
Dystrybucja bijekcyjna	Podzbiory dokładnie 1 elementu
Bez ograniczeń	Podzbiory 1 lub więcej elementów lub puste

Relacja ta pozwoliła nam przekształcić tablicę dostarczoną przez model rozkładu w nową, za pomocą której można poznać różne sposoby dzielenia zbioru k elementów na n podzbiorów:

Podział zbioru k elementów na n podzbiorów

	Elementy nieuporządkowane				,
	Elementy wyróżniające		Nierozróżnialne elementy		Elementy wyróżniające
	Uporządkowane podzbiory	Nieuporządkowane podzbiory	Uporządkowane podzbiory	Nieuporządkowane podzbiory	Uporządkowane podzbiory	Nieuporządkowane podzbiory
Dowolne podzbiory	${\ Displaystyle VR_ {n, k}}$	${\ Displaystyle \ suma _ {i = 1} ^ {n} S (k, i)}$	${\ Displaystyle CR_ {n, k}}$	${\ Displaystyle \ suma _ {i = 1} ^ {n} P (k, i)}$	${\ Displaystyle k! \ cdot CR_ {n, k}}$	${\ Displaystyle \ suma _ {i = 1} ^ {n} L (k, i)}$
Puste lub 1-elementowe podzbiory	${\ Displaystyle V_ {n, k}}$	${\ Displaystyle 1}$	${\ Displaystyle C_ {n, k}}$	${\ Displaystyle 1}$	${\ Displaystyle V_ {n, k}}$	${\ Displaystyle 1}$
Brak pustych podzbiorów	${\ Displaystyle n! \ cdot S (k, n)}$	${\ Displaystyle S (k, n)}$	${\ Displaystyle CR_ {n, kn}}$	${\ Displaystyle P (k, n)}$	${\ Displaystyle k! \ cdot CR_ {n, kn}}$	${\ Displaystyle L (k, n) = {\ Frac {k!} {n!}} \ cdot CR_ {n, kn}}$
Podzbiory 1 elementu	${\ Displaystyle n!}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle 1}$	${\ Displaystyle n!}$	${\ Displaystyle 1}$

Przykłady

1.- Grupa 3 kolegów z klasy musi napisać pracę dyplomową na 8 różnych tematów z matematyki. Na ile sposobów mogą podzielić pracę do wykonania? Musimy podzielić zestaw 8 tematów na 3 podzbiory. Te podzbiory będą tematami, nad którymi każdy z uczniów będzie pracował. Elementy w zbiorze (tematy) są rozróżnialne. Partycje muszą być uporządkowane, ponieważ każda z nich będzie odpowiadać innemu studentowi, ale tematy w każdym podzbiorze nie muszą być uporządkowane, ponieważ każdy student może zdecydować, w jakiej kolejności postępować podczas pracy nad pracą dyplomową. Oświadczenie nie wspomina o żadnym ograniczeniu podzbiorów. $elementów$ podzielenie zbioru 8 elementów ( $)$ 3 uporządkowane . To wszystko, co musimy wiedzieć, aby wybrać odpowiednią operację, a wynikiem jest:

${\ Displaystyle VR_ {3,8} = 3 ^ {8} = 6561}$

Zobacz też

• Dwunasty sposób

Źródła

• Dubois, Jean-Guy. Une systématique des configurations combinatoires simples. Studia pedagogiczne z matematyki 15 , 37–57 (1984) doi:10.1007/BF00380438
• V. Navarro-Pelayo; Carmen Batanero ; Juan D. Godino (1996). Razonamiento Combinatorio en Alumnos de Secundaria.
• Rafael Roa (2000). Razonamiento Combinatorio en Estudiantes con Preparación Matemática Avanzada.
• Tan Mingshu (2011). Niektóre kombinatoryczne tożsamości i wyjaśnienia oparte na modelu zajętości.