Moment pędu światła

Całkowity moment pędu światła składa się z dwóch składowych, z których obie działają w inny sposób na masywną cząstkę koloidalną wprowadzoną do wiązki. Składowa spinowa powoduje, że cząstka obraca się wokół własnej osi, podczas gdy druga składowa, znana jako orbitalny moment pędu (OAM), powoduje obrót cząstki wokół osi wiązki.

Moment pędu światła jest wielkością wektorową wyrażającą wielkość dynamicznej rotacji występującej w polu elektromagnetycznym światła . Poruszając się w przybliżeniu po linii prostej, wiązka światła może też obracać się (lub " kręcić " lub " skręcać " ) wokół własnej osi. Rotacja ta, choć niewidoczna gołym okiem , może zostać ujawniona poprzez oddziaływanie wiązki światła z materią.

Istnieją dwie różne formy rotacji wiązki światła, jedna związana z jej polaryzacją , a druga z kształtem czoła fali . Te dwie formy rotacji są zatem powiązane z dwiema różnymi postaciami momentu pędu , odpowiednio nazwanymi lekkim spinowym momentem pędu (SAM) i lekkim orbitalnym momentem pędu (OAM).

Całkowity moment pędu światła (lub, bardziej ogólnie, pola elektromagnetycznego i innych pól sił ) i materii jest zachowany w czasie.

Wstęp

Światło, a ogólniej fala elektromagnetyczna niesie ze sobą nie tylko energię , ale także pęd , który jest cechą charakterystyczną wszystkich obiektów w ruchu postępowym . Istnienie tego pędu uwidacznia się w zjawisku „ ciśnienia promieniowania ” , w którym wiązka światła przekazuje swój pęd obiektowi pochłaniającemu lub rozpraszającemu, wytwarzając w tym procesie nacisk mechaniczny.

Światło może również przenosić moment pędu , który jest własnością wszystkich obiektów w ruchu obrotowym. Na przykład wiązka światła może obracać się wokół własnej osi podczas propagacji do przodu. Ponownie, istnienie tego momentu pędu można wykazać, przenosząc go na małe absorbujące lub rozpraszające cząstki, które w ten sposób podlegają optycznemu momentowi obrotowemu.

W przypadku wiązki światła można zazwyczaj wyróżnić dwie „ formy rotacji ” , pierwszą związaną z dynamicznym obrotem pól elektrycznych i magnetycznych wokół kierunku propagacji, a drugą z dynamicznym obrotem promieni świetlnych wokół głównej osi wiązki. Te dwa obroty są związane z dwiema formami momentu pędu , a mianowicie SAM i OAM. Jednak rozróżnienie to zaciera się w przypadku silnie skupionych lub rozbieżnych wiązek, aw ogólnym przypadku można zdefiniować tylko całkowity moment pędu pola świetlnego. Ważnym przypadkiem granicznym, w którym rozróżnienie jest zamiast tego jasne i jednoznaczne, jest „ przyosiowa ” wiązka światła, to znaczy dobrze skolimowana wiązka, w której wszystkie promienie świetlne (a dokładniej wszystkie składowe Fouriera pola optycznego ) tylko tworzą małe kąty z osią wiązki .

Dla takiej wiązki SAM jest ściśle powiązany z polaryzacją optyczną , aw szczególności z tzw. polaryzacją kołową . OAM jest związany z przestrzennym rozkładem pola, aw szczególności z czoła fali .

Oprócz tych dwóch wyrazów, jeśli początek współrzędnych znajduje się poza osią belki, występuje trzeci udział momentu pędu uzyskany jako iloczyn poprzeczny położenia belki i jej całkowitego pędu . Ten trzeci termin jest również nazywany „ orbitalnym ” , ponieważ zależy od przestrzennego rozkładu pola. Jednakże, ponieważ jego wartość zależy od wyboru pochodzenia, jest określany jako „ zewnętrzny ” orbitalny moment pędu , w przeciwieństwie do „ wewnętrznego ” OAM występującego dla wiązek spiralnych.

Wyrażenia matematyczne na moment pędu światła

Jednym z powszechnie używanych wyrażeń na całkowity moment pędu pola elektromagnetycznego jest następujące, w którym nie ma wyraźnego rozróżnienia między dwiema formami rotacji:

$${\ Displaystyle \ mathbf {J} = \ varepsilon _ {0} \ int \ mathbf {r} \ razy \ lewo (\ mathbf {E} \ razy \ mathbf {B} \right)d^{3}\mathbf {r} ,}$$

gdzie ${$ są odpowiednio polami $E} }$ i magnetycznymi, to przenikalność próżni i używamy mi ${\ displaystyle \$ Jednostki SI.

Jednak innym wyrazem momentu pędu naturalnie wynikającym z twierdzenia Noether jest następujący, w którym istnieją dwa oddzielne terminy, które można powiązać z SAM ( $)$ i OAM ( $\mathbf {L} }$${\$ ):

$${\ Displaystyle \ mathbf {J} =\varepsilon _{0}\int \left(\mathbf {E} \times \mathbf {A} \right)d^{3}\mathbf {r} +\varepsilon _{0}\sum _{i= x,y,z}\int \left(E^{i}\left(\mathbf {r} \times {\boldsymbol {\nabla }}\right)A^{i}\right)d^{3} \mathbf {r} =\mathbf {S} +\mathbf {L} ,}$$

gdzie jest potencjałem wektorowym $magnetycznego$ , a i - symbole z indeksem górnym oznaczają składowe kartezjańskie odpowiednich wektorów.

Można udowodnić, że te dwa wyrażenia są sobie równoważne dla dowolnego pola elektromagnetycznego, które zanika wystarczająco szybko poza skończonym obszarem przestrzeni. Jednak dwa terminy w drugim wyrażeniu są fizycznie niejednoznaczne, ponieważ nie są niezmienne z cechowaniem . Wersję niezmienną z cechowania można uzyskać, zastępując potencjał wektorowy A i pole elektryczne E ich składową „poprzeczną” lub radiacyjną ${\ Displaystyle \ mathbf {A} _ {\ perp}}$ i ${\ Displaystyle \ \ mathbf {E} _{\perp }}$ , uzyskując w ten sposób następujące wyrażenie:

$${\ Displaystyle \ mathbf {J} _ {\ sprawca} = \ varepsilon _ {0} \ int \ lewo (\ mathbf {E} _ {\ sprawca} \ razy \ mathbf {A} _ {\ sprawca} \ po prawej) d^{3}\mathbf {r} +\varepsilon _{0}\sum _{i=x,y}\int \left({E^{i}}_{\perp}\left(\mathbf { r} \times {\boldsymbol {\nabla}}\right)A_{\sprawa}^{i}\right)d^{3}\mathbf {r} .}$$

Nie podano jeszcze uzasadnienia dla podjęcia tego kroku. To ostatnie wyrażenie ma dalsze problemy, ponieważ można wykazać, że te dwa wyrażenia nie są prawdziwymi momentami pędu, ponieważ nie są zgodne z prawidłowymi regułami komutacji kwantowej. Zamiast tego ich suma, czyli całkowity moment pędu.

Równoważne, ale prostsze wyrażenie dla fali monochromatycznej o częstotliwości ω, wykorzystujące zespoloną notację pól, jest następujące:

$${\ Displaystyle \ mathbf {J} = {\ Frac {\ varepsilon _ {0}} {2i \ omega}} \ int \ lewo (\ mathbf {E} ^ {\ ast} \ razy \ mathbf {E} \ dobrze )d^{3}\mathbf {r} +{\frac {\varepsilon _{0}}{2i\omega }}\sum _{i=x,y,z}\int \left({E^{ i}}^{\ast}\left(\mathbf {r} \times {\boldsymbol {\nabla}}\right)E^{i}\right)d^{3}\mathbf {r} .}$$

Rozważmy teraz granicę przyosiową, przy założeniu, że oś belki pokrywa się z osią z układu współrzędnych. W tej granicy jedyną istotną składową momentu pędu jest jedynka z, czyli moment pędu mierzący obrót wiązki światła wokół własnej osi, podczas gdy pozostałe dwie składowe są pomijalne.

$${\ Displaystyle \ mathbf {J} \ około {\ Frac {{\ kapelusz {z}} \ epsilon _ {0}} {2 \ omega}} \ int \ lewo (\ lewo | E_ {\ tekst {L}} \right|^{2}-\left|E_{\text{R}}\right|^{2}\right)d^{3}\mathbf {r} +{\frac {{\hat {z} }\varepsilon _{0}}{2i\omega }}\int \sum _{i=x,y,z}\left({E^{i}}^{\ast}{\frac {\częściowy} {\częściowe \phi}}E^{i}\right)d^{3}\mathbf {r} .}$$

gdzie $i$$.$ lewą i prawą kołowej

Wymiana spinu i orbitalnego momentu pędu z materią

Oddziaływanie spinu i orbitalnego momentu pędu z materią

Kiedy wiązka światła o niezerowym momencie pędu uderza w cząstkę pochłaniającą, jej moment pędu może zostać przeniesiony na cząstkę, wprawiając ją w ten sposób w ruch obrotowy. Dzieje się tak zarówno w przypadku SAM, jak i OAM. Jeśli jednak cząstka nie znajduje się w środku wiązki, dwa momenty pędu spowodują różne rodzaje rotacji cząstki. SAM spowoduje obrót cząstki wokół własnego środka, tj. wirowanie cząstki. Zamiast tego OAM wygeneruje obrót cząstki wokół osi wiązki. Zjawiska te są schematycznie zilustrowane na rysunku.

W przypadku ośrodków przezroczystych, w granicy przyosiowej, optyczny SAM jest wymieniany głównie z układami anizotropowymi, na przykład kryształami dwójłomnymi . Rzeczywiście, cienkie płytki dwójłomnych kryształów są powszechnie używane do manipulowania polaryzacją światła. Ilekroć zmienia się eliptyczność polaryzacji, w procesie następuje wymiana SAM między światłem a kryształem. Jeśli kryształ może się swobodnie obracać, zrobi to. W przeciwnym razie SAM zostanie ostatecznie przeniesiony do posiadacza i na Ziemię.

Spiralna płyta fazowa (SPP)

Schemat generowania lekkiego orbitalnego momentu pędu za pomocą spiralnej płytki fazowej.

W granicy przyosiowej OAM wiązki światła może być wymieniany z ośrodkami materialnymi, które mają poprzeczną niejednorodność przestrzenną. Na przykład wiązka światła może uzyskać OAM, przechodząc przez spiralną płytkę fazową o niejednorodnej grubości (patrz rysunek).

Hologram Pitch-Fork

Schemat przedstawiający generowanie orbitalnego momentu pędu światła w wiązce Gaussa.

Bardziej wygodne podejście do generowania OAM opiera się na wykorzystaniu dyfrakcji na hologramie przypominającym widelec lub widły (patrz rysunek). Hologramy można również generować dynamicznie pod kontrolą komputera za pomocą przestrzennego modulatora światła .

Płyta Q

Efekt płytki q dla polaryzacji kołowej lewej i prawej strony.

Inna metoda generowania OAM opiera się na sprzężeniu SAM-OAM, które może zachodzić w ośrodku, który jest zarówno anizotropowy, jak i niejednorodny. W szczególności tak zwana płytka q to urządzenie, obecnie realizowane przy użyciu ciekłych kryształów, polimerów lub siatek podfalowych, które może generować OAM poprzez wykorzystanie zmiany znaku SAM. W tym przypadku znak OAM jest kontrolowany przez polaryzację wejściową.

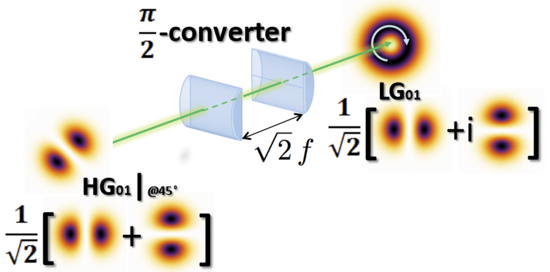
Cylindryczne konwertery trybów

pi/2-cylindryczny konwerter trybów przekształca tryb HG we właściwy tryb LG.

OAM można również wygenerować, przekształcając wiązkę Hermite-Gaussa w wiązkę Laguerre-Gaussa przy użyciu systemu astygmatycznego z dwiema dobrze ustawionymi cylindrycznymi soczewkami umieszczonymi w określonej odległości (patrz rysunek) w celu wprowadzenia dobrze określonej fazy względnej między belki poziome i pionowe Hermite-Gaussa.

Możliwe zastosowania orbitalnego momentu pędu światła

Zastosowania spinowego momentu pędu światła są nie do odróżnienia od niezliczonych zastosowań polaryzacji światła i nie będą tutaj omawiane. Zamiast tego obecnie przedmiotem badań są możliwe zastosowania orbitalnego momentu pędu światła. W szczególności następujące zastosowania zostały już zademonstrowane w laboratoriach badawczych, choć nie osiągnęły jeszcze etapu komercjalizacji:

1. Orientacyjna manipulacja cząstkami lub agregatami cząstek w pęsecie optycznej
2. Kodowanie informacji o dużej przepustowości w komunikacji optycznej w wolnej przestrzeni
3. Wysokowymiarowe kodowanie informacji kwantowych na potrzeby przyszłych zastosowań kryptografii kwantowej lub obliczeń kwantowych
4. Czuła detekcja optyczna

Zobacz też

• Moment pędu
• Polaryzacja kołowa
• Fala elektromagnetyczna
• Równanie Helmholtza
• Światło
• Lekki orbitalny moment pędu
• Lekki spinowy moment pędu
• Wiry optyczne
• Orbitalne multipleksowanie momentu pędu
• Polaryzacja (fale)
• Polaryzacja fotonów

Linki zewnętrzne

• Forbitach
• Glasgow Optyka Grupa
• Instytut Fizyki w Leiden
• ICFO
• Università Di Napoli „Federico II” zarchiwizowane 2016-03-04 w Wayback Machine
• Università Di Roma „La Sapienza”
• Uniwersytet w Ottawie

Dalsza lektura

•   Allen, L.; Barnett, Stephen M. & Padgett, Miles J. (2003). Optyczny moment pędu . Bristol: Instytut Fizyki. ISBN 978-0-7503-0901-1 .
•   Torres, Juan P. & Torner, Lluis (2011). Skręcone fotony: zastosowania światła z orbitalnym momentem pędu . Bristol: Wiley-VCH. ISBN 978-3-527-40907-5 .
•   Andrews, David L. & Babiker, Mohamed (2012). Moment pędu światła . Cambridge: Cambridge University Press. P. 448. ISBN 978-1-107-00634-8 .