Nieukorzenione drzewo binarne

Kladogram w postaci nieukorzenionego drzewa binarnego, przedstawiający podobieństwa i historię ewolucji między gatunkami promieniowców .

W matematyce i informatyce nieukorzenione drzewo binarne to nieukorzenione drzewo , w którym każdy wierzchołek ma jednego lub trzech sąsiadów.

Definicje

Drzewo wolne lub drzewo nieukorzenione to spójny graf nieskierowany bez cykli . Wierzchołki z jednym sąsiadem to liście drzewa, a pozostałe wierzchołki to wewnętrzne węzły drzewa. Stopień wierzchołka to liczba jego sąsiadów; w drzewie z więcej niż jednym węzłem liście są wierzchołkami pierwszego stopnia. Nieukorzenione drzewo binarne to drzewo wolne, w którym wszystkie wewnętrzne węzły mają stopień dokładnie trzeci.

W niektórych zastosowaniach sensowne może być rozróżnienie podtypów nieukorzenionych drzew binarnych: płaskie osadzenie drzewa można ustalić, określając cykliczne uporządkowanie krawędzi w każdym wierzchołku, tworząc drzewo płaskie . W informatyce drzewa binarne są często zakorzenione i uporządkowane, gdy są używane jako struktury danych , ale w zastosowaniach nieukorzenionych drzew binarnych w hierarchicznym grupowaniu i rekonstrukcji drzew ewolucyjnych drzewa nieuporządkowane są bardziej powszechne.

Dodatkowo można rozróżnić drzewa, w których wszystkie wierzchołki mają odrębne etykiety, drzewa, w których tylko liście są oznaczone, oraz drzewa, w których węzły nie są oznaczone. W nieukorzenionym drzewie binarnym o n liściach będzie n − 2 węzłów wewnętrznych, więc etykiety mogą być wzięte ze zbioru liczb całkowitych od 1 do 2 n − 1, gdy mają być oznakowane wszystkie węzły, lub ze zbioru liczb całkowitych od 1 do n , gdy etykietowane mają być tylko liście.

Powiązane struktury

Ukorzenione drzewa binarne

Główny artykuł: Zakorzenione drzewo binarne

Nieukorzenione drzewo binarne T można przekształcić w w pełni ukorzenione drzewo binarne (to znaczy ukorzenione drzewo, w którym każdy węzeł niebędący liściem ma dokładnie dwoje dzieci), wybierając krawędź korzenia e z T , umieszczając nowy węzeł główny w środku z e i skierowanie każdej krawędzi wynikowego podzielonego drzewa z dala od węzła głównego. I odwrotnie, każde w pełni zakorzenione drzewo binarne można przekształcić w nieukorzenione drzewo binarne, usuwając węzeł główny, zastępując ścieżkę między jego dwojgiem dzieci pojedynczą niekierowaną krawędzią i tłumiąc orientację pozostałych krawędzi na grafie. Z tego powodu jest dokładnie 2 n −3 razy więcej w pełni ukorzenionych drzew binarnych o n liściach niż nieukorzenionych drzew binarnych o n liściach.

Grupowanie hierarchiczne

Hierarchiczne grupowanie zbioru obiektów można sformalizować jako maksymalną rodzinę zbiorów obiektów, w której nie krzyżują się żadne dwa zbiory. Oznacza to, że dla każdych dwóch zestawów S i T w rodzinie albo S i T są rozłączne, albo jeden jest podzbiorem drugiego, i nie można dodać więcej zestawów do rodziny, zachowując tę ​​​​właściwość. Jeśli T jest nieukorzenionym drzewem binarnym, definiuje hierarchiczne grupowanie swoich liści: dla każdej krawędzi ( u , v ) w T istnieje klaster składający się z liści, które są bliżej u niż v i te zbiory wraz ze zbiorem pustym i zbiorem wszystkich liści tworzą maksymalnie nieprzecinającą się rodzinę. I odwrotnie, z dowolnej maksymalnej nie krzyżującej się rodziny zbiorów na zbiorze n elementów można utworzyć unikalne nieukorzenione drzewo binarne, które ma węzeł dla każdej trójki ( A , B , C ) rozłącznych zbiorów w rodzinie, które razem obejmują wszystkie elementów.

Drzewa ewolucyjne

Zgodnie z prostymi formami teorii ewolucji , historię życia można podsumować jako drzewo filogenetyczne , w którym każdy węzeł opisuje gatunek, liście reprezentują gatunki, które istnieją dzisiaj, a krawędzie reprezentują relacje przodek-potomek między gatunkami. To drzewo ma naturalną orientację od przodków do potomków i korzeń u wspólnego przodka gatunku, więc jest to drzewo ukorzenione. Jednak niektóre metody rekonstrukcji drzew binarnych umożliwiają rekonstrukcję tylko węzłów i krawędzi tego drzewa, ale nie ich orientacji.

Na przykład metody kladystyczne , takie jak maksymalna oszczędność użyć jako danych zestawu binarnych atrybutów opisujących cechy gatunku. Metody te poszukują drzewa z danym gatunkiem jako liśćmi, w których wewnętrzne węzły są również oznaczone cechami, i próbują zminimalizować liczbę przypadków, w których jakaś cecha jest obecna tylko w jednym z dwóch punktów końcowych krawędzi drzewa. Idealnie, każda cecha powinna mieć tylko jedną krawędź, dla której tak jest. Zmiana korzenia drzewa nie zmienia tej liczby różnic krawędzi, więc metody oparte na oszczędności nie są w stanie określić położenia korzenia drzewa i utworzą nieukorzenione drzewo, często nieukorzenione drzewo binarne.

Nieukorzenione drzewa binarne są również tworzone za pomocą metod wnioskowania o drzewach ewolucyjnych na podstawie danych kwartetowych określających, dla każdych czterech gatunków liści, nieukorzenione drzewo binarne opisujące ewolucję tych czterech gatunków, oraz za pomocą metod wykorzystujących odległość kwartetową do pomiaru odległości między drzewami .

Rozkład gałęzi

Nieukorzenione drzewa binarne są również używane do definiowania rozgałęzień grafów poprzez utworzenie nieukorzenionego drzewa binarnego, którego liście reprezentują krawędzie danego grafu. Oznacza to, że rozkład gałęzi można postrzegać jako hierarchiczne grupowanie krawędzi grafu. Rozkłady gałęzi i związana z nimi wielkość liczbowa, szerokość gałęzi, są ściśle związane z szerokością drzewa i stanowią podstawę wydajnych algorytmów programowania dynamicznego na grafach.

Wyliczenie

Ze względu na ich zastosowanie w hierarchicznym klastrowaniu, najbardziej naturalnym problemem wyliczania grafów na nieukorzenionych drzewach binarnych jest policzenie liczby drzew z n oznaczonymi liśćmi i nieoznakowanymi węzłami wewnętrznymi. Nieukorzenione drzewo binarne na n oznakowanych liściach można utworzyć, łącząc n -ty liść z nowym węzłem pośrodku dowolnej krawędzi nieukorzenionego drzewa binarnego na n - 1 oznakowanych liściach. Istnieje 2 n − 5 krawędzi, do których można dołączyć n- ty węzeł; zatem liczba drzew na n liści jest większa niż liczba drzew na n - 1 liściach o współczynnik 2 n - 5. Zatem liczba drzew na n oznaczonych liściach jest podwójną silnią

${\ Displaystyle (2n-5) !! = {\ Frac {(2n-4)!} {(n-2)! 2 ^ {n-2}}}.}$

Numery drzew na 2, 3, 4, 5, ... oznaczonych liściach to

1, 1, 3, 15, 105, 945, 10395, 135135, 2027025, 34459425, ... (sekwencja A001147 w OEIS ).

Podstawowe równości

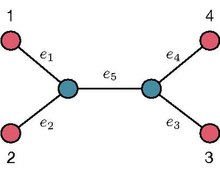
Długość ścieżki od liścia do liścia na ustalonym niezrootowanym drzewie binarnym (UBT) T koduje liczbę krawędzi należących do unikalnej ścieżki w T łączącej dany liść z innym liściem. Na przykład, odnosząc się do UBT $między$ długość ścieżki liśćmi 1 i 2 jest równa 2, podczas gdy długość ścieżki ${\ Displaystyle p_ {1,3}}$ między liśćmi 1 i 3 jest równe 3. Sekwencja długości ścieżki z danego liścia na ustalonym UBT T koduje długości ścieżek z danego liścia do wszystkich pozostałe. Na przykład, odnosząc się do UBT pokazanego na obrazku po prawej stronie, sekwencja długości ścieżki z liścia 1 to ${\ Displaystyle p_ {1} = (p_ {1,2}, p_ {1,3}, p_{1,4})=(2,3,3)}$ . Zbiór sekwencji o długości ścieżki związany z liśćmi T jest zwykle określany jako zbiór sekwencji o długości ścieżki z T .

Przykład nieukorzenionego drzewa binarnego z czterema liśćmi

Daniele Catanzaro, Raffaele Pesenti i Laurence Wolsey wykazali, że zbiór sekwencji długości ścieżki kodujący dany UBT z n liśćmi musi spełniać określone równości, a mianowicie

• ${\ Displaystyle p_ {i, i} = 0}$ dla wszystkich ${\ Displaystyle i \ w [1, n]}$
• ${\ Displaystyle p_ {i, j} = p_ {j, i}}$ dla wszystkich ${\ Displaystyle i, j \ w [ 1,n]:i\neq j}$
• ${\ Displaystyle p_ {i, i} \ równoważnik p_ {i, k} + p_ {k, j}}$ dla wszystkich ${\ Displaystyle i, j, k \ w [1, n]: i \ neq j \ neq k}$
• ${\ Displaystyle \ suma _ {j = 1} ^ {n} 1/2 ^ {p_ {i, j}} = 1/2}$ dla wszystkich ${\ Displaystyle i \ w [1, n]}$ (co jest adaptacją nierówności Krafta-McMillana )
• ${\ Displaystyle \ suma _ {i = 1} ^ {n} \ suma _ {j = 1} ^ { n}p_{i,j}/2^{p_{i,j}}=2n-3}$ , określane również jako rozmaitość filogenetyczna .

Udowodniono, że te równości są konieczne i niezależne dla zbioru długości ścieżki do zakodowania UBT z n liśćmi. Obecnie nie wiadomo, czy są one również wystarczające.

Alternatywne nazwy

Nieukorzenione drzewa binarne były również nazywane wolnymi drzewami binarnymi , drzewami sześciennymi , drzewami trójskładnikowymi i nieukorzenionymi drzewami trójskładnikowymi . Jednak nazwa „wolne drzewo binarne” była również stosowana do drzew nieukorzenionych, które mogą mieć węzły drugiego stopnia, oraz do zakorzenionych drzew binarnych z nieuporządkowanymi dziećmi, a nazwa „drzewo trójskładnikowe” jest częściej używana w odniesieniu do drzewa ukorzenionego z trzema dzieci na węzeł .

Notatki

•   Łysiejący, DJ; Biskup Marcin J.; Cannings, Christopher (2007), Podręcznik genetyki statystycznej , tom. 1 (wyd. 3), Wiley-Interscience, s. 502, ISBN 978-0-470-05830-5 .
• Cilibrasi, Rudi; Vitanyi, Paul MB (2006). „Nowa heurystyka drzewa kwartetowego dla hierarchicznego grupowania”. arXiv : cs/0606048 . .
• Czumaj, Artur; Gibbons, Alan (1996), „Problem Guthriego: nowe równoważności i szybkie redukcje”, Theoretical Computer Science , 154 (1): 3–22, doi : 10.1016/0304-3975 (95) 00126-3 .
•   Eppstein, David (2009), „Squarepants in a tree: Sum of subtree clustering and hyperbolic pants decomposition”, ACM Transactions on Algorithms , 5 (3): 1–24, arXiv : cs.CG/0604034 , doi : 10.1145/1541885.1541890 , S2CID 2434 .
• Exoo, Geoffrey (1996), „Prosta metoda konstruowania małych wykresów sześciennych obwodów 14, 15 i 16” (PDF) , Electronic Journal of Combinatorics , 3 (1): R30, doi : 10,37236/1254 .
•   Furnas, George W. (1984), „Generowanie losowych, binarnych drzew nieuporządkowanych”, Journal of Classification , 1 (1): 187–233, doi : 10.1007 / BF01890123 , S2CID 121121529 .
• Harary, Frank ; Palmer, EM; Robinson, RW (1992), „Zliczanie wolnych drzew binarnych przyjmujących określoną wysokość” (PDF) , Journal of Combinatorics, Information and System Sciences , 17 : 175–181 .
•   Hendy, Michael D.; Penny, David (1989), „Rama ilościowego badania drzew ewolucyjnych”, Systematic Biology , 38 (4): 297–309, doi : 10.2307/2992396 , JSTOR 2992396
• Przytycka, Teresa M .; Larmore, Lawrence L. (1994), „Powrót do problemu optymalnego drzewa alfabetycznego”, Proc. 21. Międzynarodowe Kolokwium Automatów, Języków i Programowania (ICALP '94) , Notatki z wykładów z informatyki, tom. 820, Springer-Verlag, s. 251–262, doi : 10.1007/3-540-58201-0_73 .
• Robertson, Neil ; Seymour, Paul D. (1991), „Graph minors. X. Przeszkody w rozkładzie drzewa”, Journal of Combinatorial Theory , 52 (2): 153–190, doi : 10.1016/0095-8956 (91) 90061-N .
•   św. Jana, Katarzyny; Warnow, Tandy ; Moret, Bernard ME ; Vawterd, Lisa (2003), „Badanie wydajności metod filogenetycznych: (nieważone) metody kwartetowe i łączenie sąsiadów” (PDF) , Journal of Algorithms , 48 (1): 173–193, doi : 10.1016 / S0196-6774 (03 )00049-X , S2CID 5550338 .