Obliczanie cyklicznych kontroli redundancji

Obliczenie cyklicznej kontroli redundancji wywodzi się z matematyki dzielenia wielomianowego modulo dwa . W praktyce przypomina to długie dzielenie łańcucha komunikatu binarnego , z dołączoną stałą liczbą zer, przez ciąg „wielomianu generatora”, z wyjątkiem tego, że operacje wykluczające lub operacje zastępują odejmowanie. Podział tego typu jest skutecznie realizowany w sprzęcie za pomocą zmodyfikowanego rejestru przesuwnego , aw oprogramowaniu za pomocą szeregu równoważnych algorytmów , zaczynając od prostego kodu zbliżonego do matematyki i stając się szybszym (i prawdopodobnie bardziej zaciemnionym ) poprzez równoległość bajtów i spację- kompromisy czasowe .

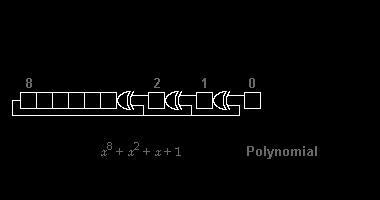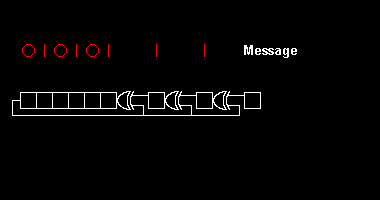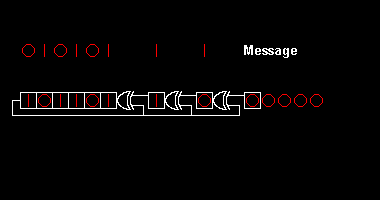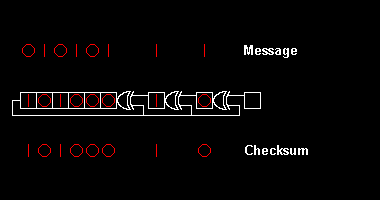
Przykład generowania 8-bitowego CRC . Generator jest rejestrem przesuwnym typu Galois z bramkami XOR umieszczonymi zgodnie z potęgami (białymi liczbami) x w wielomianie generatora. Strumień komunikatów może mieć dowolną długość. Po przejściu przez rejestr, po którym następuje 8 zer, wynikiem w rejestrze jest suma kontrolna.

Sprawdzanie otrzymanych danych za pomocą sumy kontrolnej. Odebrany komunikat jest przesuwany przez ten sam rejestr, co w generatorze, ale zamiast zer dołączana jest do niego otrzymana suma kontrolna. Poprawne dane dają wynik zerowy; uszkodzony bit w komunikacie lub sumie kontrolnej dałby inny wynik, ostrzegając, że wystąpił błąd.

Różne standardy CRC rozszerzają algorytm dzielenia wielomianowego, określając początkową wartość rejestru przesuwnego, końcowy krok Exclusive-Or i, co najważniejsze, kolejność bitów ( endianność ). W rezultacie kod widziany w praktyce łudząco odbiega od „czystego” podziału, a rejestr może przesuwać się w lewo lub w prawo.

Przykład

Jako przykład implementacji dzielenia wielomianowego w sprzęcie, załóżmy, że próbujemy obliczyć 8-bitowy CRC 8-bitowej wiadomości złożonej ze znaku ASCII „W”, który jest binarny 01010111 ₂ , dziesiętny 87 ₁₀ lub szesnastkowy 57 ₁₆ . $_$ użyjemy wielomianu HEC ) Zapisując pierwszy przesłany bit (współczynnik najwyższej potęgi $po$ lewej stronie, odpowiada to 9-bitowemu ciągowi „100000111”.

Wartość bajtu 57 ₁₆ może być przesyłana w dwóch różnych rzędach, w zależności od zastosowanej konwencji porządkowania bitów. Każdy z nich generuje inny wielomian wiadomości ${\ Displaystyle M (x)}$ . Najpierw Msbit, to jest ${\ Displaystyle x ^ {6} + x ^ {4} + x ^ {2} + x + 1}$ = 01010111, podczas gdy lsbit-first , to jest ${\ Displaystyle x ^ {7} + x ^ {6} + x ^ {5} + x ^ {3} + x}$ = 11101010. Te mogą następnie pomnożyć przez ${\ Displaystyle x ^ {8}}$ , aby utworzyć dwa 16-bitowe wielomiany wiadomości ${\ Displaystyle x ^ {8} M (x)}$ .

Obliczenie reszty polega następnie na odjęciu wielokrotności wielomianu generatora sol $\ Displaystyle G (x)}$ . Jest to podobne do dzielenia dziesiętnego, ale jeszcze prostsze, ponieważ jedynymi możliwymi wielokrotnościami na każdym kroku są 0 i 1, a odejmowanie pożycza „od nieskończoności” zamiast zmniejszać górne cyfry. Ponieważ nie dbamy o iloraz, nie ma potrzeby go zapisywać.

Najpierw najbardziej znaczący bit

Najpierw najmniej znaczący bit

	0	1	0	1	0	1	1	1	0	0	0	0	0	0	0	0
−	0	0	0	0	0	0	0	0	0
=	0	1	0	1	0	1	1	1	0	0	0	0	0	0	0	0
	−	1	0	0	0	0	0	1	1	1
=	0	0	0	1	0	1	1	0	1	1	0	0	0	0	0	0
		−	0	0	0	0	0	0	0	0	0
=	0	0	0	1	0	1	1	0	1	1	0	0	0	0	0	0
			−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	1	1	0	1	0	1	1	0	0	0	0
				−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	1	1	0	1	0	1	1	0	0	0	0
					−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	1	0	1	0	1	0	1	1	0	0
						−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	0	0	1	0	1	0	0	0	1	0
							−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	1	0	0	0	1	0

	1	1	1	0	1	0	1	0	0	0	0	0	0	0	0	0
−	1	0	0	0	0	0	1	1	1
=	0	1	1	0	1	0	0	1	1	0	0	0	0	0	0	0
	−	1	0	0	0	0	0	1	1	1
=	0	0	1	0	1	0	0	0	0	1	0	0	0	0	0	0
		−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	1	0	0	0	1	0	1	0	0	0	0	0
			−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	1	0	0	0	1	0	1	0	0	0	0	0
				−	1	0	0	0	0	0	1	1	1
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
					−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
						−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0
							−	0	0	0	0	0	0	0	0	0
=	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0

Zauważ, że po każdym odejmowaniu bity są dzielone na trzy grupy: na początku grupa, w której wszystkie są zerowe; na koniec grupa niezmieniona w stosunku do oryginału; i niebieska zacieniona grupa pośrodku, która jest „interesująca”. „Interesująca” grupa ma długość 8 bitów, co odpowiada stopniowi wielomianu. Na każdym kroku odejmuje się odpowiednią wielokrotność wielomianu, aby grupa zerowa była o jeden bit dłuższa, a niezmieniona grupa stawała się o jeden bit krótsza, aż zostanie tylko ostatnia reszta.

W przykładzie msbit-first wielomian reszty to ${\ Displaystyle x ^ {7} + x ^ {5} + x}$ . Konwersja na liczbę szesnastkową przy użyciu konwencji, że najwyższą potęgą x jest msbit; to jest A2 ₁₆ . W lsbit-first, reszta to ${\ Displaystyle x ^ {7} + x ^ {4} + x ^ {3}}$ . Konwersja na szesnastkowy przy użyciu konwencji, że najwyższą potęgą x jest lsbit, to jest 19 ₁₆ .

Realizacja

Pisanie pełnej wiadomości na każdym kroku, jak w powyższym przykładzie, jest bardzo uciążliwe. Wydajne implementacje wykorzystują $do$ rejestr przesuwny przechowywania tylko interesujących bitów. Mnożenie wielomianu przez $jedno$ miejsce, ponieważ współczynniki nie zmieniają wartości, a jedynie przesuwają się w górę do następnego wyrazu wielomianu.

Oto pierwszy szkic pseudokodu do obliczania n -bitowego CRC. Wykorzystuje wymyślony złożony typ danych dla wielomianów, gdzie x nie jest zmienną całkowitą, ale konstruktorem generującym obiekt wielomianu , który można dodawać, mnożyć i potęgować. Xor to dodać je, modulo dwa; to znaczy, aby wykluczyć LUB współczynniki każdego pasującego terminu z obu wielomianów.

    
    ⁰   
        
     function  crc(  tablica bitów  bitString[1..len],  int  len) { resztaPolynomial :=  polynomialForm  (bitString[1..n])  // Pierwszych n bitów wiadomości  // Popularny wariant uzupełnia tutaj resztaPolynomial; patrz   § Preset na −1  poniżej  dla  i  od  1  do  len {reszta wielomianu := reszta wielomianu *  x  + bitString[i+n] *  x  // Zdefiniuj bitString[k]=0 dla k>len  jeśli  współczynnik  x ⁿ reszty wielomianu = 1 {reszta wielomianu := reszta wielomianu  xor  generatorPolynomial } }  // Popularny wariant uzupełnia tutaj resztę wielomianu; zobacz   § Post-odwróć  poniżej  return  resztaWielomian }

Fragment kodu 1: Proste dzielenie wielomianowe

Należy zauważyć, że ten przykładowy kod pozwala uniknąć konieczności określania konwencji porządkowania bitów przez nieużywanie bajtów; wejściowy bitString jest już w postaci tablicy bitów, a pozostała część Wielomian jest manipulowana w kategoriach operacji wielomianowych; mnożenie przez $w$ prawo, a dodanie ${\ displaystyle x }$ [i + n] jest wykonywane do współczynnika, który może być prawy lub lewy koniec rejestru.

Ten kod ma dwie wady. Po pierwsze, $w$ wymaga rejestru n + 1-bitowego do przechowywania pozostałego wielomianu aby można było przetestować współczynnik. Co ważniejsze, wymaga dopełnienia bitString n bitami zerowymi.

$displaystyle x ^$ można rozwiązać, testując współczynnik reszty wielomianu przed pomnożeniem go przez ${n-1}$ }

Drugi problem można rozwiązać, wykonując ostatnie n iteracji inaczej, ale istnieje bardziej subtelna optymalizacja, która jest stosowana powszechnie, zarówno w implementacjach sprzętowych, jak i programowych.

Ponieważ operacja XOR używana do odejmowania wielomianu generatora od komunikatu jest przemienna i asocjacyjna , nie ma znaczenia, w jakiej kolejności różne dane wejściowe są łączone w pozostałą część wielomianu . A dokładniej, danego bitu bitString nie trzeba dodawać do resztyPolynomial aż do ostatniej chwili, kiedy jest testowany w celu ustalenia, czy należy xorować za pomocą generatorPolynomial .

Eliminuje to również konieczność wstępnego ładowania pozostałego wielomianu z pierwszymi n bitami wiadomości:

    
     function  crc(  tablica bitów  bitString[1..len],  int  len) {resztaPolynomial := 0  // Popularny wariant uzupełnia tutaj resztęPolynomial; patrz   § Preset na −1  poniżej  dla  i  od  1  do  len {reszta Wielomianu := reszta Wielomianu  xor  (ciąg bitów [i] *  x ⁿ⁻¹ )  if  (współczynnik  x ⁿ⁻¹ reszty Wielomianu) = 1 { reszta Wielomianu := (reszta Wielomianu *  x  )  xor  generatorPolynomial }  else  {resztaPolynomial := (remainderPolynomial *  x  ) } } }  // Popularny wariant uzupełnia tutaj resztaPolynomial; patrz   § Post-invert  poniżej  return  resztaWielomian }

Fragment kodu 2: Dzielenie wielomianu z odroczoną wiadomością XOR

Jest to standardowa sprzętowa implementacja CRC typu „bit-at-a-time” i jest warta przestudiowania; kiedy zrozumiesz, dlaczego to oblicza dokładnie taki sam wynik jak pierwsza wersja, pozostałe optymalizacje są dość proste. Jeśli reszta wielomianu $ma$ tylko n bitów długości, to współczynniki tego i wielomianu generatora są po odrzucane To jest powód, dla którego zwykle zobaczysz wielomiany CRC zapisane binarnie z pominięciem wiodącego współczynnika.

W oprogramowaniu wygodnie jest zauważyć, że chociaż można opóźnić xor każdego bitu do ostatniej chwili, można to również zrobić wcześniej. Zwykle wygodnie jest wykonywać xor bajt po bajcie, nawet w implementacji typu bit-a-time, takiej jak ta :

     
        
            
     function  crc(  byte array  string[1..len],  int  len) {resztaPolynomial := 0  // Popularny wariant uzupełnia tutaj resztęPolynomial; patrz   § Preset to −1  poniżej  dla  i  od  1  do  len {reszta wielomianu := reszta wielomianu  xor  polynomialForm  (string[i]) * x ⁿ⁻⁸ dla  j  od  1  do  8 {  // Zakładając 8 bitów na bajt,  jeśli  współczynnik  x ^{n −1} z reszty Wielomianu = 1 { reszta Wielomianu := (reszta Wielomianu *  x  )  xor  generator Wielomianu }  else  { reszta Wielomianu := (reszta Wielomianu *  x  ) } } }  // Popularny wariant uzupełnia tutaj resztę Wielomianu; patrz   § Post-invert  poniżej  return  resztaWielomian }

Fragment kodu 3: Dzielenie wielomianowe z komunikatem XORing po bajtach

Jest to zwykle najbardziej kompaktowa implementacja oprogramowania, stosowana w mikrokontrolerach , gdy przestrzeń jest ważniejsza niż prędkość.

Kolejność bitów (endianowość)

Po zaimplementowaniu w sprzęcie szeregowym bitowym wielomian generatora jednoznacznie opisuje przypisanie bitów; pierwszy transmitowany bit jest zawsze współczynnikiem najwyższej potęgi , a ostatnie $transmitowane$ to reszta CRC , $zaczynając$ od $Displaystyle R (x)}$ współczynnik $}}$ $1$ i kończący się współczynnikiem , czyli współczynnikiem 1.

Jednak gdy bity są przetwarzane bajt po bajcie, na przykład podczas transmisji równoległej , ramek bajtów, jak w kodowaniu 8B/10B lub asynchronicznej komunikacji szeregowej w stylu RS-232 , lub podczas implementacji CRC w oprogramowaniu , konieczne jest określenie kolejność bitów (endianowość) danych; który bit w każdym bajcie jest uważany za „pierwszy” i będzie współczynnikiem wyższej potęgi ${\ displaystyle x}$ .

Jeśli dane są przeznaczone do komunikacji szeregowej , najlepiej jest użyć kolejności bitów, w której dane zostaną ostatecznie wysłane. Dzieje się tak, ponieważ zdolność CRC do wykrywania błędów serii jest oparta na bliskości wielomianu wiadomości ${\ displaystyle M(x)}$ ; jeśli sąsiednie wyrażenia wielomianowe nie są przesyłane sekwencyjnie, seria błędów fizycznych o jednej długości może być postrzegana jako seria dłuższa z powodu przegrupowania bitów.

Na przykład zarówno standardy IEEE 802 (ethernet), jak i RS - 232 ( port szeregowy ) określają transmisję z najmniej znaczącym bitem (little-endian), więc programowa implementacja CRC do ochrony danych przesyłanych przez takie łącze powinna mapować najmniej znaczące bity w każdym bajcie do współczynników o najwyższych potęgach ${\ displaystyle x}$ . Z drugiej strony dyskietki i większość dysków twardych najpierw zapisuje najbardziej znaczący bit każdego bajtu.

CRC lsbit-first jest nieco prostszy do zaimplementowania w oprogramowaniu, więc jest nieco częściej spotykany, ale wielu programistów uważa, że kolejność msbit-first bit jest łatwiejsza do naśladowania. Tak więc, na przykład, XMODEM -CRC, wczesne użycie CRC w oprogramowaniu, wykorzystuje msbit-first CRC.

$,$ opisując przesunięcia w pseudokodzie jako mnożenia przez zapisując wyraźne konwersje z postaci binarnej na wielomianową. W praktyce CRC jest przechowywany w standardowym rejestrze binarnym przy użyciu określonej konwencji porządkowania bitów. W postaci pierwszego bitu najbardziej znaczące bity binarne będą wysyłane jako pierwsze i zawierają współczynniki wielomianu wyższego rzędu, podczas gdy w postaci pierwszego bitu najmniej znaczące bity binarne zawierają współczynniki wyższego rzędu. Powyższy pseudokod można zapisać w obu formach. Dla konkretności wykorzystuje to 16-bitowy wielomian CRC-16- CCITT : ${\ Displaystyle x ^ {16} + x ^ {12} + x ^ {5} + 1$ }



    
        
            
     // Najpierw najbardziej znaczący bit (big-endian)  // x^16+x^12+x^5+1 = (1) 0001 0000 0010 0001 = 0x1021  function  crc(  byte array  string[1..len],  int  len) { rem := 0  // Popularny wariant uzupełnia rem tutaj  dla  i  od  1  do  len { rem := rem  xor  (string[i]  leftShift  (n-8))  // n = 16 w tym przykładzie  dla  j  od  1  do  8 {  // Zakładając 8 bitów na bajt  , jeśli  rem  i  0x8000 {  // jeśli ustawiony jest najbardziej lewy (najbardziej znaczący) bit  rem := (rem  leftShift  1)  xor  0x1021 }  else  { rem := rem  leftShift  1 } rem := rem  i  0xffff // Przytnij resztę do 16 bitów } }  // Popularny wariant uzupełnia tutaj rem  return  rem }

Fragment kodu 4: Dzielenie oparte na rejestrze przesuwnym, najpierw MSB



    
            
     // Najpierw najmniej znaczący bit (little-endian)  // x^16 +x^12+x^5+1 = 1000 0100 0000 1000 (1) = 0x8408  function  crc(  byte array  string[1..len],  int  len) { rem := 0  // Popularny wariant uzupełnia rem tutaj  dla  i  od  1  do  len { rem := rem  xor  string[i]  for  j  od  1  do  8 {  // Zakładając 8 bitów na bajt  , jeśli  rem  i  0x0001 {  // jeśli ustawiony jest prawy (najbardziej znaczący) bit  rem := (rem  rightShift  1)  xor  0x8408 }  else  { rem := rem  rightShift  1 } } }  // Popularny wariant uzupełnia rem tutaj  return  rem }

Fragment kodu 5: Dzielenie oparte na rejestrze przesuwnym, najpierw LSB

Zauważ, że forma lsbit-first pozwala uniknąć konieczności przesuwania string[i] przed xor . W obu przypadkach pamiętaj o przesyłaniu bajtów CRC w kolejności zgodnej z wybraną konwencją porządkowania bitów.

Obliczenia wielobitowe

Algorytm Sarwate (pojedyncza tabela przeglądowa)

Inna powszechna optymalizacja wykorzystuje tablicę przeglądową indeksowaną przez współczynniki rem najwyższego rzędu do przetwarzania więcej niż jednego bitu dywidendy na iterację. Najczęściej używana jest tablica przeglądowa zawierająca 256 wpisów, zastępując treść zewnętrznej pętli (nad i ) przez:

 // Msbit-first rem = (rem  leftShift  8)  xor  big_endian_table[string[i]  xor  ((ostatnie lewe 8 bitów rem)  rightShift  (n-8))] // Lsbit-first rem = (rem  rightShift  8)  xor  little_endian_table [string[i]  xor  (8 najbardziej wysuniętych na prawo bitów rem)]

Fragment kodu 6: Rdzenie podziału opartego na tabelach

Jeden z najczęściej spotykanych algorytmów CRC jest znany jako CRC-32 , używany (między innymi) przez Ethernet , FDDI , ZIP i inne formaty archiwów oraz format obrazów PNG . Jego wielomian można zapisać najpierw msbit jako 0x04C11DB7 lub najpierw lsbit jako 0xEDB88320. Strona internetowa W3C w PNG zawiera dodatek z krótką i prostą implementacją opartą na tabelach w C CRC-32. Zauważysz, że kod odpowiada przedstawionemu tutaj pseudokodowi lsbit-first bajt-a-czasu, a tabela jest generowana przy użyciu kodu bit-at-a-time.

Zwykle najwygodniejszy jest stół z 256 wpisami, ale można użyć innych rozmiarów. W małych mikrokontrolerach użycie 16-wejściowej tablicy do przetwarzania czterech bitów jednocześnie daje użyteczną poprawę szybkości przy jednoczesnym zachowaniu niewielkich rozmiarów tablicy. Na komputerach z dużą ilością pamięci 65 536 wpisów może służyć do jednoczesnego przetwarzania 16 bitów.

Generowanie tabel

Oprogramowanie do generowania tabel jest tak małe i szybkie, że zwykle szybciej jest je obliczyć podczas uruchamiania programu niż ładować wstępnie obliczone tabele z pamięci. Jedną z popularnych technik jest użycie kodu bit-at-a-time 256 razy w celu wygenerowania CRC z 256 możliwych 8-bitowych bajtów. Można to jednak znacznie zoptymalizować, korzystając z właściwości table[i xor j] == table[i] xor table[j] . Tylko wpisy w tabeli odpowiadające potęgom dwójki muszą być obliczane bezpośrednio.

W poniższym przykładowym kodzie crc przechowuje wartość table[i] :

     0  big_endian_table[0] := 0 crc := 0x8000 //  Zakładając 16-bitowy wielomian  i := 1  do  {  if  crc  i  0x8000 { crc := (crc  leftShift  1)  xor  0x1021 //  Wielomian CRC  }  else  { crc : = crc  leftShift  1 } // crc  jest wartością  big_endian_table[i]  ; niech   j  iteruje po już zainicjowanych wpisach  dla  j  od  do  i−1 { big_endian_table[i + j] := crc  xor  big_endian_table[j]; } i := i   przesunięcie w lewo  1 }  while  i < 256

Fragment kodu 7: Generowanie tablicy CRC bajt-po-czasie, najpierw MSB

     0  little_endian_table[0] := 0 crc := 1; i := 128   do  {  if  crc  i  1 { crc := (crc  rightShift  1)  xor  0x8408 //  Wielomian CRC  }  else  { crc := crc  rightShift  1 } // crc  jest wartością  little_endian_table[i]  ; niech   j  iteruje po już zainicjowanych wpisach  dla  j  od  do  255  przez  2 × i { little_endian_table[i + j] := crc  xor  little_endian_table[j]; } i := i   przesunięcie w prawo  1 }  while  i > 0

Fragment kodu 8: Generowanie tablicy CRC bajt-po-czasie, najpierw LSB

W tych przykładach kodu indeks tabeli i + j jest równoważny z i xor j ; możesz użyć dowolnej formy, która jest dla Ciebie wygodniejsza.

Podział bajtów przy użyciu wielu tabel

Istnieje algorytm krojenia po N (zwykle krojenie po 8 dla CRC32; N ≤ 64), który zwykle podwaja lub potraja wydajność w porównaniu z algorytmem Sarwate. Zamiast odczytywać 8 bitów na raz, algorytm odczytuje 8N bitów na raz. W ten sposób maksymalizuje się wydajność superskalarnych .

Nie jest jasne, kto faktycznie wynalazł algorytm.

Obliczenia równoległe bez tabeli

Aktualizacja równoległa dla bajtu lub słowa na raz może być również wykonana jawnie, bez tabeli. Jest to zwykle używane w szybkich implementacjach sprzętowych. Dla każdego bitu rozwiązywane jest równanie po przesunięciu 8 bitów. Poniższe tabele zawierają równania dla niektórych powszechnie używanych wielomianów, używając następujących symboli:

c _ja	Bit CRC 7…0 (lub 15…0) przed aktualizacją
r _ja	Bit CRC 7…0 (lub 15…0) po aktualizacji
d _ja	bit danych wejściowych 7…0
mi _ja = re _ja + do _ja	₀ e _p = e ₇ + e ₆ + … + e ₁ + e (bit parzystości)
s _ja = re _ja + do _{ja + 8}	₀ s _p = s ₇ + s ₆ + … + s ₁ + s (bit parzystości)

Bitowe równania aktualizacji dla niektórych wielomianów CRC-8 po przesunięciu 8 bitów
Wielomian:	( x ⁷ + x ³ + 1) × x (przesunięty w lewo CRC-7-CCITT)	x ⁸ + x ⁵ + x ⁴ + 1 (CRC-8-Dallas/Maxim)
Współczynniki:	0x12 = (0x09 << 1) ( MSBF /normalny)	0x8c ( LSBF /rewers)
₀ r ← r ₁ ← r ₂ ← r ₃ ← r ₄ ← r ₅ ← r ₆ ← r ₇ ←	₀ ₀ 0 mi + mi ₄ + mi ₇ mi ₁ + mi ₅ mi ₂ + mi ₆ mi ₃ + mi ₇ + mi + mi ₄ + mi _{7 mi}₄ + mi ₁ + mi ₅ mi ₅ + mi ₂ + mi ₆ mi ₆ + mi ₃ + mi ₇	₀ ₀ ₀ ₀₀ ₀₀ mi + mi ₄ + mi ₁ + mi + mi ₅ + mi ₂ + mi ₁ mi ₁ + mi ₅ + mi ₂ + mi ₁ + mi ₆ + mi 3 + mi ₂ + mi mi ₂ + mi ₆ + mi ₃₊ mi ₂ + mi + mi ₇ + mi ₄ + mi ₃ + mi ₁ mi ₃ + mi + mi ₇ + mi ₄ + mi ₃ + mi ₁ mi ₄ + mi ₁ + mi mi ₅ + mi ₂ + mi ₁ mi ₆ + mi ₃ + mi ₂ + mi mi ₇ + mi ₄ + mi ₃ + mi ₁
Fragmenty kodu C :	uint8_t c , re , mi , fa , r ; … mi = do ^ re ; fa = mi ^ ( mi >> 4 ) ^ ( mi >> 7 ); r = ( fa << 1 ) ^ ( fa << 4 );	uint8_t c , re , mi , fa , r ; … mi = do ^ re ; fa = mi ^ ( mi << 3 ) ^ ( mi << 4 ) ^ ( mi << 6 ); r = fa ^ ( fa >> 4 ) ^ ( fa >> 5 );

Bitowe równania aktualizacji dla niektórych wielomianów CRC-16 po przesunięciu 8 bitów
Wielomian:	x ¹⁶ + x ¹² + x ⁵ + 1 (CRC-16-CCITT)		x ¹⁶ + x ¹⁵ + x ² + 1 (CRC-16-ANSI)
Współczynniki:	0x1021 (MSBF/normalny)	0x8408 (LSBF/wsteczny)	0x8005 (MSBF/normalny)	0xa001 (LSBF/wsteczny)
₀ r ← r ₁ ← r ₂ ← r ₃ ← r ₄ ← r ₅ ← r ₆ ← r ₇ ← r ₈ ← r ₉_← r ₁₀ ← r ₁₁ ← r ₁₂ ← r 13 ← r ₁₄ ← r ₁₅ ←	₀ ₀ ₀ ₀ s ₄ + s s ₅ + s ₁ s ₆ + s ₂ s ₇ + s ₃ s ₄ s ₅ + s ₄ + s s ₆ + s ₅ + s ₁ s _{7 + s 6}₊ s 2 _do + s ₇ + s ₃ do ₁ + s ₄ do ₂ + s ₅ do ₃ + s ₆ do ₄ + s ₇ + s ₄ + s do ₅ + s ₅ + s ₁ do ₆ + s ₆ + s ₂ do ₇ + s ₇ + s ₃	₀ ₀ ₀ ₀ ₀ do ₈ + mi ₄ + mi do ₉ + mi ₅ + mi ₁ do ₁₀ + mi ₆ + mi ₂ do ₁₁ + mi + mi ₇ + mi ₃ do ₁₂ + mi ₁ do ₁₃ + mi 2 _do₁₄ + mi 3 _do₁₅ + mi ₄ + mi mi + mi ₅ + mi ₁ mi ₁ + mi ₆ + mi ₂ mi ₂ + mi ₇ + mi ₃ mi ₃ mi ₄ + mi mi ₅ + mi ₁ mi ₆ + mi ₂ mi ₇ + mi ₃	₀ ₀ ₀ s _p s + s _p s ₁ + s s ₂ + s ₁ s ₃ + s ₂ s ₄ + s ₃ s ₅ + s ₄ s ₆ + s ₅ do + s ₇ + s ₆ do ₁ + s ₇ do ₂ do ₃ do ₄ do ₅ do ₆ do ₇ + s _str	₀₀ do ₈ + e _p do ₉ do ₁₀ do ₁₁ do ₁₂ do ₁₃ do ₁₄ + mi do ₁₅ + mi ₁ + mi mi ₂ + mi ₁ mi ₃ + mi ₂ mi ₄ + mi ₃ mi ₅ + mi ₄ mi ₆ + mi ₅ mi ₇ + mi ₆ mi _p + mi ₇ mi _s
Fragmenty kodu C :	uint8_t re , s , t ; uint16_t c , r ; … s = re ^ ( do >> 8 ); t = s ^ ( s >> 4 ); r = ( do << 8 ) ^ t ^ ( t << 5 ) ^ ( t << 12 );	uint8_t d , e , f ; uint16_t c , r ; … mi = do ^ re ; fa = mi ^ ( mi << 4 ); r = ( do >> 8 ) ^ ( fa << 8 ) ^ ( fa << 3 ) ^ ( fa >> 4 );	uint8_t re , s , p ; uint16_t c , r , t ; … s = re ^ ( do >> 8 ); p = s ^ ( s >> 4 ); p = p ^ ( p >> 2 ); p = p ^ ( p >> 1 ); p = p & 1 ; t = p \| ( s << 1 ); r = ( do << 8 ) ^ ( t << 15 ) ^ t ^ ( t << 1 );	uint8_t d , e , p ; uint16_t c , r , f ; … mi = do ^ re ; p = mi ^ ( mi >> 4 ); p = p ^ ( p >> 2 ); p = p ^ ( p >> 1 ); p = p & 1 ; fa = mi \| ( p << 8 ); r = ( do >> 8 ) ^ ( fa << 6 ) ^ ( fa << 7 ) ^ ( fa >> 8 );

Obliczenia dwuetapowe

Ponieważ wielomian CRC-32 ma dużą liczbę składników, podczas obliczania reszty po bajcie na raz każdy bit zależy od kilku bitów poprzedniej iteracji. W sprzętowych implementacjach bajtowo-równoległych wymaga to bramek XOR z wieloma wejściami lub kaskadowych, co zwiększa opóźnienie propagacji .

Aby zmaksymalizować szybkość obliczeń, resztę pośrednią można obliczyć, przepuszczając wiadomość przez 123-bitowy rejestr przesuwny. Wielomian jest starannie dobraną wielokrotnością standardowego wielomianu, tak że terminy (odbiory sprzężenia zwrotnego) są szeroko rozstawione, a żaden bit pozostałej części nie jest poddawany operacji XOR więcej niż raz na iterację bajtu. Potrzebne są więc tylko dwuwejściowe bramki XOR, możliwie najszybsze. Ostatecznie reszta pośrednia jest dzielona przez standardowy wielomian w drugim rejestrze przesuwnym, aby uzyskać resztę CRC-32.

Obliczenia blokowe

Blokowe obliczenie reszty można wykonać sprzętowo dla dowolnego wielomianu CRC, rozkładając na czynniki macierz transformacji przestrzeni stanów potrzebną do obliczenia reszty na dwie prostsze macierze Toeplitza.

Jednoprzebiegowa kontrola

Podczas dołączania CRC do wiadomości, możliwe jest odłączenie przesyłanego CRC, ponowne obliczenie i zweryfikowanie przeliczonej wartości z przesłaną. Jednak prostsza technika jest powszechnie stosowana w sprzęcie.

Kiedy CRC jest przesyłane z prawidłową kolejnością bajtów (zgodną z wybraną konwencją porządkowania bitów), odbiornik może obliczyć całkowitą CRC na podstawie wiadomości i CRC, a jeśli są poprawne, wynik będzie równy zero. Ta możliwość jest powodem, dla którego większość protokołów sieciowych zawierających CRC robi to przed końcowym ogranicznikiem; nie trzeba wiedzieć, czy zbliża się koniec pakietu, aby sprawdzić CRC.

warianty CRC

W praktyce większość standardów określa ustawienie rejestru na wszystkie jedynki i odwrócenie CRC przed transmisją. Nie ma to wpływu na zdolność CRC do wykrywania zmienionych bitów, ale daje mu możliwość zauważenia bitów dodanych do wiadomości.

Wstępnie ustawione na −1

Podstawowa matematyka CRC akceptuje (uważa za poprawnie przesłane) komunikaty, które interpretowane jako wielomian są wielokrotnością wielomianu CRC. Jeśli do takiego komunikatu dołączy się kilka początkowych bitów 0, nie zmienią one jego interpretacji jako wielomianu. Jest to równoważne z faktem, że 0001 i 1 to ta sama liczba.

Ale jeśli przesyłanej wiadomości zależy na początkowych bitach 0, niezdolność podstawowego algorytmu CRC do wykrycia takiej zmiany jest niepożądana. Jeśli jest możliwe, że błąd transmisji mógłby dodać takie bity, prostym rozwiązaniem jest rozpoczęcie od rejestru rem ustawionego na jakąś niezerową wartość; dla wygody zwykle używana jest wartość all-one. Jest to matematycznie równoważne z uzupełnieniem (binarnym NOT) pierwszych n bitów wiadomości, gdzie n jest liczbą bitów w rejestrze CRC.

Nie wpływa to w żaden sposób na generowanie i sprawdzanie CRC, o ile zarówno generator, jak i kontroler używają tej samej wartości początkowej. Dowolna niezerowa wartość początkowa wystarczy, a kilka standardów określa nietypowe wartości, ale wartość zerowa (-1 w systemie binarnym dopełnienia do dwóch) jest zdecydowanie najczęstsza. Należy zauważyć, że jednoprzebiegowe generowanie/sprawdzanie CRC nadal będzie dawać wynik zerowy, gdy komunikat jest poprawny, niezależnie od ustawionej wartości.

Po odwróceniu

Ten sam rodzaj błędu może wystąpić na końcu komunikatu, aczkolwiek w przypadku bardziej ograniczonego zestawu komunikatów. Dodanie 0 bitów do wiadomości jest równoważne pomnożeniu jej wielomianu przez x , a jeśli wcześniej był to wielokrotność wielomianu CRC, wynik tego mnożenia również będzie taki sam. Jest to równoważne z faktem, że ponieważ 726 jest wielokrotnością 11, więc jest 7260.

Podobne rozwiązanie można zastosować na końcu komunikatu, odwracając rejestr CRC przed jego dołączeniem do komunikatu. Ponownie wystarczy każda niezerowa zmiana; odwrócenie wszystkich bitów (XORing ze wzorcem all-one) jest po prostu najczęstsze.

Ma to wpływ na jednoprzebiegowe sprawdzanie CRC: zamiast generowania wyniku zerowego, gdy komunikat jest poprawny, daje stały wynik niezerowy. (Ściślej mówiąc, wynikiem jest CRC (bez niezerowego ustawienia wstępnego, ale z post-odwróceniem) wzorca inwersji). dowolny komunikat), można go użyć bezpośrednio do weryfikacji poprawności dowolnego innego komunikatu sprawdzanego przy użyciu tego samego algorytmu CRC.

Zobacz też

Kategoria ogólna

Kod poprawiający błąd
Lista funkcji skrótu
Parzystość odpowiada 1-bitowemu CRC z wielomianem $x +1$ .

Sumy kontrolne inne niż CRC

^ Dubrowa, Elena; Mansouri, Shohreh Sharif (maj 2012). „Podejście oparte na BDD do konstruowania LFSR do równoległego kodowania CRC” . Proceedings of IEEE International Symposium on Multiple-Valued Logic : 128–133. doi : 10.1109/ISMVL.2012.20 . ISBN 978-0-7695-4673-5 . S2CID 27306826 .
^ ^a ^b Williams, Ross N. (24.09.1996). „Bezbolesny przewodnik po algorytmach wykrywania błędów CRC, wersja 3.00” . Zarchiwizowane od oryginału w dniu 2006-09-27 . Źródło 2016-02-16 .
^ Sarwate, Dilip V. (sierpień 1998). „Obliczanie cyklicznych kontroli redundancji za pomocą wyszukiwania w tabeli” . Komunikaty ACM . 31 (8): 1008–1013. doi : 10.1145/63030.63037 . S2CID 5363350 .
^ „Specyfikacja przenośnej grafiki sieciowej (PNG) (wydanie drugie): załącznik D, przykładowa implementacja kodu cyklicznej nadmiarowości” . W3C . 2003-11-10 . Źródło 2016-02-16 .
^ Kounavis, Michael E.; Berry, Frank L. (27–30 czerwca 2005). Systematyczne podejście do budowania wysokowydajnych, opartych na oprogramowaniu generatorów CRC (PDF) . Sympozjum IEEE 2013 na temat komputerów i komunikacji (ISCC). Cartagena, Murcja, Hiszpania. s. 855–862. doi : 10.1109/ISCC.2005.18 . ISBN 0-7695-2373-0 .
Bibliografia _ Kounavis, Michael E. (listopad 2008). „Nowe algorytmy oparte na wyszukiwaniu w tabeli do wysokowydajnego generowania CRC” . Transakcje IEEE na komputerach . 57 (11): 1550-1560. doi : 10.1109/TC.2008.85 . S2CID 206624854 .
^ Generowanie CRC o wysokiej liczbie oktanowej z algorytmem Intel Slicing-by-8 (PDF) (raport techniczny). Intel . Zarchiwizowane od oryginału (PDF) w dniu 22.07.2012.
^ „Krótki samouczek dotyczący obliczania CRC” . Archiwa jądra Linuksa .
^ Menon-Sen, Abhijit (20.01.2017). „Kto wynalazł algorytm slicing-by-N CRC32?” .
^ Jon Buller (15.03.1996). „Re: 8051 i CRC-CCITT” . Grupa dyskusyjna : comp.arch.embedded . Usenet: [email protected] . Źródło 2016-02-16 .
^ Glaise, René J. (1997-01-20). „Dwuetapowe obliczenie kodu cyklicznej redundancji CRC-32 dla sieci ATM” . IBM Journal of Research and Development . Armonk, Nowy Jork : IBM . 41 (6): 705. doi : 10.1147/rd.416.0705 . Zarchiwizowane od oryginału w dniu 2009-01-30 . Źródło 2016-02-16 .
^ Das, Arindam (2022). „Obliczanie blokowe kodu cyklicznej redundancji przy użyciu faktoryzowanych macierzy Toeplitza zamiast tabeli przeglądowej” . Transakcje IEEE na komputerach : 1–12. doi : 10.1109/TC.2022.3189574 . ISSN 0018-9340 . S2CID 250472783 .
^ Np . karta katalogowa (PDF) , Texas Instruments , listopad 2009, s. 39 , dostęp 2016-02-16 , Generator CRC jest inicjowany wartością 0x3791, jak pokazano na rysunku 50. RFID TMS37157 o niskiej częstotliwości - pasywne urządzenie interfejsu niskiej częstotliwości z pamięcią EEPROM i interfejsem transpondera 134,2 kHz

Linki zewnętrzne

Jan Paweł Adamowski. „64-bitowy cykliczny nadmiarowy kod - długie dzielenie XOR na bajtowe wyszukiwanie w tabeli” .

Andrew Kadarcha, Boba Jenkinsa. „Wydajna (~ 1 cykl procesora na bajt) implementacja CRC” . GitHub .

[1] Dubrowa, Elena; Mansouri, Shohreh Sharif (maj 2012). „Podejście oparte na BDD do konstruowania LFSR do równoległego kodowania CRC” . Proceedings of IEEE International Symposium on Multiple-Valued Logic : 128–133. doi : 10.1109/ISMVL.2012.20 . ISBN 978-0-7695-4673-5 . S2CID 27306826 .

[williams96-2] Williams, Ross N. (24.09.1996). „Bezbolesny przewodnik po algorytmach wykrywania błędów CRC, wersja 3.00” . Zarchiwizowane od oryginału w dniu 2006-09-27 . Źródło 2016-02-16 .

[3] Sarwate, Dilip V. (sierpień 1998). „Obliczanie cyklicznych kontroli redundancji za pomocą wyszukiwania w tabeli” . Komunikaty ACM . 31 (8): 1008–1013. doi : 10.1145/63030.63037 . S2CID 5363350 .

[4] „Specyfikacja przenośnej grafiki sieciowej (PNG) (wydanie drugie): załącznik D, przykładowa implementacja kodu cyklicznej nadmiarowości” . W3C . 2003-11-10 . Źródło 2016-02-16 .

[5] Kounavis, Michael E.; Berry, Frank L. (27–30 czerwca 2005). Systematyczne podejście do budowania wysokowydajnych, opartych na oprogramowaniu generatorów CRC (PDF) . Sympozjum IEEE 2013 na temat komputerów i komunikacji (ISCC). Cartagena, Murcja, Hiszpania. s. 855–862. doi : 10.1109/ISCC.2005.18 . ISBN 0-7695-2373-0 .

[6] Bibliografia _ Kounavis, Michael E. (listopad 2008). „Nowe algorytmy oparte na wyszukiwaniu w tabeli do wysokowydajnego generowania CRC” . Transakcje IEEE na komputerach . 57 (11): 1550-1560. doi : 10.1109/TC.2008.85 . S2CID 206624854 .

[7] Generowanie CRC o wysokiej liczbie oktanowej z algorytmem Intel Slicing-by-8 (PDF) (raport techniczny). Intel . Zarchiwizowane od oryginału (PDF) w dniu 22.07.2012.

[8] „Krótki samouczek dotyczący obliczania CRC” . Archiwa jądra Linuksa .

[9] Menon-Sen, Abhijit (20.01.2017). „Kto wynalazł algorytm slicing-by-N CRC32?” .

[10] Jon Buller (15.03.1996). „Re: 8051 i CRC-CCITT” . Grupa dyskusyjna : comp.arch.embedded . Usenet: [email protected] . Źródło 2016-02-16 .

[glaise-11] Glaise, René J. (1997-01-20). „Dwuetapowe obliczenie kodu cyklicznej redundancji CRC-32 dla sieci ATM” . IBM Journal of Research and Development . Armonk, Nowy Jork : IBM . 41 (6): 705. doi : 10.1147/rd.416.0705 . Zarchiwizowane od oryginału w dniu 2009-01-30 . Źródło 2016-02-16 .

[12] Das, Arindam (2022). „Obliczanie blokowe kodu cyklicznej redundancji przy użyciu faktoryzowanych macierzy Toeplitza zamiast tabeli przeglądowej” . Transakcje IEEE na komputerach : 1–12. doi : 10.1109/TC.2022.3189574 . ISSN 0018-9340 . S2CID 250472783 .

[13] ^ Np . karta katalogowa (PDF) , Texas Instruments , listopad 2009, s. 39 , dostęp 2016-02-16 , Generator CRC jest inicjowany wartością 0x3791, jak pokazano na rysunku 50. RFID TMS37157 o niskiej częstotliwości - pasywne urządzenie interfejsu niskiej częstotliwości z pamięcią EEPROM i interfejsem transpondera 134,2 kHz