Obliczenia membranowe
Obliczenia membranowe (lub MC ) to dziedzina informatyki , której celem jest odkrycie nowych modeli obliczeniowych na podstawie badań komórek biologicznych , zwłaszcza błon komórkowych . Jest to podzadanie tworzenia modelu komórkowego .
Obliczenia membranowe zajmują się rozproszonymi i równoległymi modelami obliczeniowymi, przetwarzając wielozbiory obiektów symboli w sposób zlokalizowany. W ten sposób zasady ewolucji pozwalają na zamknięcie ewoluujących obiektów w przedziałach określonych przez membrany. Istotną rolę w tych procesach odgrywa komunikacja między przedziałami oraz z otoczeniem. Różne typy systemów membranowych są znane jako systemy P na cześć Gheorghe Păuna , który jako pierwszy wymyślił model w 1998 roku.
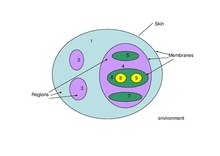
Istotnym składnikiem systemu P jest jego struktura membranowa, którą może być hierarchiczny układ membran, jak w komórce, lub sieć membran (umieszczonych w węzłach grafu), jak w tkance lub sieci neuronowej. Systemy P są często przedstawiane graficznie z rysunkami.
Intuicja stojąca za pojęciem błony to trójwymiarowy pęcherzyk z biologii. Jednak sama koncepcja jest bardziej ogólna, a membrana jest postrzegana jako separator dwóch regionów. Membrana zapewnia selektywną komunikację między dwoma regionami. Według Gheorghe Păuna następuje podział przestrzeni euklidesowej na skończone „wewnętrzne” i nieskończone „zewnętrzne”. Selektywna komunikacja to miejsce, w którym pojawia się przetwarzanie.
Reprezentacje graficzne mogą zawierać wiele elementów, w zależności od odmiany badanego modelu. Na przykład reguła może generować specjalny symbol δ, w którym to przypadku zawierająca ją membrana ulega rozpuszczeniu, a cała jej zawartość przesuwa się wyżej w hierarchii regionu.
Różnorodność sugestii płynących z biologii oraz zakres możliwości definiowania architektury i funkcjonowania membranowego urządzenia do przetwarzania wielu zestawów jest praktycznie nieskończony. Rzeczywiście, literatura dotycząca obliczeń membranowych zawiera bardzo dużą liczbę modeli. Tak więc MC nie jest jedynie teorią związaną z konkretnym modelem, jest ramą do opracowywania modeli podzielonych na przedziały.
Chemikalia są modelowane za pomocą symboli lub alternatywnie ciągów symboli. Region, który jest zdefiniowany przez membranę, może zawierać inne symbole lub ciągi (łącznie określane jako obiekty) lub inne membrany, tak że system P ma dokładnie jedną zewnętrzną membranę, zwaną membraną skórną, oraz hierarchiczną relację rządzącą wszystkimi jej membrany pod błoną skórną.
Jeśli przedmioty są symbolami, to ich wielość w obrębie regionu ma znaczenie; jednak multi-sets są również używane w niektórych modelach strunowych. Regiony mają powiązane reguły, które określają, w jaki sposób obiekty są produkowane, konsumowane, przekazywane do innych regionów i w inny sposób wchodzą ze sobą w interakcje. Niedeterministyczne, maksymalnie równoległe stosowanie reguł w całym systemie jest przejściem między stanami systemu, a sekwencja przejść nazywana jest obliczeniem. Poszczególne cele można zdefiniować tak, aby oznaczały stan zatrzymania, w którym to momencie wynikiem obliczeń byłyby obiekty zawarte w określonym regionie. Alternatywnie wynik może składać się z obiektów wysyłanych z błony skórnej do środowiska.
Zbadano wiele wariantów modeli, a zainteresowanie skupiło się na udowodnieniu uniwersalności obliczeniowej dla systemów z niewielką liczbą membran w celu rozwiązania problemów NP-zupełnych, takich jak problemy spełnialności Boole'a (SAT) i problem komiwojażera (TSP) . Systemy P mogą handlować złożonością przestrzenną i czasową i rzadziej wykorzystują modele do wyjaśniania naturalnych procesów zachodzących w żywych komórkach. W ramach badań opracowywane są modele, które przynajmniej teoretycznie można zaimplementować na sprzęcie. Do tej pory systemy P to prawie wszystkie modele teoretyczne, które nigdy nie zostały sprowadzone do praktyki, chociaż podano system praktyczny.