Optymalne dopełnienie szyfrowania asymetrycznego

W kryptografii Optimal Asymmetric Encryption Padding ( OAEP ) jest schematem uzupełniania często używanym razem z szyfrowaniem RSA . OAEP został wprowadzony przez Bellare i Rogaway , a następnie ustandaryzowany w PKCS#1 v2 i RFC 2437.

Algorytm OAEP jest formą sieci Feistela , która wykorzystuje parę losowych wyroczni G i H do przetwarzania tekstu jawnego przed szyfrowaniem asymetrycznym . W połączeniu z dowolną jednokierunkową permutacją z zapadnią , przetwarzanie to zostało udowodnione w losowym modelu wyroczni, dając połączony schemat, który jest semantycznie bezpieczny w przypadku $ataku$ z wybranym tekstem jawnym (IND-CPA) fa {\ displaystyle f . Udowodniono, że OAEP zaimplementowany z pewnymi permutacjami zapadni (np. RSA) jest również bezpieczny przed atakiem wybranym tekstem zaszyfrowanym . OAEP można wykorzystać do zbudowania transformacji typu „wszystko albo nic” .

OAEP spełnia następujące dwa cele:

Dodaj element losowości, który może być użyty do przekształcenia deterministycznego schematu szyfrowania (np. tradycyjnego RSA ) w schemat probabilistyczny .
Zapobiegaj częściowemu odszyfrowaniu tekstu zaszyfrowanego (lub wyciekowi innych informacji), upewniając się, że przeciwnik nie może odzyskać żadnej części tekstu jawnego bez możliwości odwrócenia jednokierunkowej $permutacji$ .

Oryginalna wersja OAEP (Bellare/Rogaway, 1994) wykazywała formę „ świadomości tekstu jawnego ” (co, jak twierdzili, implikuje zabezpieczenie przed atakiem wybranego tekstu zaszyfrowanego ) w modelu losowej wyroczni, gdy OAEP jest używany z dowolną permutacją zapadni. Późniejsze wyniki zaprzeczyły temu twierdzeniu, pokazując, że OAEP był bezpieczny tylko dla IND-CCA1 . Jednak oryginalny schemat został udowodniony w losowym modelu wyroczni jako IND-CCA2 bezpieczne, gdy używany jest OAEP z permutacją RSA przy użyciu standardowych wykładników szyfrowania, jak w przypadku RSA-OAEP. Aby rozwiązać ten problem, Victor Shoup zaoferował ulepszony schemat (nazwany OAEP +), który działa z dowolną jednokierunkową permutacją zapadni . Nowsze prace wykazały, że w modelu standardowym (to znaczy, gdy funkcje skrótu nie są modelowane jako losowe wyrocznie) niemożliwe jest udowodnienie bezpieczeństwa IND-CCA2 RSA-OAEP przy założonej twardości problemu RSA .

Algorytm

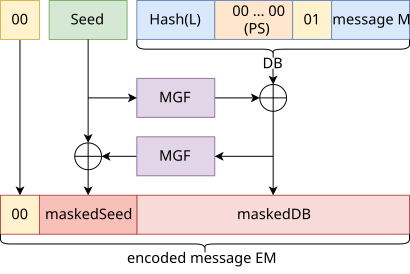
Schemat kodowania OAEP zgodnie z RFC 8017

na schemacie

MGF to funkcja generująca maskę , zwykle MGF1,
Hash to wybrana funkcja haszująca ,
hLen to długość wyjścia funkcji skrótu w bajtach,
k to długość modułu RSA n w bajtach,
M to wiadomość do dopełnienia (co najwyżej ${\ Displaystyle k-2 \ cdot \ operatorname {hLen} -2}$ bajtów),
L to opcjonalna etykieta, która ma być powiązana z wiadomością (domyślnie etykieta jest pustym ciągiem i może być używana do uwierzytelniania danych bez konieczności szyfrowania),
PS to ciąg bajtów składający się z ${\ Displaystyle k- \ operatorname {mLen} -2 \ cdot \ operatorname {hLen} -2}$ null-bajtów.
⊕ jest operacją XOR .

Kodowanie

RFC 8017 dla PKCS#1 v2.2 określa następujący schemat kodowania OAEP:

Zaszyfruj etykietę L za pomocą wybranej funkcji skrótu: ${\ Displaystyle \ operatorname {lHash} =\ operatorname {Hash} (L)}$
Wygeneruj ciąg dopełnienia PS składający się z bajtów o wartości 0x00 $\ Displaystyle k- \ operatorname {mLen} -2 \ cdot \ operatorname {hLen} -2} .$
Połącz lHash , PS , pojedynczy bajt 0x01 ${\ Displaystyle \ operatorname {DB} = \ operatorname {lHash} ||\ operatorname {PS} ||\ operatorname {0x01} ||\ operatorname {M}}$ wiadomość M w celu utworzenia bloku danych DB : . Ten blok danych ma długość ${\ Displaystyle k - \ operatorname {hLen} -1}$ bajtów.
Wygeneruj losowe ziarno o długości hLen .
Użyj funkcji generowania maski, aby wygenerować maskę o odpowiedniej długości dla bloku danych: $\ Displaystyle \ operatorname {dbMask } =\mathrm {MGF} (\mathrm {ziarno} ,k-\mathrm {hLen} -1)}$
Zamaskuj blok danych wygenerowaną maską: $Displaystyle \ operatorname {maskedDB} = \ operatorname {DB} \ oplus \ operatorname {dbMask}}$
Użyj funkcji generującej maskę, aby wygenerować maskę o długości hLen dla materiału siewnego: $Displaystyle \ operatorname {seedMask } =\mathrm {MGF} (\mathrm {maskedDB} ,\mathrm {hLen} )}$
Zamaskuj ziarno wygenerowaną maską: $operatorname {ziarno} \ oplus \ operatorname {SeedMask} }$
Zakodowana (dopełniona) wiadomość to bajt 0x00 połączony z maskedSeed i maskedDB : ${\ Displaystyle \ operatorname {EM} = \ operatorname {0x00} ||\ operatorname {maskedSeed} ||\ operatorname {maskedDB}$

Rozszyfrowanie

Dekodowanie polega na odwróceniu kroków wykonanych w algorytmie kodowania:

Zaszyfruj etykietę L za pomocą wybranej funkcji skrótu: ${\ Displaystyle \ operatorname {lHash} =\ operatorname {Hash} (L)}$
Aby odwrócić krok 9, podziel zakodowaną wiadomość EM na bajt 0x00, maskedSeed (o długości hLen ) i maskedDB : ${\ Displaystyle \ operatorname {EM} = \ operatorname {0x00} ||\ operatorname {maskedSeed} ||\ operatorname {maskedDB}$
s mi ${seedMask$ re za = sol
$\ Displaystyle \ operatorname {ziarno} = \ operatorname {maskedSeed} \oplus \mathrm {seedMask} }$ odwrócić krok 8, odzyskaj ziarno za pomocą seedMask :
Wygeneruj dbMask , który został użyty do zamaskowania bloku danych: $\ Displaystyle \ operatorname {dbMask} = \ operatorname {MGF } (\mathrm {ziarno} ,k-\mathrm {hLen} -1)}$
$_ }$ blok DB
Aby odwrócić krok 3, podziel blok danych na części: ${\ Displaystyle \ operatorname {DB} = \ operatorname {lHash'} ||\ operatorname {PS} ||\ operatorname {0x01} ||\ operatorname {M}}$ $\mathrm {DB} =\mathrm {lHash'} ||\mathrm {PS} ||\mathrm {0x01} ||\mathrm {M}$ .
1. Zweryfikuj to:
  - lHash' jest równy obliczonemu lHash
  - PS składa się tylko z bajtów 0x00
  - PS i M są oddzielone bajtem 0x01 i
  - pierwszy bajt EM to bajt 0x00.
2. Jeśli którykolwiek z tych warunków nie jest spełniony, dopełnienie jest nieprawidłowe.

Użycie w RSA: Zaszyfrowaną wiadomość można następnie zaszyfrować za pomocą RSA. Deterministycznej właściwości RSA można teraz uniknąć, stosując kodowanie OAEP, ponieważ ziarno jest generowane losowo i wpływa na całą zakodowaną wiadomość.

Bezpieczeństwo

„ wszystko albo nic ” wynika z faktu, że aby odzyskać M , należy odzyskać cały maskedDB i cały maskedSeed ; maskedDB jest wymagany do odzyskania materiału siewnego z maskedSeed , a materiał siewny jest wymagany do odzyskania DB bloku danych z maskedDB . Ponieważ każdy zmieniony bit kryptograficznego skrótu całkowicie zmienia wynik, cały maskedDB i cały maskedSeed oba muszą być całkowicie wyleczone.

Realizacja

W standardzie PKCS#1 losowe wyrocznie są identyczne. Standard PKCS#1 wymaga ponadto, aby losowe wyrocznie były MGF1 z odpowiednią funkcją skrótu.

Zobacz też

Enkapsulacja klucza

^ M. Bellare , P. Rogaway . Optymalne szyfrowanie asymetryczne — Jak szyfrować za pomocą RSA . Rozszerzone streszczenie w Advances in Cryptology - Eurocrypt '94 Proceedings, Lecture Notes in Computer Science Cz. 950, red. A. De Santis, Springer-Verlag , 1995. pełna wersja (pdf)
^ Eiichiro Fujisaki, Tatsuaki Okamoto, David Pointcheval i Jacques Stern . RSA — OAEP jest bezpieczny przy założeniu RSA . W J. Kilian, red., Advances in Cryptology - CRYPTO 2001, tom. 2139 notatek z wykładów z informatyki, SpringerVerlag, 2001. pełna wersja (pdf)
Bibliografia _ OAEP ponowne rozpatrzenie . IBM Zurich Research Lab, Saumerstr. 4, 8803 Ruschlikon, Szwajcaria. 18 września 2001. pełna wersja (pdf)
^ P. Paillier i J. Villar, Handel jednokierunkowy przeciwko bezpieczeństwu wybranego szyfrogramu w szyfrowaniu opartym na faktoringu , Postępy w kryptologii - Asiacrypt 2006.
^ D. Brown, Jakie skróty zapewniają bezpieczeństwo RSA-OAEP? , IACR ePrint 2006/233.
^ „Operacja szyfrowania” . PKCS #1: Specyfikacje kryptograficzne RSA Wersja 2.2 . IETF . listopad 2016 r. s. 22. sek. 7.1.1. doi : 10.17487/RFC8017 . RFC8017 . _ Źródło 2022-06-04 .
^ Brązowy, Daniel RL (2006). „Jakie skróty zapewniają bezpieczeństwo RSA-OAEP?” (PDF) . IACR Cryptology ePrint Archiwum . Źródło 2019-04-03 .

[1] M. Bellare , P. Rogaway . Optymalne szyfrowanie asymetryczne — Jak szyfrować za pomocą RSA . Rozszerzone streszczenie w Advances in Cryptology - Eurocrypt '94 Proceedings, Lecture Notes in Computer Science Cz. 950, red. A. De Santis, Springer-Verlag , 1995. pełna wersja (pdf)

[2] Eiichiro Fujisaki, Tatsuaki Okamoto, David Pointcheval i Jacques Stern . RSA — OAEP jest bezpieczny przy założeniu RSA . W J. Kilian, red., Advances in Cryptology - CRYPTO 2001, tom. 2139 notatek z wykładów z informatyki, SpringerVerlag, 2001. pełna wersja (pdf)

[3] Bibliografia _ OAEP ponowne rozpatrzenie . IBM Zurich Research Lab, Saumerstr. 4, 8803 Ruschlikon, Szwajcaria. 18 września 2001. pełna wersja (pdf)

[4] P. Paillier i J. Villar, Handel jednokierunkowy przeciwko bezpieczeństwu wybranego szyfrogramu w szyfrowaniu opartym na faktoringu , Postępy w kryptologii - Asiacrypt 2006.

[5] D. Brown, Jakie skróty zapewniają bezpieczeństwo RSA-OAEP? , IACR ePrint 2006/233.

[6] „Operacja szyfrowania” . PKCS #1: Specyfikacje kryptograficzne RSA Wersja 2.2 . IETF . listopad 2016 r. s. 22. sek. 7.1.1. doi : 10.17487/RFC8017 . RFC8017 . _ Źródło 2022-06-04 .

[7] Brązowy, Daniel RL (2006). „Jakie skróty zapewniają bezpieczeństwo RSA-OAEP?” (PDF) . IACR Cryptology ePrint Archiwum . Źródło 2019-04-03 .