Problem z pakowaniem pasków

Problem upakowania pasków jest dwuwymiarowym problemem minimalizacji geometrycznej. Mając zestaw ustawionych w jednej osi prostokątów oraz pasek o ograniczonej szerokości i nieskończonej wysokości, określ upakowanie prostokątów w pasku bez nakładania się, minimalizując jego wysokość. Ten problem jest problemem cięcia i pakowania i jest klasyfikowany jako problem otwartego wymiaru według Wäschera i in.

Problem ten pojawia się w obszarze planowania, gdzie modeluje zadania, które wymagają ciągłej części pamięci w danym okresie. Innym przykładem jest dziedzina produkcji przemysłowej, gdzie prostokątne kawałki muszą być wycinane z arkusza materiału (np. tkaniny lub papieru) o stałej szerokości, ale nieskończonej długości, i chce się zminimalizować straty materiału.

Problem ten został po raz pierwszy zbadany w 1980 roku. Jest silnie NP trudny i nie istnieje algorytm aproksymacji czasu wielomianowego o współczynniku mniejszym niż ${\ displaystyle 3/2}$ , chyba że ${\ displaystyle P = NP}$ . Jednak najlepszy dotychczas osiągnięty współczynnik aproksymacji (za pomocą algorytmu czasu wielomianowego Harrena i wsp $,$ istnieje algorytm ze współczynnikiem aproksymacji ${\ Displaystyle 3/2}$ .

Definicja

Instancja problemu $_$ pasków składa $.$ _ , a także zestaw $elementów$ . Każdy element $in {\ mathcal {I}}}$ szerokość ${\ Displaystyle w_ {i} \ in (0,1] \ cap \ mathbb {Q}}$ i wysokość ${\ Displaystyle h_ {i} \ in (0,1] \ cap \ mathbb {Q} }$ Pakowanie elementów to mapowanie, które odwzorowuje każdy lewy dolny róg elementu na pozycję ${\ displaystyle i \ in {\ mathcal {I}}}$${\ Displaystyle (x_ {i}, y_ {i}) \ in ([0,1-w_ {i}] \ czapka \ mathbb {Q}) \ razy \ mathbb {Q} _ { \geq 0}}$ wewnątrz paska. Wewnętrzny punkt umieszczonego $zbioru$ punktem ${\ Displaystyle \ operatorname {zajazd} (i) = \ {(x, y) \ w \ mathbb {Q} \ razy \ mathbb {Q} | x_ {i}<x<x_{i}+w_{i},y_{i}<y<y_{i}+h_{i}\}}$ . Dwa (umieszczone) elementy nakładają się na siebie, jeśli mają wspólny punkt wewnętrzny. Wysokość wypełnienia określa się jako ${\ Displaystyle \ max \ {y_ {i} + h_ {i} | ja \ w {\ mathcal {I}} \}}$ . Celem jest znalezienie wolnego od zachodzenia na siebie upakowania przedmiotów wewnątrz paska przy jednoczesnym zminimalizowaniu wysokości upakowania.

Ta definicja jest używana dla wszystkich algorytmów czasu wielomianowego. Dla czasu pseudowielomianowego i algorytmów FPT definicja została nieznacznie zmieniona w celu uproszczenia zapisu. W tym przypadku wszystkie pojawiające się rozmiary są integralne. Zwłaszcza szerokość paska jest określona przez dowolną liczbę całkowitą większą niż 1. Należy zauważyć, że te dwie definicje są równoważne.

Warianty

Istnieje kilka wariantów problemu upakowania pasków, które zostały zbadane. Warianty te dotyczą geometrii przedmiotów, wymiarów problemu, możliwości obracania przedmiotów oraz konstrukcji opakowania.

Geometria przedmiotów: W standardowym wariancie tego zadania zbiór danych przedmiotów składa się z prostokątów. W często rozważanym podprzypadku wszystkie elementy muszą być kwadratami. Wariant ten był już rozważany w pierwszej pracy dotyczącej pakowania taśmowego. Dodatkowo zbadano warianty, w których kształty są okrągłe lub nawet nieregularne. W tym drugim przypadku mówimy o nieregularnym upakowaniu taśmowym .

Wymiar: Jeśli nie wspomniano inaczej, problem pakowania pasków jest problemem dwuwymiarowym. Jednak badano go również w trzech lub nawet więcej wymiarach. W tym przypadku obiekty są hiperprostokątami , a pasek jest otwarty w jednym wymiarze i ograniczony w pozostałych.

Rotacja: W klasycznym problemie pakowania w paski nie wolno obracać przedmiotów. Jednak zbadano warianty, w których dozwolony jest obrót o 90 stopni lub nawet dowolny kąt.

Struktura wypełnienia: W ogólnym problemie pakowania taśmowego struktura wypełnienia nie ma znaczenia. Istnieją jednak aplikacje, które mają wyraźne wymagania dotyczące struktury opakowania. Jednym z tych wymagań jest możliwość wycinania elementów z paska przez poziome lub pionowe cięcie od krawędzi do krawędzi. Szczeliwa umożliwiające tego rodzaju cięcie nazywane są szczeliwami gilotynowymi .

Twardość

Problem pakowania pasków zawiera problem pakowania bin jako szczególny przypadek, gdy wszystkie przedmioty mają tę samą wysokość 1. Z tego powodu jest on silnie NP-trudny i nie może istnieć algorytm aproksymacji czasu wielomianowego , który ma współczynnik aproksymacji mniejszy niż ${\ Displaystyle 3/2}$ chyba że ${\ Displaystyle P = NP}$ . Ponadto, chyba że nie może istnieć czas pseudowielomianowy ${\ displaystyle P = NP}$ $z$ mniejszy niż co można udowodnić przez redukcję z silnie NP-zupełnego problemu 3 partycjami . Zauważ, że obie dolne granice i $5/4} obowiązują również w przypadku$$displaystyle$ gdy obrót elementów o 90 stopni jest Dodatkowo udowodnili to Ashok i in. że wypełnienie paskowe jest W[1]-twarde przy parametryzacji wysokością optymalnego upakowania.

Własności rozwiązań optymalnych

Istnieją dwie trywialne dolne granice optymalnych rozwiązań. Pierwsza to wysokość największego przedmiotu. Zdefiniuj ${\ Displaystyle h _ {\ max} (ja): = \ max \ {h (i) | i \ in {\ mathcal {I}} \}}$ . Wtedy to trzyma

${\ Displaystyle OPT (ja) \ geq h _ {\ max} (ja)}$ .

Kolejna dolna granica jest określona przez całkowitą powierzchnię przedmiotów. ZA ${\ Displaystyle \ operatorname {OBSZAR} ({\ mathcal {I}}): = \ suma _ {i \ w {$ to to trzyma

${\ Displaystyle OPT (I) \ geq \ operatorname {OBSZAR} ({\ mathcal {I}}) / W}$ .

Poniższe dwie dolne granice uwzględniają fakt, że pewnych elementów nie można umieścić obok siebie w pasku i można je obliczyć w ${\ Displaystyle {\ mathcal {O}} (n \log(n))}$ . Dla pierwszej dolnej granicy załóżmy, że elementy są posortowane według nierosnącej wysokości. Zdefiniuj ${\ Displaystyle k: = \ max \ {i: \ suma _ {j = 1} ^ {k} w (j) \ równoważnik W \}}$ . l ${\ Displaystyle l> k}$ zdefiniuj pierwszy indeks taki, że $\ Displaystyle i (l) \ równoważnik}$${\ Displaystyle w (l) + \ suma _ {j = 1} ^ {i (l)} w (j)> W}$ . Wtedy to trzyma

${\ Displaystyle OPT (I) \ geq \ max \ {h (l) + h (i (l)} | l> k \ klin w (l) + \ suma _ {j = 1} ^ {i (l) }w(j)>W\}}$ .

W przypadku drugiej dolnej granicy podziel zestaw elementów na trzy zestawy. Niech ${\ Displaystyle \ alfa \ w [1, W / 2] \ cap \ mathbb {N}}$ i zdefiniuj ${\ Displaystyle {\ mathcal {I}} _ {1} (\ alfa): = \ {i \ in {\ mathcal {I}} | w (i)> W- \ alfa \}}$ , ${\ Displaystyle {\ mathcal {I}} _ {2} (\ alfa): = \ {i \ w {\ mathcal {I}} | W- \ alfa \geq w(i)>W/2\}}$ , a ${\ Displaystyle {\ mathcal {I}} _ {3} (\ alfa): = \ {i \ in {\ mathcal {I}} | W / 2 \ geq w (i)> \ alfa \} }$ . Wtedy to trzyma

${\ Displaystyle OPT (I) \ geq \ max _ {\ alfa \ w [1, W / 2]\cap \mathbb {N}}{\Bigg \{}\sum _{i\in {\mathcal {I}}_{1}(\alpha )\cup {\mathcal {I}}_{2 }(\alpha)}h(i)+\left({\frac {\sum _{i\in {\mathcal {I}}_{3}(\alpha)h(i)w(i)-\ suma _{i\in {\mathcal {I}}_{2}(\alpha)}(Ww(i))h(i)}}{W}}\right)_{+}{\Bigg \} }}$ , gdzie ${\ Displaystyle (x) _ {+}: = \ max \ {x, 0 \}}$ dla każdego ${\ Displaystyle x \ w \ mathbb {R}}$ .

Z drugiej strony Steinberg wykazał, że górna granica wysokości rozwiązania optymalnego może być ograniczona przez

${\ Displaystyle OPT (ja) \ równoważnik 2 \ max \ {h _ {\ max} (ja), \ operatorname {OBSZAR} ({\ mathcal {I}}) / W \}.}$

Dokładniej pokazał, że za ${\ Displaystyle W \ geq w _ {\ max} ({\ mathcal {I}})}$ i za ${\ Displaystyle H \ geq h _ {\ max} (I)},$${\ displaystyle {\ displaystyle$ elementy można umieścić w pudełku o szerokości $,$ wysokości jeśli ja $}$

$WH \ geq 2 \ operatorname {OBSZAR} ({\ mathcal {I}})+(2w_{\max }({\mathcal {I}})-W)_{+}(2h_{\max }(I)-H)_{+}} ,$ gdzie ${\ Displaystyle (x) _ {+}: = \ max \ {x, 0 \}}$ .

Algorytmy aproksymacji czasu wielomianowego

Ponieważ ten problem jest NP-trudny, zbadano algorytmy aproksymacji dla tego problemu. Większość podejść heurystycznych ma współczynnik aproksymacji między ${\ displaystyle 3}$ a ${\ displaystyle 2}$ . Znalezienie algorytmu o współczynniku poniżej $wydaje$ trudne, a złożoność odpowiednich algorytmów wzrasta, jeśli chodzi o ich czas działania i opisy. Najmniejszy osiągnięty dotychczas współczynnik aproksymacji to ${\ Displaystyle (5/3+ \ varepsilon)}$ .

Przegląd przybliżeń czasu wielomianowego

Rok	Nazwa	Gwarancja zbliżenia	Źródło
1980	Od dołu do góry z wyrównaniem do lewej (BL)	${\ Displaystyle 3OPT (ja)}$	Baker i in.
1980	Next-Fit Malejąca wysokość (NFDH)	${\ Displaystyle 2OPT (I) + h _ {\ max} (ja) \ równoważnik 3OPT (ja)}$	Coffmana i in.
	Malejąca wysokość pierwszego dopasowania (FFDH)	${\ Displaystyle 1.7OPT (I) + h _ {\ max} (ja) \ równoważnik 2,7OPT (I)}$
	Rozcięcie (SF)	${\ Displaystyle 1.5OPT (ja) + 2h _ {\ max} (ja)}$
1980		${\ Displaystyle 2OPT (I) + h _ {\ max} (ja) / 2 \ równoważnik 2,5OPT (ja)}$	Sleator
1981	Algorytm dzielony (SP)	${\ Displaystyle 3OPT (ja)}$	Golan
	Algorytm mieszany	${\ Displaystyle (4/3) OP (I) + 7 {\ Frac {1} {18}} h _ {\ max} ( I)}$
1981	góra-dół (UD)	${\ Displaystyle (5/4) OP (I) + 6 {\ Frac {7} {8}} h _ {\ max} ( I)}$	Baker i in.
1994	Dopasowanie odwrotne	${\ Displaystyle 2OPT (ja)}$	Schiermeyera
1997		${\ Displaystyle 2OPT (ja)}$	Steinberga
2000		${\ Displaystyle (1 + \ varepsilon) OPT (ja) + {\ mathcal {O}} (1 / \ varepsilon ^{2})h_{\max}(I)}$	Kenyon, Remila
2009		${\ Displaystyle 1.9396OPT (I)}$	Harren, van Stee
2009		${\ Displaystyle (1 + \ varepsilon) OPT (ja) + h _ {\ max} (ja)}$	Jansen, Solis-Oba
2011		${\ Displaystyle (1 + \ varepsilon) OPT (ja) + {\ mathcal {O}} (\log(1/\varepsilon )/\varepsilon )h_{\max }(I)}$	Bougereta i in.
2012		${\ Displaystyle (1 + \ varepsilon) OPT (ja) + {\ mathcal {O}} (\log(1/\varepsilon )/\varepsilon )h_{\max }(I)}$	Świrydenko
2014		${\ Displaystyle (5/3 + \ varepsilon) OPCJA (ja)}$	Harren i in.

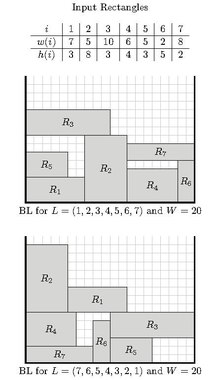
Od dołu do góry z wyrównaniem do lewej (BL)

Przykład rozwiązań wygenerowanych przez algorytm Bottom-Up Left-Justified.

Algorytm ten został po raz pierwszy opisany przez Bakera i in. Działa to w następujący sposób:

Niech $.$ ciągiem elementów prostokątnych Algorytm iteruje sekwencję w podanej kolejności. Dla każdego $w$ elementu szuka najniższej pozycji, aby go umieścić, a następnie przesuwa go jak najdalej W związku z tym umieszcza się na najniższej najbardziej lewej współrzędnej ${\ Displaystyle (x, y)}$$pasku$ .

Ten algorytm ma następujące właściwości:

• Współczynnik aproksymacji tego algorytmu nie może być ograniczony stałą. Dokładniej pokazali, że dla każdego ${ \ Displaystyle BL (L) / OPT (L)> M}$$elementów$ prostokątnych $uporządkowanych$ według rosnącej szerokości tak, , gdzie ${\ Displaystyle BL (L)}$$displaystyle$ jest wysokość upakowania utworzonego przez algorytm BL i optymalnego dla $L$ }
• Jeśli elementy są uporządkowane według malejących szerokości, to ${\ Displaystyle BL (L) / OPT (L) \ równoważnik 3}$ .
• Jeśli wszystkie elementy są kwadratami i są uporządkowane według malejących szerokości, to ${\ Displaystyle BL (L) / OPT (L) \ równoważnik 2}$ .
• Dla każdego $,$$\ Displaystyle BL(L)/OPC(L)>3-\delta }$ prostokątów $uporządkowanych według malejących szerokości$ tak że . .
• Dla każdego $uporządkowanych$$\ Displaystyle BL(L)/OPC(L)>2-\delta }$ kwadratów $według$ malejących szerokości, tak że . .
• ${\ Displaystyle BL (L) / OPT (L)> {\ Frac {12} {11 + \ varepsilon}}} ,$ każdego ${\ Displaystyle \ varepsilon \ in (0,1]}$ istnieje instancja zawierająca tylko kwadraty, w których każdy rząd kwadratów $ma$ stosunek tj. istnieją przypadki, w których BL nie znaleźć optimum nawet przy iteracji wszystkich możliwych rzędów pozycji.

Malejąca wysokość następnego dopasowania (NFDH)

Przykład NFDH i FFDH zastosowany do tej samej instancji

Algorytm ten został po raz pierwszy opisany przez Coffmana i in. w 1980 roku i działa w następujący sposób:

Niech będzie $.$ zestawem prostokątnych elementów Najpierw algorytm sortuje elementy według nierosnącej wysokości. Następnie, zaczynając od pozycji $,$ algorytm umieszcza elementy obok siebie na pasku, aż następny element nałoży się na prawą W tym momencie algorytm definiuje nowy poziom na górze najwyższego elementu na bieżącym poziomie i umieszcza elementy obok siebie na tym nowym poziomie.

Ten algorytm ma następujące właściwości:

• Czas działania może być ograniczony przez ${\ Displaystyle {\ mathcal {O}} (| {\ mathcal {I}} |\ log (| {\ mathcal {I} }|))}$ i jeśli elementy są już posortowane nawet według ${\ Displaystyle {\ mathcal {O}} (| {\ mathcal {I}} |)}$ .
• ${\ Displaystyle NFDH ({\ mathcal {I}}) \ równoważnik 2OPT ({\ mathcal {I}}) + h _ {\ max} \ równoważnik 3OPT ({\ mathcal {I}})}, gdzie$ każdego zestawu elementów tworzy opakowanie o $ja$ h $\ styl wyświetlania h_ {\ max }}$ jest największą wysokością elementu w $displaystyle {\ mathcal {I}}}$ \
• Dla $,$${\ Displaystyle NFDH ({\ mathcal {I}} |)> (2- \ varepsilon) OPT ({\ mathcal {I}}).}$ zbiór taki $ja$
• Wygenerowane opakowanie jest opakowaniem gilotynowym. Oznacza to, że przedmioty można uzyskać poprzez sekwencję poziomych lub pionowych cięć od krawędzi do krawędzi.

Malejąca wysokość pierwszego dopasowania (FFDH)

Algorytm ten, po raz pierwszy opisany przez Coffmana i in. w 1980 roku działa podobnie do algorytmu NFDH. Jednak podczas umieszczania kolejnego elementu algorytm skanuje poziomy od dołu do góry i umieszcza przedmiot na pierwszym poziomie, na którym się zmieści. Nowy poziom jest otwierany tylko wtedy, gdy przedmiot nie pasuje do żadnego poprzedniego.

Ten algorytm ma następujące właściwości:

• Czas działania może być ograniczony przez ${\ Displaystyle {\ mathcal {O}} (| {\ mathcal {I}} | ^ {2}$ ) ${\ Displaystyle | {\ mathcal {I}} |}$ poziomów.
• ${ \ Displaystyle FFDH ({\ mathcal {I}}) \ równoważnik 1,7OPT ({\ mathcal {I}}) + h _ {\ max} \ równoważnik 2,7OPT ({\ mathcal {I}})},$ każdego zestawu elementów tworzy opakowanie o $ja$ gdzie ${ \ displaystyle h _ {\ maks.}}$ jest największą wysokością elementu w $displaystyle {\ mathcal {I}}}$ \
• Niech ${\ displaystyle m \ geq 2}$ . Dla $i$ zestawu elementów paska o szerokości takiej, że $/ m}$$Displaystyle w (i) \ równoważnik$ dla każdego $ja$ że ${\ Displaystyle FFDH ({\ mathcal {I}}) \ równoważnik \ lewo (1 + 1 / m \ prawo) OPT ({\ mathcal {I}}) +h_{\max}}$ . Ponadto dla każdego istnieje taki zestaw elementów z $\ Displaystyle \ varepsilon > 0} ,$ z którym $)$${\ Displaystyle FFDH ({\ mathcal {I}})> \ lewo (1 + 1 / m- \ varepsilon \ prawej) OPT ({\ mathcal {I}})}$ .
• Jeśli wszystkie elementy w $)$ kwadratami, oznacza to, że $\ Displaystyle FFDH ( {\mathcal {I}})\leq (3/2)OPT({\mathcal {I}})+h_{\max}}$ . Ponadto dla każdego istnieje zbiór kwadratów I $\ displaystyle \ varepsilon > 0}$${\ Displaystyle {\ mathcal {I}}}$ takie, że $FFDH ({\ mathcal {I}})> \ lewo (3/2-\varepsilon \right)OPT({\mathcal {I}})}$ .
• Wygenerowane opakowanie jest opakowaniem gilotynowym. Oznacza to, że przedmioty można uzyskać poprzez sekwencję poziomych lub pionowych cięć od krawędzi do krawędzi.

Algorytm dzielonego dopasowania (SF)

Algorytm ten został po raz pierwszy opisany przez Coffmana i in. Dla danego zestawu elementów i paska o szerokości $\$ to w następujący sposób: $mathcal {I}}}$

1. Wyznacz $całkowitą taką$$mniejszą$ że dane prostokąty szerokość
2. ja ${\ Displaystyle {\ mathcal {I}}}$ na dwa zestawy $\ Displaystyle {\ mathcal {I}} _ {szeroki}}$ i ${\ displaystyle {\ mathcal {I}} _ {wąski}}$ tak, że ${\ Displaystyle {\ mathcal {I}} _ {szeroki}}$ zawiera wszystkie elementy ${\ displaystyle i \ in {\ mathcal {ja }}}$ o szerokości ${\ Displaystyle w (i)> W / (m + 1)}$ podczas gdy ${\ Displaystyle {\ mathcal {I}} _ {wąski}}$ zawiera wszystko elementy z ${\ Displaystyle w (i) \ równoważnik W / (m + 1)}$ .
3. Zamów ${\ Displaystyle {\ mathcal {I}} _ {szeroki}}$ i ${\ Displaystyle {\ mathcal {I}} _ {wąski}}$ według nierosnącej wysokości.
4. $_$ elementy .
5. Zmień kolejność poziomów / półek skonstruowanych przez FFDH tak, aby wszystkie półki o całkowitej szerokości większej niż znajdowały się poniżej ${\ Displaystyle W (m + 1) / (m + 2)}$ węższe.
6. $bardziej$$prostokątny$ obszar obok wąskich poziomów / półek,
7. $aby$$,$ elementy również obszaru

Ten algorytm ma następujące właściwości:

• ${\ Displaystyle SF ({\ mathcal {I}}) \ równoważnik (m + 2) / (m + 1) OPT ({\ mathcal {I}}) + 2h _ {\ max}}$ zestawu odpowiadającego im $)$$ja$ . Zauważ, że dla ${\ Displaystyle m = 1}$ , utrzymuje, że ${\ Displaystyle SF ({\ mathcal {I}}) \ równoważnik (3 /2)OPT({\mathcal {I}})+2h_{\max }}$
• Dla każdego ${\ Displaystyle \ varepsilon > 0}$$istnieje$ zestaw elementów takich, ${\ Displaystyle SF ({\ mathcal {I}})> \ lewo ((m + 2) / (m + 1) - \ varepsilon \ prawej) OPT ({\ mathcal { ja}})}$ .

Algorytm Sleatora

Dla danego zestawu elementów i paska o szerokości $\$ to w następujący sposób: $mathcal {I}}}$

1. Znajdź wszystkie elementy o szerokości większej niż $ułóż je na$ paska (w losowej kolejności) Nazwij całkowitą wysokość tych elementów ${\ displaystyle h_ {0}}$ . Wszystkie pozostałe elementy zostaną umieszczone powyżej ${\ displaystyle h_ {0}}$ .
2. Posortuj wszystkie pozostałe elementy w nierosnącej kolejności wysokości. Elementy zostaną umieszczone w tej kolejności.
3. $Rozważ$ poziomą linię na . Algorytm umieszcza przedmioty na tej półce w nierosnącej kolejności wysokości, aż nie pozostanie żaden przedmiot lub następny się nie zmieści.
4. Narysuj pionową linię w $, która$ pasek na dwie równe połowy
5. Niech $będzie najwyższym$$odpowiednim punktem$ objętym dowolnym elementem w lewej połowie i prawej Narysuj dwa poziome odcinki linii o długości ${\ Displaystyle W/2}$ w ${\ displaystyle h_ {l}}$ i ${\ displaystyle h_ {r}}$ wzdłuż lewej i prawej połowy paska. Te dwie linie budują nowe półki, na których algorytm umieści przedmioty, tak jak w kroku 3. Wybierz połowę, która ma dolną półkę i umieszczaj przedmioty na tej półce, aż żaden inny przedmiot się nie zmieści. Powtarzaj ten krok, aż nie pozostanie żaden element.

Ten algorytm ma następujące właściwości:

• Czas działania może być ograniczony przez ${\ Displaystyle {\ mathcal {O}} (| {\ mathcal {I}} |\ log (| {\ mathcal {I} }|))}$ i jeśli elementy są już posortowane nawet według ${\ Displaystyle {\ mathcal {O}} (| {\ mathcal {I}} |)}$ .
• ${$ każdego zestawu elementów tworzy opakowanie o wysokości $ja$ gdzie ${ \ displaystyle h _ {\ maks.}}$ jest największą wysokością elementu w $displaystyle {\ mathcal {I}}}$ \

Algorytm podziału (SP)

Algorytm ten jest rozszerzeniem podejścia Sleatora i został po raz pierwszy opisany przez Golana. Umieszcza elementy w nierosnącej kolejności szerokości. Intuicyjnym pomysłem jest podzielenie paska na podpaski podczas umieszczania niektórych elementów. $jest$ to możliwe, algorytm umieszcza bieżący element $.$ już umieszczonego W tym przypadku dzieli odpowiedni pasek podrzędny na dwie części: jedną zawierającą pierwszy element, $a$ zawierającą bieżący element ${\ displaystyle i}$ . Jeśli nie jest to możliwe, umieszcza się $.$ już umieszczonym elemencie i nie dzieli podpaska

Algorytm ten tworzy zestaw S pasków podrzędnych. Dla każdego podpaska s ∈ S znamy jego lewy dolny róg s.xposition i s.yposition , jego szerokość s.szerokość , poziome linie równoległe do górnej i dolnej granicy przedmiotu umieszczonego jako ostatni w tym podpasku s. upper i s.lower , a także jego szerokość s.itemWidth .

     
      funkcja  Split Algorithm (SP)  jest  wprowadzana:  elementy  I  , szerokość paska  W  dane wyjściowe:  Pakowanie elementów  Sortuj I w nierosnącym porządku szerokości; Zdefiniuj pustą listę S podpasków;  Zdefiniuj nowy podpasek s za pomocą s.xposition = 0, s.yposition = 0, s.width = W, s.lower = 0, s.upper = 0, s.itemWidth = W;  Dodaj s do S;   podczas gdy  ja nie opróżniam,  czy  i := I.pop();  Usuwa najszerszy przedmiot z 
        
             Definiuję nową listę S_2 zawierającą wszystkie podpaski o szerokości s - s.itemWidth ≥ i.width;  S_2 zawiera wszystkie podpaski, w których i mieści się obok już umieszczonego elementu,  jeśli  S_2 jest pusty ,   to  w takim przypadku umieść element na innym.  Znajdź podpasek s w S z najmniejszym s.upper;  tj. najmniej wypełniony podpasek  Umieść i w pozycji (s.xposition, s.upper); Aktualizuj s: s.lower := s.upper;  s.górna := s.górna+i.wysokość;  s.itemWidth := i.width;   w przeciwnym razie  
             W takim przypadku umieść przedmiot obok innego na tym samym poziomie i podziel odpowiedni podpasek w tym miejscu.  Znajdź s ∈ S_2 z najmniejszym s.lower; Umieść i na pozycji (s.xposition + s.itemWidth, s.lower);  Usuń s z S;  Zdefiniuj dwa nowe podpaski s1 i s2 za pomocą s1.xposition = s.xposition, s1.yposition = s.upper, s1.width = s.itemWidth, s1.lower = s.upper, s1.upper = s.upper, s1.itemWidth = s.itemWidth;  s2.xposition = s.xposition+s.itemWidth, s2.yposition = s.lower, s2.width = s.width - s.itemWidth, s2.lower = s.lower, s2.górny = s.lower + i. wysokość, s2.itemWidth = i.szerokość;  S.add(s1,s2);   Funkcja końca  powrotu  

Ten algorytm ma następujące właściwości:

• Czas działania może być ograniczony przez ${\ mathcal {I}} | ^ {2})},$ jest ograniczona ${\ Displaystyle | {\ mathcal {I}} |}$ .
• $ja$ zestawu elementów oznacza to, że $\ Displaystyle SP ({ \mathcal {I}})\leq 2OPT({\mathcal {I}})+h_{\max}\leq 3OPT({\mathcal {I}})}$ .
• Dla każdego ${\ Displaystyle \ varepsilon > 0}$${\ Displaystyle SP ({\ mathcal {I}})> (3- \ varepsilon) OPT ({\ mathcal {I}})}$$zbiór$ elementów takich, że .
• Dla $>$ i ${\ Displaystyle SP ({\ mathcal {I}})> (2- \ varepsilon) OPT ({\ mathcal {I}}) + C}$ zestaw $)$$,$ że .

Dopasowanie odwrotne (RF)

Algorytm ten został po raz pierwszy opisany przez Schiermeyera. Opis tego algorytmu wymaga dodatkowej notacji. Dla umieszczonego przedmiotu $Displaystyle$ dolny róg jest oznaczony przez $(a_ {i}, c_ {i}) }$ i jego prawy górny róg przez ${\ Displaystyle (b_ {i}, d_ {i})}$ .

Biorąc pod uwagę zestaw elementów i ${\ displaystyle$ szerokości , działa to w następujący sposób: ${\ mathcal {I}}}$

1. Ułóż wszystkie prostokąty o szerokości większej niż $na$ na dole paska. Oznacz przez ${\ displaystyle H_ {0}}$ wysokość tego stosu. Wszystkie inne elementy zostaną zapakowane powyżej ${\ displaystyle H_ {0}}$ .
2. Posortuj pozostałe elementy według nierosnącej wysokości i rozważ elementy w tej kolejności w kolejnych krokach. Niech ${\ displaystyle h _ {\ max}}$ będzie wysokością najwyższego z tych pozostałych elementów.
3. Umieść elementy jeden po drugim wyrównane do lewej na półce określonej przez ${\ displaystyle H_ {0}},$ aż żaden inny przedmiot nie zmieści się na tej półce lub nie zostanie żaden przedmiot. Nazwij tę półkę pierwszym poziomem .
4. Niech $.$ wysokością najwyższego rozpakowanego Zdefiniuj nową półkę w ${\ displaystyle H_ {0} + h_ {\ max} + h_ {1}}$ . Algorytm wypełni tę półkę od prawej do lewej, wyrównując przedmioty do prawej, tak aby dotykały tej półki górą. Nazwij tę półkę drugim odwróconym poziomem .
5. Umieść przedmioty na dwóch półkach dzięki pierwszemu dopasowaniu, tj. umieszczając przedmioty na pierwszym poziomie, gdzie pasują, a na drugim w przeciwnym razie. Kontynuuj, aż nie będzie żadnych przedmiotów lub całkowita szerokość przedmiotów na drugiej półce wyniesie co najmniej ${\ displaystyle W/2}$ .
6. Przesuń drugi odwrócony poziom w dół, aż przedmiot z niego dotknie przedmiotu z pierwszego poziomu. Zdefiniuj $pozycję$ przesuniętej półki. Niech i $.$ najbardziej po prawej parą stykających się elementów z $umieszczonymi$$pierwszym$$i$ drugim odwrotnym poziomie Zdefiniuj ${\ Displaystyle x_ {r}: = \ max (b_ {f}, b_ {s})}$ .
7. Jeśli $_$ umieszczony na $.$ Przesuń wszystkie inne przedmioty z tego poziomu niżej (wszystkie o taką samą wartość), aż pierwszy dotknie przedmiotu z pierwszego poziomu. Ponownie algorytm określa skrajną prawą parę stykających się elementów i ${\ displaystyle f'}$ i ${\ displaystyle s'}$ . zdefiniuj ${\ displaystyle h_ {2}}$ jako wielkość przesunięcia półki w dół.
   1. Jeśli ${\ Displaystyle h_ {2} \ leq h (s)}$$następnie$ przesuń w , aż dotknie innego elementu lub granicy paska. Zdefiniuj trzeci poziom u góry ${\ displaystyle s'}$ .
   2. h ${\ Displaystyle h_ {2}> h (s)}$ następnie przesuń $\ displaystyle s}$ zdefiniuj trzeci poziom na górze ${\ displaystyle s'}$ . Umieść $lewej$ na tym trzecim poziomie, tak aby dotykał elementu z pierwszego poziomu po jego lewej stronie.
8. Kontynuuj pakowanie przedmiotów przy użyciu heurystyki First-Fit. Każdy następny poziom (zaczynając od poziomu trzeciego) jest określony przez poziomą linię przechodzącą przez górę największego elementu na poprzednim poziomie. Zwróć uwagę, że pierwszy przedmiot umieszczony na następnym poziomie może nie dotykać krawędzi paska lewą stroną, ale przedmiot z pierwszego poziomu lub przedmiot ${\ displaystyle s}$ .

Ten algorytm ma następujące właściwości:

• Czas działania może być ograniczony przez ${\ Displaystyle {\ mathcal {O}} (| {\ mathcal {I}} | ^ {2}$ ) ${\ Displaystyle | {\ mathcal {I}} |}$ poziomów.
• Dla każdego zestawu elementów tworzy opakowanie o wysokości $({\ mathcal {I}}) \ leq 2OPT({\mathcal {I}})}$$ja$ .

Algorytm Steinberga (ST)

Algorytm Steinberga jest algorytmem rekurencyjnym. Biorąc $pod$ uwagę zestaw prostokątnych elementów prostokątny region docelowy o szerokości $z$ wysokości , proponuje cztery reguły redukcji, które umieszczają niektóre $.$ elementy i pozostawia mniejszy prostokątny obszar o takich samych właściwościach jak poprzednio w odniesieniu do pozostałych elementów. Rozważ następujące zapisy: Biorąc $pod$ uwagę zestaw elementów, oznaczamy przez ${\ Displaystyle h _ {\ max} ({\ mathcal {I}})}$ najwyższa wysokość elementu w ${\ Displaystyle {\ mathcal {I}}}$ , ${\ Displaystyle w_ {\ max} ( {\ mathcal {I}}}}$ największa szerokość elementu występująca w $:$ ZA ${\ Displaystyle \ operatorname {OBSZAR} ({\ mathcal {I}}): = \ suma _ {i \ in {\ mathcal {I}}} w (i) h (i)} całkowity obszar tych elementów$ . Steinbergs pokazuje, że jeśli

${\ Displaystyle h _ {\ max} ({\ mathcal {I}}) \ równoważnik H}$ , ${\ Displaystyle w_ {\ max} ({\ mathcal {ja }})\leq W}$ , i ${\ Displaystyle \ operatorname {OBSZAR} ({\ mathcal {I}}) \ równoważnik W \ cdot H- (2h _ {\ max} ({\ mathcal {I}}) -h) _ {+} (2w_ {\ max} ({\ mathcal {I}}) -W) _ {+}} gdzie$ ( ${\ Displaystyle (a) _ {+}: =\max\{0,a\}}$ ,

wtedy wszystkie elementy można umieścić w regionie docelowym o rozmiarze ${\ Displaystyle W \ razy H}$ . Każda reguła redukcji stworzy mniejszy obszar docelowy i podzbiór elementów, które należy umieścić. Gdy warunek z powyższego jest spełniony przed rozpoczęciem procedury, to utworzony podproblem również będzie miał tę właściwość.

Procedura 1 : Można ją zastosować, jeśli ${\ Displaystyle w _ {\ max} ({\ mathcal {I}}') \ geq W/2}$ .

1. Znajdź wszystkie elementy o szerokości $ja ∈ ja {\ Displaystyle i \ in {\ mathcal {$$2}$ i usuń je z $} \ Displaystyle {\ mathcal {I}}}$ .
2. Posortuj je według nierosnącej szerokości i umieść wyrównane do lewej na dole regionu docelowego. Niech $wysokością$ .
3. Znajdź wszystkie elementy o szerokości $)$$Hh_ {0}}$ . Usuń je z $\$ umieść w nowym zestawie $displaystyle {\ mathcal {I}} _ {H}$ }
4. Jeśli $pusty$ , zdefiniuj nowy region docelowy jako obszar powyżej tj. ma wysokość $H-h_ {0}}$$displaystyle$$\$ i szerokość ${\ Displaystyle W}$ . Rozwiąż problem składający się z tego nowego regionu docelowego i zredukowanego zestawu elementów za pomocą jednej z procedur.
5. Jeśli $umieść elementy dokładnie$ jeden po drugim w prawym górnym rogu obszaru docelowego. Niech $.$ całkowitą szerokością tych elementów $Zdefiniuj$ nowy obszar docelowy $w$ wysokości lewym Rozwiąż problem składający się z tego nowego regionu docelowego i zredukowanego zestawu elementów za pomocą jednej z procedur.

Procedura 2 : Można ją zastosować, jeśli spełnione są następujące warunki: ${\ Displaystyle w _ {\ max} ({\ mathcal {I}}) \ równoważnik W/2}$ , ${\ Displaystyle h _ {\ max} ({\ mathcal {I}}) \ równoważnik H / 2}$ i istnieją dwa różne elementy ${\ Displaystyle i, i'\ in {\mathcal {I}}}$ z ${\ Displaystyle w (i) \ geq W/4}$ , ${\ Displaystyle w (i') \ geq W/4}$ , $i$ 2 $_$ _ ${\ Displaystyle 2 (\ operatorname {OBSZAR} ({\ mathcal {I}}) -w (i) h (i) -w (i') h (i')} \ równoważnik (W- \ max \ {w (i),w(i')\})H}$ .

1. Znajdź i usuń je z $\ displaystyle {$$I}}$${$ .
2. Umieść szerszą w lewym dolnym rogu obszaru docelowego, a węższą wyrównaną do lewej na górze pierwszej.
3. Zdefiniuj nowy obszar docelowy po prawej stronie tych obu elementów, tak aby miał szerokość ${\ Displaystyle W- \ max \ {w (i), w ( i') \}}$ i wysokość ${\ displaystyle H}$ .
4. Umieść pozostałe elementy w $docelowym,$ korzystając z jednej z procedur.

Procedura 3 : Można ją zastosować, jeśli spełnione są następujące warunki: ${\ Displaystyle w _ {\ max} ({\ mathcal {I}}) \ równoważnik W/2}$ , ${\ Displaystyle h _ {\ max} ({\ mathcal {I}}) \ równoważnik H / 2$${\ Displaystyle | {\ mathcal {I}}|> 1}$ | , a podczas sortowania elementów według zmniejszania szerokości istnieje indeks ${\ Displaystyle m}$ tak, że definiując $pierwsze$ elementy $utrzymuje$ , ${\ Displaystyle \ operatorname {OBSZAR} ({\ mathcal {I}}) - WH / 4 \ równoważnik \ operatorname {OBSZAR} ({\ mathcal {I'}}) \ równoważnik 3WH / 8} jak$ również ${\ Displaystyle w (i_ {m + 1}) \ równoważnik W / 4}$

1. Ustaw ${\ Displaystyle W_ {1}: = \ max {W / 2,2 \ operatorname {OBSZAR} ({\ mathcal {ja' }})/H}}$ .
2. $docelowe,$ jeden w lewym dolnym rogu oryginalnego, o wysokości $}$ szerokości, a po lewej stronie o wysokości $}$${\ displaystyle$ i szerokość ${\ Displaystyle WW_ {1}}$ .
3. Użyj jednej z procedur, aby umieścić elementy w pierwszym nowym obszarze docelowym, a elementy w ${\mathcal {I'}}}$$Displaystyle$$mathcal {I}} \$ do drugiego.

Należy zauważyć, że procedury od 1 do 3 mają wersję symetryczną podczas zamiany wysokości i szerokości elementów oraz obszaru docelowego.

Procedura 4 : Można ją zastosować, jeśli spełnione są następujące warunki: ${\ Displaystyle w _ {\ max} ({\ mathcal {I}}) \ równoważnik W/2}$ , ${\ Displaystyle h _ {\ max} ({\ mathcal {I}}) \ równoważnik H / 2}$ i istnieje element ${\ Displaystyle i \ in {\ mathcal {I}} }$ takie, że ${\ Displaystyle w (i) h (i) \ geq \ operatorname {OBSZAR} ({\ mathcal {I}}) -WH / 4}$ .

1. Umieść przedmiot w lewym dolnym rogu obszaru docelowego i usuń go z . ${\ displaystyle {\ mathcal {I}$$}$ .
2. $,$$obszar docelowy na prawo$ tak aby miał szerokość wysokość umieść pozostałe elementy w tym obszarze, korzystając z .

Ten algorytm ma następujące właściwości:

• Czas działania może być ograniczony przez ${\ Displaystyle {\ mathcal {O}} (| {\ mathcal {ja }}|\log(|{\mathcal {I}}|)^{2}/\log(\log(|{\mathcal {I}}|))}}$ .
• Dla każdego zestawu elementów tworzy opakowanie o wysokości $}) \ leq 2OPT({\mathcal {I}})}$$ja$ .

Algorytmy aproksymacji czasu pseudowielomianowego

Aby poprawić dolną granicę $.$ , rozważono algorytmy czasu pseudowielomianowego dla problemu pakowania Rozważając tego typu algorytmy, wszystkie rozmiary elementów i paska są podawane jako całki. Ponadto szerokość paska $.$ pojawiać się wielomianowo w czasie działania Zauważ, że nie jest to już uważane za czas działania wielomianu, ponieważ w danym przypadku szerokość paska wymaga rozmiaru kodowania ${\ Displaystyle \ log (W)}$ .

Algorytmy czasu pseudowielomianowego, które zostały opracowane, w większości wykorzystują to samo podejście. Pokazano, że każde rozwiązanie optymalne można uprościć i przekształcić w takie, które ma jedno ze stałej liczby struktur. Algorytm następnie iteruje wszystkie te struktury i umieszcza elementy wewnątrz przy użyciu programowania liniowego i dynamicznego. Najlepszy dotychczas osiągnięty stosunek to ${\ Displaystyle (5/4 + \ varepsilon) OPT (I)}$ . podczas gdy nie może istnieć pseudo-wielomianowy algorytm czasu ze stosunkiem lepszym niż ${\ Displaystyle 5/4}$ chyba że ${\ Displaystyle P = NP}$

Przegląd przybliżeń czasu pseudowielomianowego

Rok	Współczynnik przybliżenia	Źródło	Komentarz
2010	${\ Displaystyle (3/2 + \ varepsilon)}$	Jansen, Thöle
2016	${\ Displaystyle (7/5+ \ varepsilon)}$	Nadiradze, Wiese
2016	${\ Displaystyle (4/3+ \ varepsilon)}$	Gálvez, Grandoni, Ingala, Khan	także przy obrotach o 90 stopni
2017	${\ Displaystyle (4/3+ \ varepsilon)}$	Jansen, Rau
2019	${\ Displaystyle (5/4+ \ varepsilon)}$	Jansen, Rau	również do obrotu o 90 stopni i ciągłych prac formowalnych

Algorytmy internetowe

W internetowym wariancie pakowania paskowego przedmioty docierają z czasem. Kiedy pojawia się przedmiot, należy go umieścić bezpośrednio przed poznaniem następnego przedmiotu. Rozważono dwa rodzaje algorytmów online. W pierwszym wariancie niedozwolona jest zmiana opakowania po umieszczeniu przedmiotu. W drugim przypadku przedmioty mogą zostać przepakowane, gdy pojawi się inny przedmiot. Ten wariant nazywa się modelem migracji.

Jakość algorytmu online jest mierzona (bezwzględnym) współczynnikiem konkurencyjności

${\ Displaystyle \ operatorname {sup} _ {I} A (ja) / OPT (ja)$ ,

gdzie $_$ rozwiązaniu $odpowiada$ _ Oprócz bezwzględnego współczynnika konkurencyjności zbadano asymptotyczny współczynnik konkurencyjności algorytmów online. Na przykład ${\ Displaystyle I}$ z ${\ Displaystyle h _ {\ max} (I) \ równoważnik 1}$ jest zdefiniowany jako

${\ Displaystyle \ lim \ operatorname {sup} _ {OPT (I) \ rightarrow \ infty} A (I) / OPT (ja)}$ .

Zauważ, że wszystkie przypadki można skalować tak, że ${\ Displaystyle h _ {\ max} (I) \ równoważnik 1}$ .

Przegląd algorytmów online bez migracji

Rok	Współczynnik konkurencyjności	Asymptotyczny współczynnik konkurencyjności	Źródło
1983	6,99	${\ Displaystyle \ około 1,7}$	Bakera i Schwarza
1997		${\ Displaystyle 1,69+ \ varepsilon}$	Csirika i Woegingera
2007	6.6623		Hurinka i Paulusa
2009	6.6623		Ye, Han i Zhang
2007		${\ Displaystyle 1,58889}$	Han i in. + Seiden

Ramy Han i in. ma zastosowanie w ustawieniach online, jeśli algorytm pakowania bin online należy do klasy Super Harmonic. Zatem algorytm pakowania bin online firmy Seiden Harmonic++ implikuje algorytm pakowania pasków online ze współczynnikiem asymptotycznym 1,58889.

Przegląd dolnych granic algorytmów online bez migracji

Rok	Współczynnik konkurencyjności	Asymptotyczny współczynnik konkurencyjności	Źródło	Komentarz
1982	${\ Displaystyle 2}$		Browna, Bakera i Katseffa
2006	2.25		Johannes	dotyczy również problemu z szeregowaniem zadań równoległych
2007	2.43		Hurinka i Paulusa	dotyczy również problemu z szeregowaniem zadań równoległych
2009	2.457		Kerna i Paulusa
2012		${\ displaystyle 1,5404}$	Balogh i Békési	dolna granica ze względu na leżący u podstaw problem z pakowaniem do pojemników
2016	2.618		Yu, Mao i Xiao