Produkt krańcowy kapitału

W ekonomii krańcowy produkt kapitału (MP _K ) to dodatkowa produkcja, której doświadcza firma, dodając dodatkową jednostkę kapitału. Jest cechą funkcji produkcji , obok nakładów pracy.

Definicja

Krańcowy produkt kapitału (MP _K ) to dodatkowa produkcja wynikająca, ceteris paribus ^{(„wszystko jest równe”)} , z wykorzystania dodatkowej jednostki kapitału rzeczowego , takiej jak maszyny lub budynki używane przez przedsiębiorstwa.

Krańcowy produkt kapitału (MPK) to ilość dodatkowej produkcji, jaką firma uzyskuje z dodatkowej jednostki kapitału przy stałej ilości pracy:

{\ Displaystyle MP_ {K} = F (K + 1, L) -F (K, L)}

Tak więc krańcowy produkt kapitału jest różnicą między wielkością produkcji wytworzonej przy użyciu K + 1 jednostek kapitału a wielkością produkcji przy użyciu tylko K jednostek kapitału.

Określenie krańcowego produktu kapitału jest niezbędne, gdy firma zastanawia się, czy zainwestować w dodatkową jednostkę kapitału. Decyzja o zwiększeniu produkcji jest korzystna tylko wtedy, gdy MP _K jest wyższy niż koszt kapitału każdej dodatkowej jednostki. W przeciwnym razie, jeśli koszt kapitału jest wyższy, firma będzie tracić zysk przy dodawaniu dodatkowych jednostek kapitału rzeczowego. Pojęcie to jest równe odwrotności przyrostowego stosunku kapitału do produkcji . Matematycznie jest to pochodna cząstkowa funkcji produkcji w odniesieniu do kapitału. Jeśli wielkość produkcji ${\ Displaystyle Y = f (K, L)}$ , to

{\ Displaystyle MP_ {K} = {\ Frac {{\ tekst {zmiana}} Y} {{\ tekst {zmiana} } K}} = {\ frac {\ częściowe f (K, L)} {\ częściowe K}}}

Malejące marginalne zyski

Jednym z kluczowych założeń ekonomii jest malejąca stopa zwrotu , czyli krańcowy produkt kapitału jest dodatni, ale maleje w poziomie kapitału zapasowego, czyli matematycznie

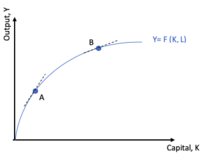
{\ Displaystyle {\ Frac {\ częściowy} {\ częściowy K}} MP_ {K} = {\ Frac {\ częściowy ^ {2} f(K,L)}{\częściowe K^{2}}}<0}

Produkcja jako funkcja nakładów kapitałowych

Graficznie dowód ten można zaobserwować na krzywej pokazanej na wykresie, która przedstawia wpływ kapitału K na produkt Y. Jeśli wielkość nakładu pracy L jest stała, nachylenie krzywej w dowolnym przypomina krańcowy produkt kapitału. W przypadku małej ilości kapitału, takiej jak punkt A, nachylenie jest bardziej strome niż w punkcie B ze względu na malejące zwroty z kapitału. Innymi słowy, dodatkowa jednostka kapitału ma malejącą produktywność, gdy wzrost produkcji staje się coraz mniej znaczący, wraz ze wzrostem K.

Przykład

Rozważmy firmę meblarską, w której nakład pracy, to znaczy liczbę pracowników, podaje się jako stałą, a nakład kapitału przekłada się na liczbę maszyn jednej z jej fabryk. Gdyby firma nie miała maszyn, nie produkowałaby mebli. Gdyby w fabryce była jedna maszyna, powstałoby szesnaście mebli. Kiedy są dwie maszyny, powstaje dwadzieścia osiem mebli. Jednak wraz ze wzrostem liczby dostępnych maszyn zmiana wydajności okazuje się mniej znacząca w porównaniu z poprzednią liczbą. Fakt ten można zaobserwować w produkcie krańcowym, który zaczyna się zmniejszać: malejących krańcowych przychodach . Jest to uzasadnione tym, że na dodatkowych maszynach nie ma wystarczającej liczby pracowników, więc wartość, jaką te dodatkowe jednostki wnoszą do firmy, w zakresie generowanej produkcji, zaczyna maleć.

Liczba maszyn	Produkcja (meble produkowane dziennie)	Produkt krańcowy kapitału
0	0	0
1	16	16
2	28	12
3	39	11
4	46	7
5	49	3
6	50	1

Stopa dzierżawy kapitału

Na doskonale konkurencyjnym rynku firma będzie dokładać kapitał do momentu, w którym MP _K zrówna się ze stopą wynajmu kapitału, co nazywamy punktem równowagi. Fakt ten uzasadnia, dlaczego na doskonale konkurencyjnych rynkach kapitałowych cenę kapitału można postrzegać jako stawkę czynszu. Cena kapitału jest określana na rynku kapitałowym przez odpowiedni popyt i podaż kapitału.

Krańcowy produkt kapitału określa rzeczywistą cenę wynajmu kapitału. Realna stopa procentowa, stopa amortyzacji i względna cena dóbr kapitałowych określają koszt kapitału. Zgodnie z modelem neoklasycznym firmy inwestują, jeśli cena wynajmu jest wyższa niż koszt kapitału, i dezinwestycje, jeśli cena wynajmu jest niższa niż koszt kapitału.

MRP _K , MC _K i maksymalizacja zysku

Firmie opłaca się zwiększanie kapitału tylko wtedy, gdy krańcowy produkt przychodu z kapitału, MRP _K (zmiana całkowitego przychodu, gdy następuje zmiana jednostkowa nakładów kapitałowych, ∆TR/∆K) jest wyższy niż koszt krańcowy kapitału, MC _K (na przykład krańcowy koszt uzyskania i użytkowania maszyny). Zatem zysk firmy osiągnie punkt maksymalny, gdy MRP _K = MC _K .

Zobacz też

Źródła

Nicholsona, Waltera (1978). Teoria mikroekonomiczna: podstawowe zasady i rozszerzenia (wyd. 2). Hinsdale: Dryden Press. s. 182–188. ISBN 0-03-020831-9 .
Robinson, R. Clark. „Krańcowy produkt pracy i kapitału” (PDF) . Materiały informacyjne dla klasy Northwestern University . Zarchiwizowane od oryginału (PDF) w dniu 9 września 2006 r.