Przepisywanie wykresu

W informatyce transformacja grafów lub przepisywanie grafów dotyczy techniki algorytmicznego tworzenia nowego wykresu z oryginalnego wykresu. Ma wiele zastosowań, począwszy od inżynierii oprogramowania ( konstruowanie oprogramowania , a także weryfikacja oprogramowania ) po algorytmy układu i generowanie obrazów.

Transformacje grafów mogą być używane jako abstrakcja obliczeniowa. Podstawową ideą jest to, że jeśli stan obliczeń można przedstawić jako wykres, dalsze kroki w tym obliczeniu można następnie przedstawić jako reguły transformacji na tym wykresie. Reguły takie składają się z grafu oryginalnego, który ma być dopasowany do podgrafu w stanie kompletnym oraz grafu zastępującego, który zastąpi dopasowany podgraf.

Formalnie system przepisywania wykresów zwykle składa $L}$ z zestawu reguł przepisywania wykresów w postaci , przy czym $\ displaystyle$ jest nazywany wykresem wzorca (lub lewą stroną) ${\ displaystyle R}$ nazywany wykresem zastępczym (lub prawą stroną reguły). Reguła przepisywania grafów jest stosowana do grafu macierzystego poprzez wyszukiwanie wystąpienia grafu wzorcowego ( dopasowywanie wzorców , rozwiązując w ten sposób problem izomorfizmu podgrafu ) i zastępując znalezione wystąpienie instancją grafu zastępczego. Reguły przepisywania można dalej regulować w przypadku grafów oznaczonych , na przykład w gramatykach grafów regulowanych łańcuchami.

Czasami gramatyka grafów jest używana jako synonim systemu przepisywania grafów , zwłaszcza w kontekście języków formalnych ; inne sformułowania służą podkreśleniu celu konstrukcji, jakim jest wyliczenie wszystkich grafów z jakiegoś grafu startowego, czyli wygenerowanie języka grafów – zamiast po prostu przekształcenia danego stanu (grafu macierzystego) w nowy stan.

Podejścia do przepisywania grafów

U góry: przykładowa reguła przepisywania grafu ( optymalizacja z konstrukcji kompilatora: mnożenie przez 2 zastąpione przez dodawanie). Dół: Zastosowanie reguły do ​​optymalizacji „y=x*2” do „y=x+x”.

Podejście algebraiczne

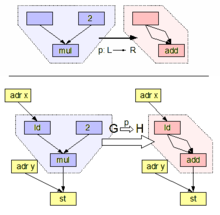
Algebraiczne podejście do przepisywania grafów opiera się na teorii kategorii . Podejście algebraiczne jest dalej podzielone na podejścia podrzędne, z których najczęstszymi są podejście podwójnego wypychania (DPO) i podejście pojedynczego wypychania (SPO) . Inne podejścia podrzędne obejmują podejście sesqui-pushout i pullback .

Z punktu widzenia podejścia DPO reguła przepisywania grafów to para morfizmów w kategorii grafów i homomorfizmy grafów między nimi: ${\ Displaystyle r = (L \ leftarrow K \ rightarrow R) }$ , również napisane , gdzie $\ Displaystyle L \ supseteq K \$ iniekcyjne $R$ . Graf K nazywany jest niezmiennym lub czasami wykresem klejenia . Krok przepisywania gdzie lub zastosowanie reguły r do $D$ hosta G jest przez dwa diagramy wypychania , oba tego samego morfizmu , jest kontekstowym ( stąd nazwa double -pushout). Inny morfizm grafu $wystąpienie L$ w G i nazywa dopasowaniem . Praktyczne zrozumienie tego jest takie, że $\ displaystyle R}$ to podgraf, który jest dopasowany z (patrz $) , a po$ izomorfizmu podgrafu $znalezieniu$ dopasowania zostaje zastąpiony przez $displaystyle L}$$\$ na wykresie hosta sol $\ displaystyle G}$ gdzie ${\ displaystyle K}$ służy jako interfejs zawierający węzły i krawędzie, które są zachowywane podczas stosowania reguły. Wykres $, aby dołączyć$$dopasowywany$ wzór do jego kontekstu: jeśli jest pusty, dopasowanie może oznaczać tylko cały połączony .

W przeciwieństwie do tego, reguła przepisywania grafów w podejściu SPO jest pojedynczym morfizmem w kategorii oznaczonych multigrafów i mapowań częściowych , które zachowują strukturę multigrafu: ${\ displaystyle r \ okrężnica L \ rightarrow R}$ . Zatem krok przepisywania jest definiowany przez pojedynczy wypychania . Praktyczne rozumienie tego jest podobne do podejścia DPO. Różnica polega na tym, że nie ma interfejsu między grafem macierzystym G a grafem G' będącym wynikiem etapu przepisywania.

Z praktycznego punktu widzenia kluczową różnicą między DPO i SPO jest sposób, w jaki radzą sobie z usuwaniem węzłów z sąsiednimi krawędziami, w szczególności w jaki sposób unikają sytuacji, w której takie usunięcia mogą pozostawić „wiszące krawędzie”. Podejście DPO usuwa węzeł tylko wtedy, gdy reguła określa również usunięcie wszystkich sąsiednich krawędzi (ten wiszący warunek można sprawdzić dla danego dopasowania), podczas gdy podejście SPO po prostu usuwa sąsiednie krawędzie, bez konieczności wyraźnej specyfikacji.

Istnieje również inne algebraiczne podejście do przepisywania grafów, oparte głównie na algebrze Boole'a i algebrze macierzy, zwane gramatyką grafów macierzowych .

Określ przepisywanie grafu

Jeszcze inne podejście do przepisywania grafów, znane jako przepisywanie grafów zdeterminowanych , wywodzi się z logiki i teorii baz danych . W tym podejściu grafy traktowane są jako instancje bazy danych, a operacje przepisywania jako mechanizm definiowania zapytań i widoków; w związku z tym wymagane jest, aby każde przepisywanie dawało unikalne wyniki ( aż do izomorfizmu ), a osiąga się to poprzez jednoczesne stosowanie dowolnej reguły przepisywania na całym wykresie, gdziekolwiek ma to zastosowanie, w taki sposób, że wynik jest rzeczywiście jednoznacznie zdefiniowany.

Przepisywanie wykresu terminowego

Innym podejściem do przepisywania grafów jest przepisywanie grafów terminów , które obejmuje przetwarzanie lub przekształcanie grafów terminów (znanych również jako abstrakcyjne grafy semantyczne ) za pomocą zestawu reguł przepisywania składni.

semantykę operacyjną kompilatora . Grafy terminowe są również używane jako abstrakcyjne maszyny zdolne do modelowania obliczeń chemicznych i biologicznych, a także rachunków graficznych, takich jak modele współbieżności. Wykresy terminów mogą przeprowadzać automatyczną weryfikację i programowanie logiczne, ponieważ dobrze nadają się do przedstawiania skwantyfikowanych stwierdzeń w logice pierwszego rzędu. Oprogramowanie do programowania symbolicznego to kolejna aplikacja do grafów terminów, które są w stanie przedstawiać i wykonywać obliczenia za pomocą abstrakcyjnych struktur algebraicznych, takich jak grupy, pola i pierścienie.

Konferencja TERMGRAPH skupia się w całości na badaniach nad przepisywaniem grafów terminowych i jego zastosowaniami.

Klasy gramatyki grafów i system przepisywania grafów

Systemy przepisywania grafów w naturalny sposób grupują się w klasy w zależności od rodzaju reprezentacji grafów, które są używane i sposobu wyrażania przepisywania. W klasyfikacjach najczęściej używany jest termin gramatyka grafów , inaczej równoważny systemowi przepisywania grafów lub systemowi zastępowania grafów . Niektóre popularne typy to:

• Gramatyka grafów przypisywanych , zwykle sformalizowana przy użyciu podejścia pojedynczego wypychania lub podejścia podwójnego wypychania do charakteryzowania zamienników, o której mowa w powyższej sekcji dotyczącej algebraicznego podejścia do przepisywania grafów.
• Gramatyki hipergrafów, w tym jako bardziej restrykcyjne podklasy gramatyk grafów portowych, gramatyk grafów liniowych i sieci interakcji .

Wdrożenia i aplikacje

Grafy to ekspresyjny, wizualny i matematycznie precyzyjny formalizm służący do modelowania obiektów (bytów) powiązanych relacjami; obiekty są reprezentowane przez węzły, a relacje między nimi przez krawędzie. Węzły i krawędzie są zwykle wpisywane i przypisywane. Obliczenia opisywane są w tym modelu poprzez zmiany relacji między encjami lub zmiany atrybutów elementów grafu. Są one zakodowane w regułach przepisywania/transformacji grafów i wykonywane przez systemy przepisywania grafów/narzędzia do transformacji grafów.

• Narzędzia, które są neutralne dla domeny aplikacji:
  • AGG , system gramatyki grafów z atrybutami ( Java )
  • GP 2 to język programowania do obliczeń na grafach poprzez ukierunkowane stosowanie reguł transformacji grafów.
  • GMTE , Graph Matching and Transformation Engine do dopasowywania i transformacji wykresów . Jest to implementacja rozszerzenia algorytmu Messmera z wykorzystaniem C++ .
  • GrGen.NET , generator przepisywania wykresów, narzędzie do transformacji wykresów emitujące kod C# lub zestawy .NET
  • GROOVE , oparty na Javie zestaw narzędzi do edycji grafów i reguł transformacji grafów, eksploracji przestrzeni stanów gramatyk grafów i sprawdzania modelu tych przestrzeni stanów; może być również używany jako silnik transformacji wykresów.
  • Verigraph , specyfikacja oprogramowania i system weryfikacji oparty na przepisywaniu wykresów ( Haskell ).
• Narzędzia rozwiązujące zadania inżynierii oprogramowania (głównie MDA ) z przepisywaniem grafów:
  • eMoflon , zgodne z EMF narzędzie do transformacji modeli z obsługą Story-Driven Modeling i Triple Graph Grammars
  • EMorF system przepisywania wykresów oparty na EMF , wspierający transformację w miejscu i model do modelu
  • Fujaba wykorzystuje modelowanie oparte na historii, język przepisywania wykresów oparty na PROGRES
  • Bazy danych wykresów często obsługują dynamiczne przepisywanie wykresów
  • Świetnie
  • Gremlin , język programowania oparty na grafach (patrz Przepisywanie wykresów )
  • Henshin , system przepisywania wykresów oparty na EMF , wspierający transformację w miejscu i model do modelu , analizę par krytycznych i sprawdzanie modeli
  • PROGRES , zintegrowane środowisko i język bardzo wysokiego poziomu dla PROgrammed Graph REwriting Systems
  • VIATRA
• Narzędzia inżynierii mechanicznej
  • GraphSynth to środowisko interpretera i interfejsu użytkownika do tworzenia nieograniczonej gramatyki grafów oraz testowania i wyszukiwania wynikowego wariantu językowego. Zapisuje wykresy i reguły gramatyki grafów jako pliki XML i jest napisany w języku C# .
  • Soley Studio to zintegrowane środowisko programistyczne dla systemów transformacji grafów. Jego głównym obszarem zastosowania jest analiza danych w dziedzinie inżynierii.
• Zastosowania biologiczne
  • Funkcjonalno-strukturalne modelowanie roślin za pomocą języka opartego na gramatyce grafowej
  • Modelowanie rozwoju wielokomórkowego za pomocą gramatyk grafowych regulowanych łańcuchowo
• Sztuczna inteligencja/przetwarzanie języka naturalnego
  • OpenCog zapewnia podstawowy mechanizm dopasowywania wzorców (na hipergrafach ), który służy do implementacji różnych algorytmów AI.
  • RelEx to anglojęzyczny parser, który wykorzystuje ponowne pisanie wykresów w celu przekształcenia analizy łącza w analizę zależności .
• Język programowania komputerów
  • Język programowania Clean jest realizowany za pomocą przepisywania grafów.

Zobacz też

• Teoria grafów
• Gramatyka kształtu
• Gramatyka formalna
• Przepisywanie abstrakcyjne — uogólnienie przepisywania grafów

Źródła

•   Rozenberg, Grzegorz (1997), Handbook of Graph Grammar and Computing by Graph Transformations , tom. 1–3, World Scientific Publishing, ISBN 9810228848 .
•   Perez, PP (2009), Matrix Graph Grammars: An Algebraic Approach to Graph Dynamics , VDM Verlag , ISBN 978-3-639-21255-6 .
• Heckel, R. (2006). Transformacja wykresu w pigułce . Notatki elektroniczne w informatyce teoretycznej 148 (1 SPEC. ISS.), s. 187–198.
• König, Barbara (2004). Analiza i weryfikacja systemów o dynamicznie zmieniającej się strukturze . Rozprawa habilitacyjna, Universität Stuttgart , s. 65–180.
•   Lobo, Daniel; Vico, Francisco J.; Dassow, Jürgen (2011-10-01). „Gramatyka grafów z przepisywaniem regulowanym ciągiem” . Informatyka teoretyczna . 412 (43): 6101–6111. doi : 10.1016/j.tcs.2011.07.004 . ISSN 0304-3975 .
•   Grzegorz Rozenberg , wyd. (luty 1997). Fundamenty . Podręcznik gramatyk grafów i informatyki przez transformację grafów . Tom. 1. Światowa nauka. doi : 10.1142/3303 . ISBN 978-981-02-2884-2 .
•   Hartmut Ehrig ; Grzegorz Engels; Hansa-Jörga Kreowskiego ; Grzegorz Rozenberg, red. (październik 1999). Aplikacje, języki i narzędzia . Podręcznik gramatyk grafów i informatyki przez transformację grafów . Tom. 2. Światowa nauka. doi : 10.1142/4180 . ISBN 978-981-02-4020-2 .
•   Hartmut Ehrig; Hansa-Jörga Kreowskiego; Ugo Montanari; Grzegorz Rozenberg, red. (sierpień 1999). Współbieżność, równoległość i dystrybucja . Podręcznik gramatyk grafów i informatyki przez transformację grafów . Tom. 3. Światowa nauka. doi : 10.1142/4181 . ISBN 978-981-02-4021-9 .