Rearanżacja drzew

Rearanżacje drzew to deterministyczne algorytmy służące do poszukiwania optymalnej struktury drzewa . Można je zastosować do dowolnego zestawu danych, które są naturalnie ułożone w drzewo, ale mają większość zastosowań w filogenetyce obliczeniowej , zwłaszcza w przeszukiwaniu drzew filogenetycznych z maksymalną oszczędnością i największym prawdopodobieństwem , które mają na celu zidentyfikowanie jednego spośród wielu możliwych drzew, które najlepiej wyjaśniają ewolucyjna historia określonego genu lub gatunku .

Podstawowe rearanżacje drzew

  • Nearest neighbor interchange (NNI)

    Węzeł najbliższego sąsiada (NNI)

  • Subtree pruning and regrafting (SPR)

    Przycinanie i ponowne szczepienie poddrzew (SPR)

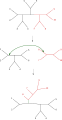
  • Tree bisection and reconnection (TBR)

    Bisekcja drzewa i ponowne połączenie (TBR)

Najprostsze przegrupowanie drzewa, znane jako wymiana najbliższego sąsiada , polega na wymianie łączności czterech poddrzew w obrębie głównego drzewa. Ponieważ istnieją trzy możliwe sposoby łączenia czterech poddrzew, a jednym z nich jest pierwotna łączność, każda wymiana tworzy dwa nowe drzewa. Wyczerpujące przeszukiwanie możliwych najbliższych sąsiadów dla każdego możliwego zestawu poddrzew jest najwolniejszym, ale najbardziej optymalizującym sposobem przeprowadzania tego wyszukiwania. Alternatywne, szersze wyszukiwanie, przycinanie poddrzew i ponowne szczepienie (SPR), wybiera i usuwa poddrzewo z głównego drzewa i ponownie umieszcza je w innym miejscu głównego drzewa, aby utworzyć nowy węzeł. Wreszcie, przecięcie i ponowne połączenie drzewa (TBR) odłącza poddrzewo od głównego drzewa w węźle wewnętrznym, a następnie próbuje wszystkich możliwych połączeń między krawędziami dwóch utworzonych w ten sposób drzew. Rosnąca złożoność techniki rearanżacji drzew koreluje z rosnącym czasem obliczeniowym wymaganym do wyszukiwania, chociaż niekoniecznie z ich wydajnością.

SPR można dalej podzielić na uSPR: Unrooted SPR, rSPR: Rooted SPR. uSPR jest stosowany do nieukorzenionych drzew i wygląda następująco: złamać dowolną krawędź. Połącz jeden koniec krawędzi (wybrany arbitralnie) z dowolną inną krawędzią w drzewie. rSPR jest stosowany do ukorzenionych drzew* i działa: złam dowolną krawędź z wyjątkiem krawędzi prowadzącej do węzła głównego. Połącz jeden koniec krawędzi (konkretnie: koniec krawędzi NAJDALEJ od korzenia) i przymocuj go do dowolnej innej krawędzi drzewa.

* W tym przykładzie korzeń drzewa jest oznaczony węzłem stopnia pierwszego, co oznacza, że ​​wszystkie węzły w drzewie mają stopień 1 lub stopień 3. Alternatywnym podejściem, zastosowanym w Bordewich i Semple, jest rozważenie węzła głównego jako mieć stopień 2 i mieć specjalną zasadę dla rSPR.

Liczbę ruchów SPR lub TBR potrzebnych do przejścia z jednego drzewa na drugie można obliczyć, tworząc Las Maksymalnej Zgodności zawierający (odpowiednio) ukorzenione lub nieukorzenione drzewa. Ten problem jest NP trudny, ale możliwy do rozwiązania z ustalonymi parametrami.

Fuzja drzew

Najprostszy rodzaj fuzji drzew zaczyna się od dwóch drzew już zidentyfikowanych jako prawie optymalne; w związku z tym najprawdopodobniej większość ich węzłów jest poprawna, ale może nie być w stanie poprawnie rozwiązać poszczególnych „liści” drzewa; na przykład separacja ((A, B), (C, D)) na końcu gałęzi w porównaniu z ((A, C), (B, D)) może być nierozwiązana. Fuzja drzew zamienia te dwa rozwiązania między dwoma skądinąd prawie optymalnymi drzewami. Warianty metody wykorzystują standardowe algorytmy genetyczne ze zdefiniowaną funkcją celu do zamiany wysoko punktowanych poddrzew na główne drzewa, które ogólnie mają wysoką punktację.

Wyszukiwanie sektorowe

Alternatywną strategią jest odłączenie części drzewa (którą można wybrać losowo lub przy użyciu bardziej strategicznego podejścia) i wykonanie TBR/SPR/NNI na tym poddrzewie. To zoptymalizowane poddrzewo można następnie zastąpić w głównym drzewie, miejmy nadzieję, poprawiając wynik p.

Dryfujące drzewo

Aby uniknąć uwięzienia w lokalnych optymach, można zastosować podejście „symulowanego wyżarzania”, w którym algorytm może czasami uwzględniać nieoptymalne drzewa kandydujące, z prawdopodobieństwem związanym z tym, jak daleko są one od optimum.

Łączenie drzew

Po zebraniu szeregu równie optymalnych drzew często można znaleźć lepsze drzewo, łącząc „dobre fragmenty” oddzielnych drzew. Podgrupy o identycznym składzie, ale innej topologii można przełączać i oceniać powstałe drzewa.

  1. ^ a b Felsenstein J. (2004). Wnioskowanie Phylogenies Sinauer Associates: Sunderland, MA.
  2. ^ Takahashi K, Nei M. (2000). Efektywność szybkich algorytmów wnioskowania filogenetycznego zgodnie z kryteriami maksymalnej oszczędności, minimalnej ewolucji i maksymalnego prawdopodobieństwa, gdy używana jest duża liczba sekwencji. Mol Biol Evol. 17(8):1251-8.
  3. ^ Bordewich M, Semple C. 2005. O złożoności obliczeniowej ukorzenionego poddrzewa przycinania i ponownego przeszczepu odległości Ann. Grzebień. 8:409–23
  4. Bibliografia _ Algorytmika, 74, 1019–1054
  5. ^ CHEN, J., wentylator, J.-H. i SZE, S.-H. 2015. Algorytmy sparametryzowane i aproksymacyjne dla lasu maksymalnej zgodności w drzewach rozgałęzionych. Informatyka teoretyczna, 562, 496–512.
  6. ^ Matsuda H. (1996). Wnioskowanie filogenetyczne białek przy użyciu maksymalnego prawdopodobieństwa za pomocą algorytmu genetycznego. Pacific Symposium on Biocomputing 1996 , s. 512-23.
  7. ^ abc Goloboff , P. (1999). Analizowanie dużych zbiorów danych w rozsądnym czasie: rozwiązania dla Composite Optima. Kladystyka, 15 (4), 415–428. doi : 10.1006/odziany.1999.0122
Pobrano z „ https://en.wikipedia.org/w/index.php?title=Tree_rearrangement&oldid=1124804136 ”