Formuła zysku Masona

Wzór wzmocnienia Masona (MGF) to metoda znajdowania funkcji przenoszenia liniowego wykresu przepływu sygnału (SFG). Formuła została wyprowadzona przez Samuela Jeffersona Masona , którego imieniem jest również nazwana. MGF to alternatywna metoda znajdowania algebraicznej funkcji przenoszenia poprzez etykietowanie każdego sygnału, zapisywanie równania zależności tego sygnału od innych sygnałów, a następnie rozwiązywanie wielu równań dla sygnału wyjściowego w odniesieniu do sygnału wejściowego. MGF zapewnia krok po kroku metodę uzyskiwania funkcji przenoszenia z SFG. Często MGF można określić na podstawie kontroli SFG. Metoda może z łatwością obsługiwać SFG z wieloma zmiennymi i pętlami, w tym pętlami z pętlami wewnętrznymi. MGF pojawia się często w kontekście systemów sterowania mikrofalami obwody i filtry cyfrowe, ponieważ są one często reprezentowane przez SFG.

Formuła

Formuła zysku jest następująca:

${\ Displaystyle G = {\ Frac {y _ {\ tekst {na zewnątrz}}} {y _ {\ tekst {w}}}} = {\ Frac {\sum _{k=1}^{N}{G_{k}\Delta _{k}}}{\Delta \ }}}$

${\ Displaystyle \ Delta = 1- \ suma L_ {i} + \ suma L_ {i} L_ {j} - \ suma L_ {i} L_ {j} L_ {k} + \ cdots + (-1)^{m}\suma \cdots +\cdots }$

Gdzie:

• Δ = wyznacznik wykresu.
• y _in = zmienna węzła wejściowego
• y _out = zmienna węzła wyjściowego
• G = całkowite wzmocnienie między _wejściem y a _wyjściem y
• N = całkowita liczba ścieżek do przodu między _wejściem y a _wyjściem y
• G _k = wzmocnienie ścieżki k- tej ścieżki do przodu między y _w i y _{na zewnątrz}
• L _i = wzmocnienie pętli dla każdej zamkniętej pętli w systemie
• L _i L _j = iloczyn wzmocnień pętli dowolnych dwóch niestykających się pętli (brak wspólnych węzłów)
• L _i L _j L _k = iloczyn wzmocnień pętli dla dowolnych trzech niestykających się par pętli
• Δ _k = wartość kofaktora Δ dla k ^-tej ścieżki do przodu, z usuniętymi pętlami stykającymi się z k ^-tą ścieżką do przodu. *

Definicje

• Ścieżka: ciągły zestaw gałęzi pokonywanych w kierunku, który wskazują.
• Ścieżka do przodu: Ścieżka od węzła wejściowego do węzła wyjściowego, w której żaden węzeł nie jest dotykany więcej niż raz.
• Pętla: Ścieżka rozpoczynająca się i kończąca w tym samym węźle, w którym żaden węzeł nie został dotknięty więcej niż raz.
• Zysk ścieżki: iloczyn zysków wszystkich gałęzi na ścieżce.
• Wzmocnienie pętli: iloczyn wzmocnień wszystkich gałęzi w pętli.

Procedura znalezienia rozwiązania

1. Sporządź listę wszystkich ścieżek do przodu i ich korzyści i oznacz te G _k .
2. Sporządź listę wszystkich pętli i ich wzmocnień i oznacz te L _{i (} pętle for i ). Sporządź listę wszystkich par niestykających się pętli i iloczynów ich zysków ( L _i L _j ). Sporządź listę wszystkich parami niestykających się pętli wykonanych po trzy na raz ( L _i L _j L _k ), następnie cztery na raz i tak dalej, aż nie będzie ich więcej.
3. Oblicz wyznacznik Δ i kofaktory Δ _k .
4. Zastosuj formułę.

Przykłady

Obwód zawierający dwa porty

Wykres przepływu sygnału obwodu zawierającego dwa porty. Ścieżka do przodu od wejścia do wyjścia jest pokazana innym kolorem.

Pożądana V2 _jest funkcja przenoszenia z V _do .

Jest tylko jedna ścieżka do przodu:

• V _do V ₁ do ja ₂ do V ₂ ze wzmocnieniem $\,}$ y

Istnieją trzy pętle:

• V ₁ do ja ₁ do V ₁ ze wzmocnieniem ${\ Displaystyle L_ {1} = - R _ {\ tekst {w}} y_ {11} \,}$
• V ₂ do ja ₂ do V ₂ ze wzmocnieniem ${\ Displaystyle L_ {2} = - R_ {L} y_ {22} \,}$
• V ₁ do ja ₂ do V ₂ do ja ₁ do V ₁ ze wzmocnieniem ${\ Displaystyle L_ {3} = y_ {21} R_ {L} y_ {12} R_ {\ tekst{w}}\,}$

${\ Displaystyle \ Delta = 1- (L_ {1} + L_ {2} + L_ {3}) + (L_ {1} }L_{2})\,}$ uwaga: L ₁ i L ₂ nie stykają się ze sobą, podczas gdy L ₃ styka się z obiema pozostałymi pętlami.

${\ Displaystyle \ Delta _ {1} = 1 \,}$ uwaga: ścieżka do przodu dotyka wszystkich pętli, więc pozostaje tylko 1 .

${\ Displaystyle G = {\ Frac {G_ {1} \ Delta _ {1}} {\ Delta}} = {\ Frac {-y_ {21} R_ {L}} {1 + R_ {\ tekst {w} }y_{11}+R_{L}y_{22}-y_{21}R_{L}y_{12}R_{\text{in}}+R_{\text{in}}y_{11}R_{ L}y_{22}}}\,}$

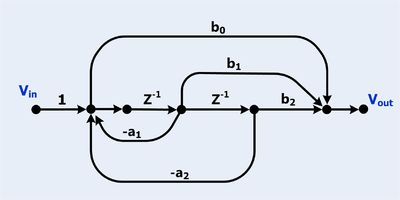
Cyfrowy filtr biquadowy IIR

Wykres przepływu sygnału (SFG) dla cyfrowego filtru bi-quad o nieskończonej odpowiedzi impulsowej. Ten SFG ma trzy ścieżki do przodu i dwie pętle.

Filtry cyfrowe są często przedstawiane jako wykresy przepływu sygnału.

Istnieją dwie pętle

• ${\ Displaystyle L_ {1} = - a_ {1} Z ^ {- 1} \,}$
• ${\ Displaystyle L_ {2} = - a_ {2} Z ^ {- 2} \,}$

${\ Displaystyle \ Delta = 1- (L_ {1} + L_ {2}) \,}$ Uwaga: dwie pętle stykają się, więc nie ma określenia na ich iloczyn.

Istnieją trzy ścieżki do przodu

• ${\ Displaystyle G_ {0} = b_ {0} \,}$
• ${\ Displaystyle G_ {1} = b_ {1} Z ^ {- 1} \,}$
• ${\ Displaystyle G_ {2} = b_ {2} Z ^ {- 2} \,}$

Wszystkie ścieżki do przodu dotykają wszystkich pętli, więc ${\ Displaystyle \ Delta _ {0} = \ Delta _ {1} = \ Delta _ {2} = 1 \,}$

${\ Displaystyle G = {\ Frac {G_ {0} \ Delta _ {0} + G_ {1} \ Delta _ {1} + G_ {2} \ Delta _ { 2}}{\Delta }}\,}$

${\ Displaystyle G = {\ Frac {b_ {0} + b_ {1} Z ^ {-1} + b_ {2} Z ^ {-2 }}{1+a_{1}Z^{-1}+a_{2}Z^{-2}}}\,}$

Serwo

Wykres położenia kątowego serwomechanizmu i przepływu sygnału. θ _C = polecenie żądanego kąta, θ _L = rzeczywisty kąt obciążenia, K _P = wzmocnienie pętli położenia, V _{ω C} = polecenie prędkości, V _ωM = napięcie czujnika prędkości silnika, K _V = wzmocnienie pętli prędkości, V _IC = polecenie prądu, V _IM = napięcie wykrywania prądu, K _C = wzmocnienie pętli prądowej, V _A = napięcie wyjściowe wzmacniacza mocy, V _M = skuteczne napięcie na indukcyjności, L _M = indukcyjność silnika, I _M = prąd silnika, R _M = rezystancja silnika, R _S = rezystancja czujnika prądu, K _M = stała momentu obrotowego silnika ( Nm /amp ), T = moment obrotowy, M = moment bezwładności wszystkich obracających się elementów α = przyspieszenie kątowe, ω = prędkość kątowa, β = tłumienie mechaniczne, G _M = stała EMF silnika wstecznego, G _T = stała wzmocnienia konwersji tachometru. Istnieje jedna ścieżka do przodu (pokazana innym kolorem) i sześć pętli sprzężenia zwrotnego. Wał napędowy w założeniu miał być na tyle sztywny, aby nie traktować go jak sprężynę. Stałe są pokazane na czarno, a zmienne na fioletowo.

Wykres przepływu sygnału ma sześć pętli. Oni są:

• ${\ Displaystyle L_ {0} = - {\ Frac {\ beta} {sM}} \,}$

• ${\ Displaystyle L_ {1} = {\ Frac {- (R_ {M} + R_ {S})} {sL_ {M}}} \,} L$

• $\ Displaystyle L_ {2} = \ ,{\frac {-G_{M}K_{M}}{s^{2}L_{M}M}}}$

• ${-K_ {C} R_ {S}} {sL_ {M}}} \,$

• ${\ Displaystyle L_ {4} = {\ Frac {-K_ {V} K_ {C} K_ {M} G_ {T}} {s ^ {2} L_ {M} M}} \, }$

• ${\ Displaystyle L_ {5} = {\ Frac {-K_ {P} K_ {V} K_ {C} K_ {M}} {s ^ {3} L_ {M} M}} \,}$

${\ Displaystyle \ Delta = 1- (L_ {0} + L_ {1} + L_ {2 }+L_{3}+L_{4}+L_{5})+(L_{0}L_{1}+L_{0}L_{3})\,}$

Jest jedna ścieżka do przodu:

• ${\ Displaystyle g_ {0} = {\ Frac {K_ {P} K_ {V} K_ {C} K_ {M}} {s ^ {3} L_{M}M}}\,}$

Ścieżka do przodu dotyka wszystkich pętli, dlatego współczynnik jest ${\ Displaystyle \ Delta _ {0} = 1}$

A zysk z wejścia na wyjście wynosi $_ {C}}} = {\ Frac {g_ {0} \ Delta _{0}}{\Delta}}\,}$

Równoważna postać macierzy

Regułę Masona można przedstawić w prostej formie macierzowej. Załóżmy, że $} = \ lewo [\ mathbf {T} \ prawej] _ {nm }}$ przejściową macierzą wykresu, gdzie $Displaystyle$ to suma transmitancji gałęzi od węzła m do węzła n . Wtedy zysk z węzła m do węzła n wykresu jest równy ${\ Displaystyle u_ {nm} = \ lewo [\ mathbf {U} \ prawo] _ {nm}}$ gdzie

${\ Displaystyle \ mathbf {U} = \ lewo (\ mathbf {I} - \ mathbf {T} \ prawej) ^ {- 1}}$ ,

i $.$ macierzą tożsamości

Reguła Masona jest również szczególnie przydatna do wyprowadzania funkcji transferu domeny Z w sieciach dyskretnych, które mają wewnętrzne pętle sprzężenia zwrotnego osadzone w zewnętrznych pętlach sprzężenia zwrotnego (pętle zagnieżdżone). Jeśli dyskretną sieć można narysować jako wykres przepływu sygnału, wówczas zastosowanie reguły Masona da funkcję przenoszenia H (z) tej sieci w domenie z.

Złożoność i aplikacje obliczeniowe

Reguła Masona może rosnąć silniowo, ponieważ liczba ścieżek w grafie skierowanym rośnie dramatycznie. Aby to zobaczyć $,$ rozważ pełny skierowany wykres na , mający krawędź między każdą parą wierzchołków. Istnieje ścieżka od ${\ displaystyle y _ {\ tekst {in}}}$ do ${\ displaystyle y _ {\ text {out}}}$ dla każdego z ${\ displaystyle (n-2)!}$ Permutacje wierzchołków pośrednich. Zatem Eliminacja Gaussa jest bardziej wydajna w ogólnym przypadku.

Jednak reguła Masona charakteryzuje funkcje przenoszenia połączonych systemów w sposób, który jest jednocześnie algebraiczny i kombinatoryczny, pozwalając na ogólne stwierdzenia i inne obliczenia w teorii systemów algebraicznych. Chociaż podczas eliminacji Gaussa występuje wiele odwrotności, reguła Masona w naturalny sposób łączy je w jedną quasi-odwrotność . Ogólna forma jest

${\ Displaystyle {\ Frac {p} {1-q}}}$

$opisano$ powyżej, jest sumą produktów cyklicznych, z których każdy zazwyczaj mieści się w ideale (na przykład operatory ściśle przyczynowe). Ułamki tej postaci tworzą podpierścień wymiernego pola funkcyjnego ${\ Displaystyle R (1 + \ langle L_ {i} \ rangle) ^ {- 1}}$ . Ta obserwacja przenosi się do przypadku nieprzemiennego, mimo że sama reguła Masona musi zostać zastąpiona przez Reguła Riegle'a .

Zobacz też

• Wykres przepływu sygnału
• Reguła Riegle'a

Notatki

• Bolton, W. Newnes (1998). Kieszonkowy podręcznik Control Engineering . Oksford: Newnes.
• Van Valkenburg, ME (1974). Analiza sieci (wyd. 3). Englewood Cliffs, NJ: Prentice-Hall.