Reguła punktacji

Wizualizacja oczekiwanego wyniku przy różnych przewidywaniach z niektórych typowych funkcji oceniania. Przerywana czarna linia: prawdziwe przekonanie prognosty, czerwona: liniowa, pomarańczowa: sferyczna, fioletowa: kwadratowa, zielona: logarytmiczna.

W teorii decyzji reguła punktacji zapewnia sumaryczną miarę oceny przewidywań lub prognoz probabilistycznych . Ma zastosowanie do zadań $prawdopodobieństwa$ w których przewidywania przypisują prawdopodobieństwa zdarzeniom, tj. jako przewidywanie wydaje się rozkład . Obejmuje to probabilistyczną klasyfikację zestawu wzajemnie wykluczających się wyników lub klas .

Z drugiej strony $się$ punktacji zapewnia sumaryczną miarę do oceny przewidywań punktowych , tj . przewiduje właściwość lub funkcję , taką jak .

Reguły punktacji i funkcje punktacji można traktować jako „funkcję kosztu” lub „ funkcję straty ”. Ocenia się je jako średnią empiryczną danej próby, zwaną po prostu wynikiem. Wyniki różnych prognoz lub modeli można następnie porównać, aby stwierdzić, który model jest najlepszy.

Jeśli koszt jest nakładany proporcjonalnie do właściwej reguły punktacji, minimalny oczekiwany koszt odpowiada zgłoszeniu prawdziwego zestawu prawdopodobieństw. Właściwe zasady punktacji są stosowane w meteorologii, finansach i klasyfikacji wzorców, gdzie prognosta lub algorytm będzie próbował zminimalizować średni wynik, aby uzyskać udoskonalone, skalibrowane prawdopodobieństwa (tj. dokładne prawdopodobieństwa).

Definicja

Rozważmy $displaystyle$ przestrzeń , a σ-algebra ${\ mathcal {A}}}$ podzbiorów podzbiorów ${\ Displaystyle \ Omega}$ i wypukłą klasę ${\ displaystyle {\ mathcal {} fa}}}$ miar prawdopodobieństwa na ${\ Displaystyle (\ Omega, {\ mathcal {A}})}$ . Funkcja zdefiniowana na $przyjmująca$ wartości na rozszerzonej linii rzeczywistej ${\ Displaystyle {\ overline {\ mathbb {R}}} = [- \ infty, \ infty ]}$ , jest ${\ Displaystyle {\ mathcal {F}}}$ -quasi-całkowalne, jeśli jest mierzalne w odniesieniu do $jest$ quasi-całkowalne w odniesieniu do wszystkich . $\ mathcal {F}}}$ {

Prognoza probabilistyczna

Prognoza probabilistyczna to dowolna miara prawdopodobieństwa ${\ displaystyle F \ in {\ mathcal {F}}}$ .

Reguła punktacji

Reguła punktacji to dowolna rozszerzona funkcja o wartościach rzeczywistych taka, że $}$ ${\ Displaystyle \ mathbf {S} (F, \ cdot)}$ jest ${\ Displaystyle {\ mathcal {F}}}$ -quasi-całkowalny dla wszystkich ${\ Displaystyle F \ w {\ mathcal { F}}}$ . ${\ Displaystyle \ mathbf {S} (F, y)}$ $i$ stratę lub karę, gdy wydawana jest prognoza y $Displaystyle y\in \Omega }$ materializuje się.

Prognoza punktowa

Prognoza punktowa jest funkcjonałem, tj. mapowaniem o potencjalnie ustalonych wartościach ${\ Displaystyle F \ rightarrow T (F) \ subseteq \ Omega}$ .

Funkcja punktacji

Funkcja punktacji to dowolna funkcja o wartościach rzeczywistych gdzie ${\ Displaystyle S: \ Omega \ razy \ Omega \ rightarrow \ mathbb {R}}$ gdzie $}$ ${\ Displaystyle S (x, y$ $zostanie$ stratę lub karę, gdy prognoza $wydana$ obserwacja zmaterializuje

Orientacja

Reguły $mniejsze$ i $_$ _ większe) wartości oznaczają lepiej. Tu wyznajemy orientację negatywną, stąd skojarzenie z „stratą”.

Przykładowy średni wynik

Biorąc pod uwagę próbkę ${\ Displaystyle y_ {i}, i = 1 \ ldots n}$ i odpowiednie prognozy ${\ displaystyle F_ {i}}$ lub ${\ displaystyle x_ {i}}$ (np. prognozy z jednego modelu), średni wynik oblicza się jako

{\ Displaystyle {\ bar {\ mathbf {S}}} = {\ Frac {1} {n}} \ suma _ {i} \ mathbf {S } (F_{i},y_{i})}

Lub

{\ Displaystyle {\ bar {S}} = {\ Frac {1} {n}} \ suma _ {i} S (x_ {i}, y_ {I})}

Średnie wyniki są używane do porównywania i oceniania różnych prognoz lub modeli.

Właściwość i spójność

Ściśle właściwe zasady $i ściśle$ prognoz poprzez maksymalizację oczekiwanej ${\ displaystyle y}$ zdaje sobie sprawę (np. $\ displaystyle y = deszcz}$ ), wtedy najwyższą oczekiwaną nagrodę (najniższy wynik) uzyskuje się, podając prawdziwy rozkład prawdopodobieństwa.

Właściwe zasady punktacji

Piszemy dla oczekiwanego wyniku pod ${\ displaystyle Q \ in {\ mathcal {F}}}$

{\ Displaystyle \ mathbf {S} (F, Q) = \ int \ mathbf {S} (F, \ omega) \ operatorname {d } Q(\omega)}

Reguła punktacji jest właściwa względem ${\ Displaystyle$ ${\ mathcal {F}}}, jeśli (zakładając orientację ujemną) S {\ Displaystyle \ mathbf {S}$ }

{\ Displaystyle \ mathbf {S} (Q, Q) \ równoważnik \ mathbf {S} (F, Q)}

dla wszystkich

{\ Displaystyle F Q\in {\mathcal {F}}}

.

Jest ściśle właściwe , jeśli powyższe równanie zachodzi z równością wtedy i tylko wtedy, gdy ${\ displaystyle F = Q}$ .

Spójne funkcje punktacji

Funkcja punktacji $jest$ spójna dla funkcjonału względem klasy, jeśli S $\ displaystyle {\ mathcal {$ $}}$

S (x, Y)]}

{\ Displaystyle \ nazwa operatora {E} _ {F} [S (t, Y)] \ równoważnik \ nazwa operatora {E} _ {F}

{\ Displaystyle t \ w T (F) }

dla wszystkich

{\ Displaystyle F \ w {\ mathcal {F}}}

t i wszystkie

{\ Displaystyle x \ w \ Omega}

.

Jest ściśle spójny, jeśli jest spójny, a równość w powyższym równaniu implikuje, że ${\ displaystyle x \ in T (F)}$ .

Przykładowe zastosowanie zasad scoringowych

Reguła logarytmiczna

Przykładem prognozowania probabilistycznego jest meteorologia, w której prognosta pogody może podać prawdopodobieństwo deszczu następnego dnia. Można odnotować, ile razy podano prawdopodobieństwo 25% w długim okresie, i porównać to z rzeczywistą proporcją opadów. Jeśli rzeczywisty procent znacznie różni się od podanego prawdopodobieństwa, mówimy, że prognostyk jest źle skalibrowany . Źle skalibrowany prognostyk może zostać zachęcony do lepszej pracy dzięki premii system. System premiowy zaprojektowany wokół właściwej zasady punktacji zachęci prognosty do zgłaszania prawdopodobieństwa równego jego osobistym przekonaniom .

Oprócz prostego przypadku decyzji binarnej , takiej jak przypisanie prawdopodobieństw do „deszczu” lub „bez deszczu”, reguły punktacji mogą być stosowane dla wielu klas, takich jak „deszcz”, „śnieg” lub „bezchmurnie” lub ciągłe odpowiedzi, takie jak ilość deszczu dziennie.

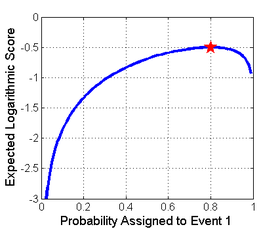
Obraz po prawej stronie pokazuje przykład reguły punktacji, logarytmicznej reguły punktacji, jako funkcji prawdopodobieństwa zgłoszonego dla zdarzenia, które faktycznie wystąpiło. Jednym ze sposobów wykorzystania tej reguły byłoby oszacowanie kosztu na podstawie prawdopodobieństwa przypisanego przez prognostę lub algorytm, a następnie sprawdzenie, które zdarzenie faktycznie ma miejsce.

Przykłady prawidłowych zasad punktacji

Oczekiwana wartość reguły logarytmicznej, gdy zdarzenie 1 ma wystąpić z prawdopodobieństwem 0,8

Istnieje nieskończona liczba reguł punktacji, w tym całe sparametryzowane rodziny ściśle odpowiednich reguł punktacji. Te pokazane poniżej to po prostu popularne przykłady.

Zmienne kategorialne

Dla kategorycznej $m$ zdarzeniami , $Displaystyle$ prognosta lub $algorytm$ zwróci $.$ prawdopodobieństwa z prawdopodobieństwem dla każdego z

Wynik logarytmiczny

Reguła punktacji logarytmicznej jest ściśle lokalną regułą punktacji. Jest to również przeczenie zaskoczenia , które jest powszechnie stosowane jako kryterium oceny we wnioskowaniu bayesowskim ; celem jest zminimalizowanie oczekiwanej niespodzianki. Ta reguła punktacji ma mocne podstawy w teorii informacji .

{\ Displaystyle L (\ mathbf {r}, ja) = \ ln (r_ {i})}

Tutaj wynik jest obliczany jako logarytm oszacowania prawdopodobieństwa rzeczywistego wyniku. Oznacza to, że prognoza 80%, która okazała się prawdziwa, otrzyma wynik $ln(0,8) = -0,22$ . Ta sama prognoza przypisuje również 20% prawdopodobieństwo przeciwnemu przypadkowi, więc jeśli prognoza okaże się fałszywa, otrzyma wynik oparty na 20%: $ln(0,2) = -1,6$ . Celem prognosty jest maksymalizacja wyniku i uzyskanie jak największego wyniku, a −0,22 jest rzeczywiście większe niż −1,6.

Jeśli prawdziwość lub fałszywość predykcji traktuje się jako zmienną $x$ o wartości odpowiednio 1 lub 0, a wyrażone prawdopodobieństwo jako $p$ , to logarytmiczną regułę punktacji można zapisać jako $x ln(p) + (1 - x) ln( 1 - p)$ . Należy zauważyć, że można użyć dowolnej podstawy logarytmicznej, ponieważ ściśle właściwe zasady punktacji pozostają ściśle właściwe w przypadku transformacji liniowej. To jest:

{\ Displaystyle L (\ mathbf {r}, i) = \ log _ {b} (r_ {i})}

jest ściśle właściwe dla wszystkich ${\ displaystyle b> 1}$ .

Wynik Brier/Kwadratowy

Kwadratowa reguła punktacji jest ściśle właściwą regułą punktacji

{\ Displaystyle Q (\ mathbf {r}, i) = 2r_ {i} - \ mathbf {r } \cdot \mathbf {r} =2r_{i}-\suma _{j=1}^{C}r_{j}^{2}}

gdzie $klas$ prawdopodobieństwo przypisane do poprawnej odpowiedzi, $to$ .

Wynik Briera , pierwotnie zaproponowany przez Glenna W. Briera w 1950 r., Można uzyskać za pomocą transformacji afinicznej z kwadratowej reguły punktacji.

{\ Displaystyle B (\ mathbf {r}, i) = \ suma _ {j = 1} ^ {C} (y_ {j }-r_{j})^{2}}

gdzie $} = 1}$ $j$ , gdy jest poprawne, aw przeciwnym razie jest ${\ Displaystyle y_ {j} = 0}$ i do ${\ displaystyle C$ liczba klas.

$,$ że prognosta powinien dążyć do maksymalizacji wyniku kwadratowego, $jednocześnie$ zminimalizować wynik . Wynika to ze znaku ujemnego w transformacji liniowej między nimi.

Reguła punktacji Hyvärinena

Funkcja punktacji Hyvärinena (o gęstości p) jest zdefiniowana przez

{\ Displaystyle s (p) = 2 \ Delta _ {y} \ log p (y) + \ |\nabla _{y}\log p(y)\|_{2}^{2}}

Gdzie oznacza $ślad$ i $oznacza$ . _ _ _ _ Ta reguła punktacji może być wykorzystana do obliczeniowego uproszczenia wnioskowania o parametrach i odniesienia się do porównania modelu bayesowskiego z arbitralnie niejasnymi priorytetami. Został również wykorzystany do wprowadzenia nowych ilości teoretycznych informacji poza istniejącą teorią informacji .

Punktacja sferyczna

Sferyczna reguła punktacji jest również ściśle właściwą regułą punktacji

{\ Displaystyle S (\ mathbf {r}, ja) = {\ Frac {r_ {i}} {\ lVert \mathbf {r} \rVert }}={\frac {r_{i}}{\sqrt {r_{1}^{2}+\cdots +r_{c}^{2}}}}}

Zmienne ciągłe

Ciągły rankingowy wynik prawdopodobieństwa

Ciągły rankingowy wynik prawdopodobieństwa (CRPS) to ściśle właściwa reguła punktacji, często używana w meteorologii. Określa się jako

${\ Displaystyle CRPS (F, y) = \ int _ {\ mathbb {R}} (F (x)-\mathbb {1} (x\geq y))^{2}dx}$

gdzie F jest prognozowaną skumulowaną funkcją $obserwacją$ .

Interpretacja właściwych zasad punktacji

Wszystkie właściwe reguły punktacji są równe sumom ważonym (całka z nieujemnym funkcjonałem wagowym) strat w zbiorze prostych dwóch alternatywnych problemów decyzyjnych, które wykorzystują prognozę probabilistyczną, przy czym każdy taki problem decyzyjny ma określoną kombinację powiązanych parametrów kosztów za decyzje fałszywie pozytywne i fałszywie negatywne . Ściśle _ właściwa reguła punktacji odpowiada posiadaniu niezerowej wagi dla wszystkich możliwych progów decyzyjnych. Każda dana właściwa reguła punktacji jest równa oczekiwanym stratom w odniesieniu do określonego rozkładu prawdopodobieństwa w progach decyzyjnych; zatem wybór reguły punktacji odpowiada założeniu o rozkładzie prawdopodobieństwa problemów decyzyjnych, dla których ostatecznie zastosowane zostaną przewidywane prawdopodobieństwa, na przykład reguła punktacji kwadratowej straty (lub Briera) odpowiadająca jednolitemu prawdopodobieństwu, że próg decyzyjny będzie gdziekolwiek między zerem a jedynką. Wynik dokładności klasyfikacji (procent poprawnie sklasyfikowany), jednoprogowa reguła punktacji, która wynosi zero lub jeden, w zależności od tego, czy przewidywane prawdopodobieństwo jest po odpowiedniej stronie 0,5, jest właściwą regułą punktacji, ale nie jest ściśle właściwą regułą punktacji, ponieważ jest zoptymalizowana (w oczekiwaniu ) nie tylko przez przewidywanie prawdziwego prawdopodobieństwa, ale przez przewidywanie dowolnego prawdopodobieństwa po tej samej stronie 0,5 co prawdziwe prawdopodobieństwo.

Porównanie ściśle właściwych zasad punktacji

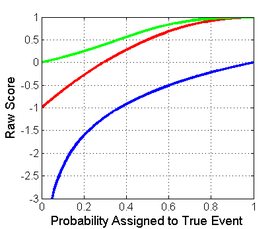
Poniżej po lewej stronie przedstawiono graficzne porównanie reguł punktacji logarytmicznej, kwadratowej i sferycznej dla problemu z klasyfikacją binarną. Oś x wskazuje zgłaszane prawdopodobieństwo zdarzenia, które faktycznie wystąpiło.

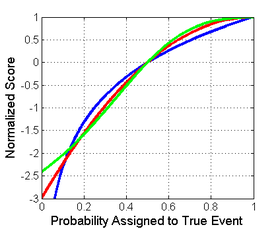
Należy zauważyć, że każdy z wyników ma inną wielkość i lokalizację. Różnice wielkości nie są jednak istotne, ponieważ wyniki pozostają prawidłowe w transformacji afinicznej. Dlatego, aby porównać różne wyniki, konieczne jest przeniesienie ich do wspólnej skali. Rozsądny wybór normalizacji pokazano na rysunku po prawej stronie, gdzie wszystkie wyniki przecinają się z punktami (0,5,0) i (1,1). Gwarantuje to, że dają one 0 dla jednolitego rozkładu (dwa prawdopodobieństwa po 0,5 każde), co nie odzwierciedla żadnych kosztów ani korzyści z raportowania, co często jest rozkładem bazowym. Wszystkie znormalizowane wyniki poniżej również dają 1, gdy prawdziwej klasie przypisano prawdopodobieństwo 1.

Wynik klasyfikacji binarnej dla prawdziwej klasy przedstawiający logarytmiczny (niebieski), sferyczny (zielony) i kwadratowy (czerwony)

Znormalizowany wynik klasyfikacji binarnej dla prawdziwej klasy przedstawiający logarytmiczny (niebieski), sferyczny (zielony) i kwadratowy (czerwony)

Charakterystyka

Transformacja afiniczna

Ściśle właściwa reguła punktacji, czy to binarna, czy wieloklasowa, po transformacji afinicznej pozostaje ściśle odpowiednią regułą punktacji. Oznacza to, że jeśli $r}, i)}$ regułą punktacji, to $\$ $a + bS ($ z ${\ displaystyle b \ neq 0}$ jest również ściśle właściwą regułą punktacji, chociaż jeśli ${\ displaystyle b <0}$ wtedy sens optymalizacji reguły punktacji przełącza się między maksymalizacją a minimalizacją.

Miejscowość

Mówimy, że właściwa reguła punktacji jest lokalna , jeśli jej oszacowanie prawdopodobieństwa określonego zdarzenia zależy tylko od prawdopodobieństwa tego zdarzenia. To stwierdzenie jest niejasne w większości opisów, ale w większości przypadków możemy myśleć o tym jako o optymalnym rozwiązaniu problemu punktacji „przy określonym zdarzeniu”, które jest niezmienne dla wszystkich zmian w rozkładzie obserwacji, które pozostawiają prawdopodobieństwo tego zdarzenia niezmienione. Wszystkie wyniki binarne są lokalne, ponieważ prawdopodobieństwo przypisane do zdarzenia, które nie wystąpiło, jest określone, więc nie ma stopnia elastyczności, który można by zmieniać.

Funkcje afiniczne logarytmicznej reguły punktacji są jedynymi ściśle właściwymi lokalnymi regułami punktacji na skończonym zbiorze, który nie jest binarny.

Rozkład

Wartość oczekiwaną właściwej reguły punktacji można rozłożyć na sumę trzech składników, zwanych niepewnością , niezawodnością i rozdzielczością , które charakteryzują różne atrybuty prognoz probabilistycznych: S {\ $S }$

{\ Displaystyle E (S) = \ operatorname {UNC} + \ operatorname {REL} - \ operatorname {RES}.}

Jeśli wynik jest właściwy i zorientowany negatywnie (taki jak wynik Briera), wszystkie trzy terminy są dodatnio określone. Składnik niepewności jest równy oczekiwanemu wynikowi prognozy, która stale przewiduje średnią częstotliwość zdarzeń. Komponent wiarygodności penalizuje źle skalibrowane prognozy, w których przewidywane prawdopodobieństwa nie pokrywają się z częstotliwościami zdarzeń.

Równania dla poszczególnych składowych zależą od konkretnej reguły punktacji. W przypadku wyniku Briera są one podawane przez

{\ Displaystyle \ operatorname {UNC} = {\ bar {x}} (1- {\ bar {x}})}

{\ Displaystyle \ operatorname {REL} = E (p- \ pi (p)) ^ {2}}

{\ Displaystyle \ operatorname {RES} = E (\ pi (p) - {\ bar {x}}) ^ {2}}

gdzie $bar {x}}}$ wystąpienia zdarzenia binarnego jest $\$ prawdopodobieństwem $Displaystyle {$ ${\ Displaystyle p}$ , tj. π $\ Displaystyle \ pi (p) = P (x = 1 \ mid p)}$

Zobacz też

Linki zewnętrzne