Rozpraszanie nośników

Typy defektów obejmują wakaty atomowe, adatomy , schodki i załamania, które występują najczęściej na powierzchniach ze względu na skończony rozmiar materiału powodujący nieciągłość kryształu. Cechą wspólną wszystkich rodzajów defektów, zarówno powierzchniowych, jak i masowych, jest to, że wytwarzają zwisające wiązania , które mają określone poziomy energii elektronów różniące się od tych w masie. Ta różnica występuje, ponieważ stanów tych nie można opisać za pomocą okresowych fal Blocha z powodu zmiany energii potencjalnej elektronów spowodowanej brakującymi rdzeniami jonowymi tuż poza powierzchnią. Są to więc stany zlokalizowane, które wymagają osobnych rozwiązań równania Schrödingera, aby można było właściwie opisać energie elektronów. Przerwa w okresowości powoduje spadek przewodnictwa z powodu rozpraszania defektów .

Elektroniczne poziomy energii zwisających wiązań półprzewodnikowych

Rysunek 1: Diagram energetyczny Harrisona energii elektronów na różnych etapach tworzenia kryształu Si. Oś pionowa to energia. Orbitale 3s i 3p hybrydyzują na jednym atomie Si, co jest niekorzystne energetycznie, ponieważ elektrony 2 3s zyskują więcej energii niż tracą elektrony 2 3p. Korzystne tworzenie dimerów tworzy stany wiązania (b) i anty-wiązania (b*), co ostatecznie prowadzi do utraty energii netto, a kolejne dodanie atomów buduje kryształy tworzące pasma przewodzenia (CB) i pasma walencyjne (VB). Zwisające stany wiązań (db) są równoważne brakującemu wiązaniu sp ³ .

Prostszym i bardziej jakościowym sposobem określania poziomów energii zwisających wiązań są diagramy Harrisona. Metale mają wiązania bezkierunkowe i małą długość Debye'a , co ze względu na ich naładowany charakter sprawia, że ​​zwisające wiązania są nieistotne, jeśli w ogóle można uznać, że istnieją. Półprzewodniki są dielektrykami , więc elektrony mogą czuć się uwięzione w defektowych stanach energetycznych. Poziomy energetyczne tych stanów są określone przez atomy tworzące ciało stałe. Rysunek 1 przedstawia schemat Harissona dla elementarnego półprzewodnika Si. wiązanie sp ^{3 , które, gdy wiele dimerów sp 3} Si-Si łączy się w celu utworzenia ciała stałego, definiuje pasma przewodnictwa i walencyjne. Gdyby istniała wakat, taka jak na każdym atomie na granicy faz ciało stałe/próżnia, skutkowałoby to co najmniej jednym zerwanym wiązaniem sp ³ , które ma energię równą energii pojedynczych samozhybrydyzowanych atomów Si, jak pokazano na rysunku 1. Energia ta odpowiada mniej więcej połowie pasma wzbronionego Si, ~0,55eV powyżej pasma walencyjnego. Z pewnością jest to najbardziej idealny przypadek, podczas gdy sytuacja byłaby inna, gdyby wystąpiła na przykład pasywacja wiązań (patrz poniżej) i rekonstrukcja powierzchni . Eksperymentalnie energie tych stanów można określić za pomocą spektroskopii absorpcyjnej lub rentgenowskiej spektroskopii fotoelektronów , na przykład, jeśli czułość instrumentu i / lub gęstość defektów są wystarczająco wysokie.

Rysunek 2: Diagram energii elektronów Harrisona dla GaAs półprzewodnikowych związków III-IV. Podobnie jak w przypadku Si, kryształ zbudowany jest z dodatkiem zhybrydyzowanych dimerów GaAs. Ponieważ wolne miejsca powodują zwisające wiązania Ga, tworzące stany w pobliżu CB. Wakaty Ga wytwarzają zwisające wiązania As o energiach bliskich VB. VB składa się głównie ze stanów „podobnych do As”, ponieważ jonowość umieszcza elektrony na atomach As, w wyniku czego stany CB są „podobne do Ga”.

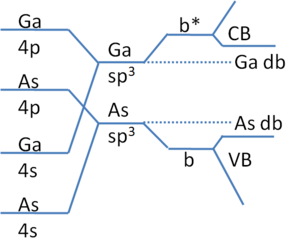
Półprzewodniki złożone, takie jak GaA, mają zwisające stany wiązań, które są bliżej krawędzi pasma (patrz rysunek 2). Ponieważ wiązanie staje się coraz bardziej jonowe, stany te mogą nawet działać jako domieszki . Jest to przyczyną dobrze znanej trudności z domieszkowaniem GaN typu p, w którym luki N są obfite ze względu na wysoką prężność par, co skutkuje wysoką gęstością zwisających wiązań Ga. Stany te znajdują się blisko krawędzi pasma przewodnictwa i dlatego działają jako dawcy. Gdy wprowadzane są domieszki akceptorowe typu p, są one natychmiast kompensowane przez wakaty N. W przypadku tych płytkich stanów ich traktowanie jest często uważane za analogiczne do atomu wodoru w następujący sposób w przypadku wakatów anionów lub kationów (efektywna masa dziury, m*, dla kationów i elektronów m* dla wakatów anionów). Energia wiązania, mi _do -E _db , to mi do $} = U + KE = {\ Frac { 1}{2}}U\;\;(1)}$ gdzie U=-q ² /(4πεε _r r) jest potencjałem elektrostatycznym między elektronem zajmującym zwisające wiązanie a jego rdzeniem jonowym przy ε, stałej przenikalności wolnej przestrzeni , ε _r , względna przenikalność i r separacja rdzenia elektron-jon. Uproszczenie, że energia translacji elektronu, KE=-U/2, wynika z twierdzenia wirialnego dla potencjałów centrosymetrycznych. Jak opisano w modelu Bohra , r podlega kwantyzacji ${\ Displaystyle n \ lambda = 2 \ pi r \; \; (2)}$ . Pęd elektronu jest p=mv=h/λ taki, że ${ \ Displaystyle KE = {\ Frac {p ^ {2}} {2m ^ {*}}} = {\ Frac {h ^ {2} n ^ {2}} {8m ^ {*} \ pi ^ {2} r^{2}}}=-{\frac {U}{2}}={\frac {q^{2}}{8\pi \varepsilon \varepsilon _{r}r}}\;\;( 3)}$ w wyniku ${\ Displaystyle r = {\ Frac {4 \ pi \ hbar ^ {2} n ^ {2} \ varepsilon \ varepsilon _{r}}{q^{2}m^{*}}}\;\;(4)}$ i ${\ Displaystyle E_ {c} -E_ {db} = {\ Frac {U} {2}} = {\ Frac {m ^ {*} q ^ {4}} {8h ^ {2} (\ varepsilon \varepsilon _{r})^{2}}}\;\;(5)}$ . Ta obróbka traci dokładność, ponieważ defekty oddalają się od krawędzi obu pasm.

Rozpraszanie defektów

Zwisające poziomy energii wiązań są wartościami własnymi funkcji falowych opisujących elektrony w pobliżu defektów. W typowym rozważaniu rozpraszania nośników odpowiada to końcowemu stanowi częstotliwości rozpraszania Fermiego : ${\ Displaystyle S_ {k'k} = {\ Frac {2 \ pi} {\ hbar}} | <f | H'| i> | ^ {2} \ delta (E_{f}-E_{i})\;\;(6)}$ gdzie H' jest parametrem interakcji, a delta Diraca δ(Ef _- Ei ₎ wskazuje na rozpraszanie sprężyste . Prosta zależność 1/τ= Σ _k',k S _k'k sprawia, że ​​równanie to jest przydatne do charakteryzowania właściwości transportu materiału, gdy jest używane w połączeniu z σ = ne ² τ /m* i regułą Matthiessena w celu uwzględnienia innych procesów rozpraszania.

Wartość S _k'k jest określona przede wszystkim przez parametr interakcji H'. Termin ten różni się w zależności od tego, czy rozważane są stany płytkie, czy głębokie. Dla stanów płytkich, H' jest składnikiem perturbacyjnym przedefiniowanego hamiltonianu H=H _o + H', przy czym H _o ma energię wartości własnej E _i . Macierz dla tego przypadku to ${\ Displaystyle <f | H'|i> \ równoważnik M_ {k 'k}={\frac {1}{V}}\int d{\bar {r}}H'e^{i{\bar {r}}({\bar {k}}-{\bar { k}}')}={\frac {1}{V}}\sum _{\bar {q}}\int d{\bar {r}}H_{\bar {q}}e^{i{ \bar {r}}({\bar {k}}-{\bar {k}}'+{\bar {q}})}={\frac {1}{V}}\sum _{\bar {q}}H_{\bar {q}}\delta _{{\bar {k}}-{\bar {k}}'},_{\bar {q}}={\frac {1}{ V}}H_{\bar {q}}\;\;(7)}$ gdzie k' jest wektorem falowym stanu końcowego, którego wartość jest tylko jedna, ponieważ gęstość defektów jest na tyle mała, że ​​nie tworzą się pasma (~<10 ¹⁰ /cm ² ). $\ Displaystyle \ nabla ^ {2} V ({\ bar {r}}) = {\ Frac {-e \ delta ({\ bar {r}} )}{\varepsilon \varepsilon _{r}}}=-\sum _{\bar {q}}{\bar {q}}^{2}V_{\bar {q}}e^{i{\ bar {q}}{\bar {r}}}={\frac {-e}{V\varepsilon \varepsilon _{r}}}\ \sum _{\bar {q}}e^{i{\ bar {q}}{\bar {r}}}\;\;(8)}$ równania , daje współczynnik Fouriera potencjału zwisającego wiązania V _q =e/(q ² εε _r V) gdzie V jest objętością. H. $Displaystyle H_ {\ bar {q}}=-eV_{\bar {q}}={\frac {-e^{2}}{{\bar {q}}^{2}\varepsilon \varepsilon _{r}V}}= {\frac {-e^{2}}{({\bar {q}}^{2}+q_{s}^{2})\varepsilon \varepsilon _{r}V}}\;\;( 9)}$ gdzie q _s to poprawka wektora falowego długości Debye'a spowodowana ekranowaniem ładunku. Wówczas częstotliwość rozpraszania wynosi ${\ Displaystyle {\ Frac {1} {\ tau}} = \ suma _ {{\ bar {k}} ', {\ bar {k}}} S _ {{\ bar {k }}'{\bar {k}}}=n\sum _{\bar {k}}{\frac {2\pi}}{\hbar }}{\frac {e^{4}\delta (E_{ \bar {k}}-E_{{\bar {k}}'})}{\varepsilon \varepsilon _{r}V[{\bar {q}}^{2}-q_{s}^{2 }]^{2}}}={\frac {ne^{4}}{4\pi ^{2}\hbar \varepsilon \varepsilon _{r}}}\int \int \int dkd\theta d\ phi {\frac {k^{2}sin\theta \;\delta (E_{\bar {k}}-E_{{\bar {k}}'})}{[{\bar {q}}^ {2}-q_{s}^{2}]^{2}}}\;\;(10)}$ gdzie n to objętościowa gęstość defektów. Wykonanie całkowania z wykorzystaniem |k|=|k'| daje ${\ Displaystyle {\ Frac {1} {\ tau}} = {\ Frac {ne ^ {4}} {2 \ pi {\ sqrt { 2m^{*}(E_{c}-E_{db})}}\hbar ^{2}\varepsilon \varepsilon _{r}}}\left({\frac {1}{q_{s}^{ 2}}}-{\frac {1}{q_{s}^{2}+{\frac {8m^{*}(E_{c}-E_{db})}{\hbar ^{2}} }}}\prawo)\;\;(11)}$ . Powyższe leczenie słabnie, gdy defekty nie są okresowe, ponieważ zwisające potencjały wiązań są reprezentowane przez szereg Fouriera. Uproszczenie sumy o współczynnik n w równaniu (10) było możliwe tylko ze względu na małą gęstość defektów. Gdyby każdy atom (a może każdy inny) miał mieć jedno zwisające wiązanie, co jest całkiem rozsądne dla niezrekonstruowanej powierzchni, to całkowanie po k' też musi być wykonane. Ze względu na zastosowanie teorii perturbacji przy definiowaniu macierzy oddziaływań powyższe zakłada małe wartości H' lub płytkie stany defektów w pobliżu krawędzi pasm. Na szczęście sama złota reguła Fermiego jest dość ogólna i może być stosowana do głębokich defektów stanu, jeśli oddziaływanie między elektronem przewodzącym a defektem jest wystarczająco dobrze zrozumiane, aby modelować ich oddziaływanie na operatora, który zastępuje H'.

Pomiary eksperymentalne

Rysunek 3: (Góra) Proste przemiatanie napięcia źródło-dren ze wzrastającą gęstością defektów może być użyte do wyodrębnienia współczynnika rozpraszania nośnika i zwisającej energii wiązania (czerwona krzywa z większą liczbą defektów). (Dół) Zależność rezystywności od temperatury. W pobliżu zera absolutnego ujawnia się waga defektów w rozpraszaniu nośników.

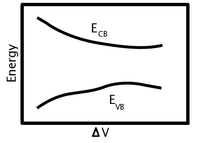
Określenie, w jakim stopniu te zwisające wiązania wpływają na transport elektryczny, można dość łatwo zaobserwować eksperymentalnie. Przesuwając napięcie wzdłuż przewodnika (rysunek 3), rezystancję i przy określonej geometrii można określić przewodnictwo próbki. Jak wspomniano wcześniej, σ = ne ² τ /m*, gdzie τ można wyznaczyć znając n i m* z pozycji poziomu Fermiego i struktury pasma materiału. Niestety, ta wartość zawiera efekty innych mechanizmów rozpraszania, takich jak fonony. Zyskuje to na użyteczności, gdy pomiar jest używany razem z równaniem (11), gdzie nachylenie wykresu 1/τ względem n umożliwia obliczenie Ec _- E _db , a punkt przecięcia wyznacza 1/τ ze wszystkich procesów rozpraszania defektów oprócz defektów. Wymaga to założenia, że ​​rozpraszanie fononów (między innymi, być może pomijalne procesy) jest niezależne od koncentracji defektów. W podobnym eksperymencie można po prostu obniżyć temperaturę przewodnika (rysunek 3), tak aby gęstość fononów spadła do znikomej wartości, pozwalając na dominującą rezystywność defektu. W tym przypadku σ = ne ² τ /m* może być użyte do bezpośredniego obliczenia τ dla rozpraszania defektów.

Pasywacja

Rysunek 4: Pasywacja wodorowa tranzystora polowego (MOSFET) typu metal-tlenek-półprzewodnik Si w celu redukcji stanów styku Si/ _SiO2 . Wiązania wodorowe z Si w pełni zadowalają hybrydyzację sp ^{3 , zapewniając zajęcie stanu defektu, zapobiegając rozpraszaniu nośnika w tych stanach.}

Defekty powierzchniowe zawsze można „pasywować” za pomocą atomów, aby celowo zajmować odpowiednie poziomy energii, tak aby elektrony przewodzące nie mogły rozpraszać się w tych stanach (skutecznie zmniejszając n w równaniu (10)). Na przykład pasywacja Si na styku kanał/tlenek tranzystora MOSFET za pomocą wodoru (Rysunek 4) jest typową procedurą pomagającą zmniejszyć gęstość defektów ~10 ¹⁰ cm ^-2 nawet o współczynnik 12, poprawiając w ten sposób mobilność, a co za tym idzie, prędkości przełączania. Usunięcie stanów pośrednich, które w przeciwnym razie zmniejszyłyby bariery tunelowania, zmniejsza również prąd upływu bramki i zwiększa pojemność bramki , a także odpowiedź przejściową. Efektem jest to, że wiązanie Si sp ³ staje się w pełni spełnione. Oczywistym wymaganiem jest tutaj zdolność półprzewodnika do utleniania pasywującego atomu lub E _c -E _db + χ > E _I , z powinowactwem elektronowym półprzewodnika χ i energią jonizacji atomu E _I .

Rozpraszanie fononów

Rozważymy teraz rozpraszanie nośników z deformacjami sieci określanymi jako fonony . Rozważ przemieszczenie objętościowe, jakie wytwarza taka rozchodząca się fala $,$$\ Delta V_{0}/V_{0}=\bigtriangledown u(r,t)}$ / gdzie prosta fala płaska jest używana do opisu propagacji fononu, ${\ Displaystyle u (r, t) \ propto exp \ pm (iqr-i \ omega t)}$ . Przemieszczenie atomów z ich pozycji równowagi generalnie powoduje zmianę struktury pasma elektronowego (Rysunek 5), gdzie w przypadku rozpraszania mamy do czynienia z elektronami w paśmie przewodnictwa o energii ~E _CB , $\ Displaystyle \ Delta E_ {CB} = {\ Frac {\ operatorname {d} E_ {CB}}{\mathrm {d} V_{0}}}\Delta V_{0}=V_{0}{\frac {\mathrm {d} E_{CB}}{\mathrm {d} V_{0 }}}{\frac {\Delta V_{0}}{V_{0}}}=Z_{DP}\cdot \bigtriangledown u(r,t)\;\;(12)}$ . Parametr empiryczny, Z _DP , nazywany jest potencjałem odkształcenia i opisuje siłę sprzężenia elektron-fonon. Mnożenie przez populację fononów ( rozkład Bosego-Einsteina , N _q ) daje całkowity potencjał deformacji, ${\ Displaystyle \ Delta E_ {CB} ^ {Tot} = {\ widehat {H}} _ { int}=Z_{DP}\cdot \bigtriangledown u(r,t){\sqrt {N_{q}+{\frac {1}{2}}\pm {\frac {1}{2}}}} =\pm iqZ_{DP}u(r,t){\sqrt {N_{q}+{\frac {1}{2}}\pm {\frac {1}{2}}}}\;\; (13)}$

Ryc. 5: Schemat zmieniających się krawędzi pasm energii (pasmo przewodnictwa, E _CB i pasmo walencyjne E _VB ), gdy pozycje atomów kryształu są przemieszczane z równowagi w celu wytworzenia odkształcenia objętościowego.

(powód rootowania będzie widoczny poniżej). Tutaj + odpowiada emisji fononów, a – absorpcji fononów podczas zdarzenia rozpraszania. Uwaga, ponieważ $podłużnymi$ fononów poprzecznych Dlatego pełna macierz interakcji to ${\ Displaystyle <k '| {\ widehat {H}} _ {int }|k>=\pm iqZ_{DP}u(r,t){\sqrt {N_{q}+{\frac {1}{2}}\pm {\frac {1}{2}}}} \ delta _ {k ', k \ pm q} \; \; (14)}$ gdzie delta Kroneckera wymusza zachowanie pędu i wynika z założenia elektronicznych funkcji falowych (stan końcowy, ${\ displaystyle <k'|}$ i stan początkowy $są$ falami płaskimi

Fonony akustyczne

Korzystając ze złotej reguły Fermiego, można w przybliżeniu oszacować współczynnik rozpraszania dla fononów akustycznych o niskiej energii. Macierz interakcji dla tych fononów to ${\ Displaystyle | <k '| {\ widehat {H}} _ {int}|k>|^{2}=Z_{DP}^{2}{\frac {\hbar \omega _{q}}{2V\rho c^{2}}}(N_{q}+ {\frac {1}{2}}\pm {\frac {1}{2}})\delta _{k',k\pm q}\;\;(15)}$ z częstotliwością kątową fononu ω _q =cq, objętość V, gęstość ciała stałego ρ i prędkość grupy fononów c. Podłączając to do Eq. 6 daje ${\ Displaystyle S_ {k'k} ^ {Ac} = {\ Frac {2 \ pi} {\ hbar}} Z_ {DP} ^ {2} {\ Frac { \hbar \omega _{q}}{2V\rho c^{2}}}(N_{q}+{\frac {1}{2}}\pm {\frac {1}{2}})\ delta _{k',k\pm q}\delta [E(k')-E(k)\pm \hbar \omega _{q}]\;\;(16)}$ . Przy założeniu, że N _q >>1, ħω<<kT i g(E') ~ g(E) (co ogólnie obowiązuje dla kryształów 3D, ponieważ energie elektronów przewodnictwa są na ogół znacznie większe niż ħω i g(E) nie ma żadnej furgonetki Osobliwość Hove'a ) daje $_ { k'}S_{k'k}^{Ac}=\suma _{k}S_{k\pm q,k}^{Ac}}$ rozpraszania: ${\ Displaystyle = {\ Frac {2 \ pi} {\ hbar}} Z_{DP}^{2}{\frac {\hbar \omega _{q}}{2V\rho c^{2}}}({\frac {kT}{\hbar \omega _{q}}} )\suma _{k}\delta _{k',k\pm q}\delta [E(k')-E(k)\pm \hbar \omega _{q}]}$${\ Displaystyle = {\ Frac {2 \ pi} {\ hbar}} Z_ {DP} ^ {2} {\ Frac {kT} {2V \ rho do ^ {2}}} V \ razy g (E)}$$\ Displaystyle = {\ Frac {\ sqrt {2}}{\pi }}{\frac {Z_{DP}^{2}m^{*{\frac {3}{2}}}kT}{\rho \hbar ^{4}c^ {2}}}{\sqrt {E-E_{CB}}}\;\;(17)}$ gdzie g(E) jest gęstością elektronową stanów , dla których otrzymano trójwymiarowe rozwiązanie z dyspersją paraboliczną ostateczna odpowiedź.

Fonony optyczne

Zazwyczaj fonony w gałęziach optycznych relacji dyspersji drgań mają energie rzędu lub większe niż kT, a zatem przybliżenia ħω<<kT i N _q >>1 nie mogą być wykonane. Jednak rozsądną drogą, która wciąż zapewnia objazd od zajmowania się złożonymi dyspersjami fononów, jest użycie modelu Einsteina , który stwierdza, że ​​​​w ciałach stałych istnieje tylko jeden tryb fononu. W przypadku fononów optycznych to przybliżenie okazuje się wystarczające ze względu na bardzo małą zmianę nachylenia ω(q), a zatem możemy twierdzić, że ħω(q) ≅ ħω jest stałą. W konsekwencji Nq _jest również stałą (zależną tylko od T). Ostatnie przybliżenie, g(E')=g(E±ħω) ~ g(E), nie może być wykonane od ħω ~ E i nie ma na to obejścia, ale dodatkowa złożoność sumy dla τ jest minimalna. ${\ Displaystyle {\ Frac {1} {\ tau}} = \ suma _ {k'} S_ {k'k} ^ {Op} = {\ frac { 2\pi }{\hbar }}Z_{DP}^{2}{\frac {\hbar \omega }{2V\rho c^{2}}}(N_{q}+{\frac {1}{ 2}}\pm {\frac {1}{2}})\suma _{k'}\delta _{k',k\pm q}\delta [E(k')-E(k)\pm \ hbar \ omega ]}$${\ Displaystyle = Z_ {DP} ^ { 2}{\frac {\hbar \omega}{8\pi ^{2}\hbar \rho c^{2}}}(N_{q}+{\frac {1}{2}}\pm {\ frac {1}{2}})g(E\pm \hbar \omega)\;\;(18)}$ . Suma zamienia się w gęstość stanów w E ', a rozkład Bosego-Einsteina można wyjąć z sumy ze względu na ħω (q) ≅ ħω.