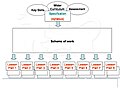
Schemat pracy

Schemat pracy określa strukturę i treść kursu akademickiego. Dzieli często wieloletni program nauczania na możliwe do dostarczenia jednostki pracy, z których każda trwa znacznie krócej (np. dwa lub trzy tygodnie). Każda jednostka pracy jest następnie analizowana na możliwe do nauczenia indywidualne tematy o jeszcze krótszym czasie trwania (np. dwie godziny lub mniej).

Lepsze schematy pracy wyraźnie określają, w jaki sposób zasoby (np. książki, sprzęt, czas) i zajęcia klasowe (np. wykład nauczyciela, praca w grupach, ćwiczenia, dyskusje) oraz strategie oceniania (np. testy, quizy, pytania i odpowiedzi, prace domowe ) będą wykorzystywane do uczyć każdego tematu i oceniać postępy uczniów w nauce materiału związanego z każdym tematem, jednostką i schematem pracy jako całości. Oczekuje się, że w miarę postępów uczniów w ramach schematu pracy poprawi się ich postrzeganie powiązań między tematami i jednostkami.

Schematy pracy mogą zawierać godziny i daty (terminy) realizacji poszczególnych elementów programu nauczania. Filozoficznie wiąże się to z przekonaniem, że wszyscy uczniowie powinni mieć dostęp do wszystkich elementów programu nauczania, tak aby ci, którzy są w stanie „dotrzymać kroku” („najlepsi” / elita), nie przegapili żadnych treści i mogli osiągnąć najwyższe stopnie. Można to określić jako pogląd „tradycjonalistyczny”.

Istnieje sprzeczny filozoficzny pogląd, że należy unikać terminów i że każda klasa powinna postępować we własnym tempie: tak, aby żaden uczeń nie został „pozostawiony w tyle”. Podczas gdy pozostali uczniowie „nadrabiają zaległości”, ci uczniowie, którzy szybko rozumieją, powinni zostać umieszczeni w „planie oczekiwania” pełnym łamigłówek i pytań, które będą dla nich wyzwaniem, aby połączyć niedawną naukę z długotrwałą nauką (można ich również zachęcić do spędzenia niewielkiej ilość czasu poprawiającego ich zrozumienie poprzez wspieranie kadry nauczycielskiej w usuwaniu podstawowych błędów/pytań kolegów, którzy nie uchwycili tak szybko ostatnich pomysłów). Ten pogląd można opisać jako podejście „opanowania”. W nauczaniu matematyki w Anglii jest ono silnie wspierane przez finansowane przez rząd Narodowe Centrum Doskonałości w Nauczaniu Matematyki w oparciu o badania prowadzone na podstawie wyjątkowych na skalę światową wyników szkół w Singapurze i Szanghaju.

Program

Schemat pracy jest zwykle interpretacją specyfikacji lub programu nauczania i może być używany jako przewodnik w trakcie kursu, aby monitorować postępy w stosunku do pierwotnego planu. Schematy pracy można udostępnić studentom, aby mieli przegląd swojego kursu.

Ostatecznym źródłem specyfikacji lub programu nauczania jest program nauczania. Programy nauczania są zazwyczaj określane przez rząd, a zatem przez prawo i/lub regulacje. W związku z tym każdy kraj ma swoje własne (chociaż niektóre kraje decydują się na przyjęcie programów nauczania określonych przez inne kraje).

Przy generowaniu planu pracy należy szczegółowo uwzględnić program nauczania wymagany prawnie w kraju, w którym plan pracy ma być realizowany. Są one zazwyczaj szczegółowo definiowane według tematu. Zrozumienie subtelności i niuansów ich prezentacji ma kluczowe znaczenie przy definiowaniu najbardziej użytecznych schematów pracy.

Anglia

W przypadku utrzymywanych szkół i komisji egzaminacyjnych w Anglii, Departament Edukacji ustala Narodowy Program Nauczania w taki sposób, aby wszystkie dzieci dorastające w Anglii miały zasadniczo podobne wykształcenie.

Program nauczania dla szkół podstawowych (w wieku od 4/5 do 11 lat) i szkół średnich (w wieku od 11 do 18 lat) w Anglii jest podzielony na pięć kluczowych etapów. Kluczowe etapy 1 i 2 realizowane są w Szkołach Podstawowych. Etapy kluczowe 3, 4 i 5 realizowane są w szkołach średnich.

Anglia - Matematyka

Angielskie szkoły podstawowe: kluczowe etapy 1 i 2 [wiek od 5 do 11 lat]

Oczekiwania dotyczące realizacji krajowego programu nauczania matematyki w Anglii na kluczowych etapach 1 i 2 są ściśle określone z jasno określonymi celami w czasie. Departament Edukacji dostarczył wstępny roczny plan pracy (lub zestaw oczekiwań) dla każdego roku szkolnego/akademickiego od klasy 1 (wiek 5/6) do klasy 6 włącznie (wiek 10/11). Nie określa to kolejności nauczania każdego tematu w każdym roku; zawiera jednak wskazówki i określa oczekiwania dotyczące tego, czego należy nauczać i czego należy się uczyć do końca każdego roku szkoły podstawowej.

Angielskie szkoły średnie: kluczowe etapy 3 i 4 [wiek od 11 do 16 lat]

Krajowy program nauczania matematyki w Anglii jest również ściśle określony na kluczowych etapach 3 i 4. Jednak wydział matematyki każdej szkoły angielskiej ma większą swobodę decydowania, kiedy i jak dostarczać treści. W przeciwieństwie do krajowego programu nauczania dla angielskich szkół podstawowych, nie ma rocznych oczekiwań. Zamiast tego wytyczne są ustalane w odniesieniu do tego, czego należy nauczać i czego należy się nauczyć do końca 3. etapu kluczowego [koniec 9. klasy (13/14 lat)] i 4. etapu kluczowego [11. wiek 15/16 lat)].

Warto zauważyć, że program nauczania dla Etapu kluczowego 4 został opracowany przez Departament Edukacji w celu zbadania całości nauczania z Etapów kluczowych od 1 do 4. W szczególności tematy wymienione w Etapie kluczowym 3 wyraźnie stanowią część programu nauczania dla Etapu kluczowego 4 (takie jak fundamenty wcześniejszego uczenia się są wzmacniane podczas budowania na nich). W związku z tym uczniowie, którzy w przeszłości zmagali się z trudniejszymi do zrozumienia elementami, mają możliwość opanowania treści etapu 3, podczas gdy inni równolegle budują wyżej.

Angielskie szkoły średnie: egzaminy GCSE [zwykle wiek 15/16+]

W Anglii obowiązkowe jest zdanie egzaminu GCSE z matematyki przed ukończeniem szesnastych urodzin.

Warto zauważyć, że treść przedmiotu uzgodniona między Departamentem Edukacji a Urzędem ds. Kwalifikacji i Egzaminów (Ofqual) [regulator komisji egzaminacyjnej dla GCSE, AS-Levels i A-Levels] jest wyróżniona w subtelny sposób odmienny od treści przedmiotu krajowego programu nauczania dla Key Stage 4.

Ten ostatni zawiera dwa poziomy oczekiwań (zwykły tekst kontra {bold i 'braces'} ); pierwszy zawiera trzy (zwykły tekst, podkreślony tekst i pogrubiony tekst ). Subtelne rozróżnienie umożliwiło bardziej spostrzegawczym uczniom, rodzicom i nauczycielom określenie (lub spekulacje na temat) sposobu, w jaki treść jest (lub powinna być) rozdzielana między dwa różne zestawy egzaminów z matematyki GCSE (podstawowy i wyższy): te dwa zestawy nakładają się (sugerując, że podkreślone tematy istnieją na przecięciu dwóch zestawów tematów).

Warto również zauważyć, że program nauczania dla GCSE jest zamierzony przez Departament Edukacji w celu zbadania całej nauki od kluczowych etapów 1 do 4. W szczególności tematy wymienione w kluczowym etapie 3 wyraźnie stanowią część programu nauczania dla kluczowego etapu 4 i GCSE ( tak, że fundamenty wcześniejszego uczenia się są wzmacniane podczas budowania na nich). W związku z tym uczniowie, którzy w przeszłości zmagali się z trudniejszymi do zrozumienia elementami, mają możliwość opanowania treści etapu 3, podczas gdy inni równolegle budują wyżej.

Angielskie szkoły średnie: AS i A-Levels [zwykle wiek 17+]

AS i A-Levels z matematyki nie są obowiązkowe.

W związku z tym w Anglii nie ma krajowego programu nauczania matematyki AS i A-Level. Istnieją jednak uzgodnione treści przedmiotowe wymagane przez Departament Edukacji dla specyfikacji AS i A z matematyki.

Elementy

Kluczowe części „planu pracy” mogą obejmować:

Treść 1

Cele lub wyniki

Metody realizacji (działania uczniów i nauczycieli)

Strategie oceniania

Zasoby

Inne Uwagi

• 

  schemat Pracy

Przykład prostego schematu pracy

Zobacz także Plany lekcji .

Schematy pracy [1]