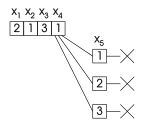
Skoki w tył

W algorytmach śledzenia wstecznego backjumping jest techniką, która zmniejsza przestrzeń wyszukiwania , zwiększając w ten sposób wydajność . Podczas gdy cofanie się zawsze idzie w górę o jeden poziom w drzewie wyszukiwania , gdy wszystkie wartości dla zmiennej zostały przetestowane, cofanie się może iść w górę o więcej poziomów. W tym $artykule$ zastosowano stałą kolejność oceny zmiennych

Drzewo wyszukiwania odwiedzane przez regularne cofanie się
Backjump: szary węzeł nie jest odwiedzany

Definicja

Ilekroć śledzenie wsteczne wypróbowało wszystkie wartości dla zmiennej bez znalezienia żadnego rozwiązania, ponownie rozważa ostatnią z wcześniej przypisanych zmiennych, zmieniając jej wartość lub kontynuując śledzenie wstecz, jeśli żadne inne wartości nie mają być wypróbowane. Jeśli ${\ Displaystyle x_ {1} = a_ {1}, \ ldots, x_ {k} = a_ {k}}$ to bieżące częściowe przypisanie i wszystkie wartości dla ${\ Displaystyle x_ {k + 1}}$ zostały wypróbowane bez znalezienia rozwiązania, cofanie się prowadzi do wniosku, że żadne rozwiązanie nie rozciąga się ${\ Displaystyle x_ {1} = a_ { 1},\ldots ,x_{k}=a_{k}}$ istnieje. Następnie algorytm „podnosi się” do $,$ wartość , jeśli to możliwe, cofając się ponownie $przeciwnym$

Częściowe przypisanie nie zawsze jest konieczne w całości, aby udowodnić, że żadna $nie$ rozwiązania W szczególności przedrostek przypisania częściowego może mieć tę samą właściwość, to znaczy $istnieje$ że ${ \ displaystyle x_ {1}, \ ldots, x_ {j} = a_ {1}, \ ldots, a_ {j}} nie można$ rozszerzyć, aby utworzyć rozwiązanie o dowolnej wartości dla ${\ displaystyle x_ {k + 1}}$ . $jak$ może bezpośrednio rozważyć inną wartość zamiast ponownego rozważenia, $normalnie$ by to


Przykład, w którym bieżące przypisanie do zostało bezskutecznie wypróbowane z każdą możliwą wartością ${1} x_ {2} x_ {3} x_ {4}$ $Displaystyle$ . $,$ się wraca do próbując przypisać mu nową wartość	Zamiast cofania się, algorytm dokonuje dalszych udoskonaleń, udowadniając, że oceny ${\ Displaystyle x_ {1} x_ {2} x_ {5} = 211}$ , ${\ Displaystyle x_ {1} x_ {2} x_ {5} = 212}$ i ${\ Displaystyle x_ {1} x_ {2} x_ {5} = 213}$ nie są częścią dowolne rozwiązanie.	W rezultacie bieżąca ocena $nie$ $rozwiązania ,$ algorytm może bezpośrednio , dla niego nową wartość.

Wydajność algorytmu backjumpingu zależy od tego, jak wysoko jest on w stanie wykonać backjumping. $jest$ idealnym przypadku algorytm mógłby przeskoczyć z $}} nie można rozszerzyć, aby$ do dowolnej zmiennej $która$ , że bieżące przypisanie do $\ displaystyle$ $x_$ rozwiązanie o dowolnej wartości . W takim przypadku nazywa się $to$ skokiem .

Ustalenie, czy skok jest bezpieczny, nie zawsze jest wykonalne, ponieważ bezpieczne skoki są definiowane w kategoriach zbioru rozwiązań, co algorytm próbuje znaleźć. W praktyce algorytmy backjumpingu wykorzystują najniższy indeks, jaki mogą skutecznie udowodnić, że jest to bezpieczny skok. Różne algorytmy stosują różne metody określania, czy skok jest bezpieczny. Metody te mają różny koszt, ale wyższy koszt znalezienia wyższego bezpiecznego skoku może zostać zastąpiony mniejszą ilością poszukiwań z powodu pomijania części drzewa poszukiwań.

Backjumping w węzłach liści

Najprostszym warunkiem, w którym możliwe jest przeskakiwanie wstecz, jest sytuacja, gdy wszystkie wartości zmiennej zostały udowodnione, że są niespójne bez dalszego rozgałęziania. W przypadku spełniania ograniczeń ocena częściowa jest spójna wtedy i tylko wtedy, gdy spełnia wszystkie ograniczenia dotyczące przypisanych zmiennych, aw przeciwnym razie jest niespójna . Może się zdarzyć, że spójnego rozwiązania częściowego nie można rozszerzyć do spójnego rozwiązania kompletnego, ponieważ niektóre z nieprzypisanych zmiennych mogą nie zostać przypisane bez naruszenia innych ograniczeń.

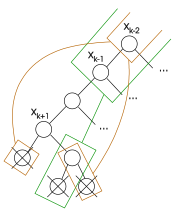
Warunek, w którym wszystkie wartości danej zmiennej $,$ $\ displaystyle$ obecnym rozwiązaniem częściowym nazywa się ślepą uliczką . Dzieje się tak dokładnie wtedy $,$ gdy zmienna jest liściem drzewa wyszukiwania (co odpowiada węzłom mającym tylko liście jako dzieci na rysunkach w

Algorytm backjumpingu autorstwa Gaschniga wykonuje backjumping tylko w ślepych zaułkach liścia. Innymi słowy, działa to inaczej niż cofanie się tylko wtedy, gdy każda możliwa wartość $.$ potrzeby rozgałęziania się nad inną zmienną

Bezpieczny skok można znaleźć po prostu oceniając dla $displaystyle x_ {1}, \ ldots, x_ {k} = a_ {1}, \ ldots, a_ {k}}$ $1$ x niezgodne z ${\ Displaystyle x_ {k + 1} = a_ {k +1}}$ . Innymi słowy, jeśli $,$ możliwą wartością dla $\ displaystyle a_ {k + 1}$ następujących ocen:

${\ Displaystyle x_ {1} = a_ {1}}$	...	${\ Displaystyle x_ {k-1} = a_ {k-1}}$	${\ Displaystyle x_ {k} = a_ {k}}$	${\ Displaystyle x_ {k + 1} = a_ {k + 1}}$
${\ Displaystyle x_ {1} = a_ {1}}$	...	${\ Displaystyle x_ {k-1} = a_ {k-1}}$		${\ Displaystyle x_ {k + 1} = a_ {k + 1}}$
...
${\ Displaystyle x_ {1} = a_ {1}}$				${\ Displaystyle x_ {k + 1} = a_ {k + 1}}$

Najmniejszy indeks (najniższy na liście), dla którego oceny są niespójne, byłby bezpiecznym skokiem, gdyby jedyną możliwą wartością był ${\ Displaystyle x_ {k + 1} = a_ {k + 1}}$ dla ${\ Displaystyle x_ {k + 1}}$ . Ponieważ każda zmienna może zwykle przyjmować więcej niż jedną wartość, maksymalny indeks wynikający ze sprawdzenia każdej wartości jest bezpiecznym skokiem i jest punktem, w którym przeskakuje algorytm Gaschniga.

$powyższe$ samym sprawdza spójność

Backjumping w węzłach wewnętrznych

Poprzedni algorytm przeskakuje wstecz tylko wtedy, gdy można pokazać wartości zmiennej niezgodne z bieżącym rozwiązaniem częściowym bez dalszego rozgałęziania. Innymi słowy, pozwala na backjump tylko w węzłach liści w drzewie wyszukiwania.

Wewnętrzny węzeł drzewa wyszukiwania reprezentuje przypisanie zmiennej zgodne z poprzednimi. Jeśli żadne rozwiązanie nie rozszerzy tego zadania, poprzedni algorytm zawsze cofa się: w tym przypadku nie wykonuje się żadnego skoku wstecz.

Skoki wsteczne w węzłach wewnętrznych nie mogą być wykonywane tak, jak w przypadku węzłów liścia. Rzeczywiście, jeśli $, że$ oceny wymagały rozgałęzienia, z bieżącym przypisaniem. W rezultacie szukanie prefiksu niezgodnego z tymi wartościami ostatniej zmiennej nie powiedzie się.

$displaystyle x_ {1}, \ ldots, x_ {k}}$ $że$ ocena nie obecną to wyszukiwanie rekurencyjne . W szczególności algorytm „wie”, że od tego momentu żadne rozwiązanie nie istnieje, ponieważ wraca do tego węzła zamiast zatrzymywać się po znalezieniu rozwiązania.

Ten powrót wynika z wielu ślepych zaułków , punktów, w których algorytm okazał się niespójnym rozwiązaniem częściowym. Aby wykonać kolejny krok wstecz, algorytm musi wziąć pod uwagę, że niemożność znalezienia rozwiązań wynika z tych ślepych zaułków. W szczególności bezpieczne skoki to indeksy przedrostków, które nadal sprawiają, że te ślepe zaułki są niespójnymi rozwiązaniami częściowymi.


W tym przykładzie algorytm powrócił do , po $wypróbowaniu$ wszystkich możliwych wartości, z powodu trzech przecinających	$,$ nawet jeśli wartości i zostaną usunięte z jego częściowej oceny (zwróć uwagę $że$ w swoich dzieciach)	Inne niespójne oceny pozostają takie nawet bez $x_ {k}}$ x $\ Displaystyle x_ {k-1}$ $i$ x	Algorytm może przeskoczyć do $,$ ponieważ jest to najniższa zmienna, która zachowuje Zostanie wypróbowana nowa wartość dla ${\ displaystyle x_ {k-2}} .$

Innymi słowy, gdy wszystkie wartości $zostały$ wypróbowane, algorytm może cofnąć się do poprzedniej zmiennej $bieżąca$ prawdziwości x ${\ displaystyle x_ {1}, \ ldots, x_ {i}} jest niespójne$ wszystkimi ocenami prawdziwości ${\ Displaystyle x_ {k + 1}, x_ {k + 2}, ...}$ w węzłach liści, które są potomkami węzła ${\ Displaystyle x_ {k + 1}}$ .

uproszczenia

Szukając możliwego przeskoku wstecz dla

.

w zacienionym obszarze można

$}}$ { \ $}$ $1$ jest zbierane podczas wizyty w jego poddrzewie. Znalezienie bezpiecznego skoku można uprościć, biorąc pod uwagę dwa czynniki. Po pierwsze, algorytm potrzebuje bezpiecznego skoku, ale nadal działa ze skokiem, który nie jest najwyższym możliwym bezpiecznym skokiem.

${$ , że węzły w poddrzewie , które zostały pominięte przez backjump, można zignorować podczas szukania backjump dla $l}}$ . Dokładniej, wszystkie węzły pominięte przez backjump od węzła $} }$ węzła $są$ nieistotne dla poddrzewa zakorzenionego w $}$ $x_ {m$ , a także nieistotne są ich inne poddrzewa.

$Rzeczywiście$ , jeśli algorytm przeszedł z węzła węzła $przez ścieżkę,$ mógł przejść bezpośrednio ${ zamiast tego \ displaystyle x_ {l}}$ do ${\ displaystyle x_ {m}}$ . Rzeczywiście, backjump $wskazuje,$ ${l}}$ węzły między i nieistotne dla poddrzewa zakorzenionego w $x_$ . Innymi słowy, backjump wskazuje, że wizyta w regionie drzewa wyszukiwania była błędem. Dlatego tę część drzewa wyszukiwania można zignorować, rozważając możliwy powrót do $z$ lub od jednego z jego przodków

Zmienne, których wartości są wystarczające do udowodnienia niespełnialności w poddrzewie zakorzenionym w węźle, są gromadzone w węźle i wysyłane (po usunięciu zmiennej z węzła) do węzła powyżej podczas wycofywania.

Fakt ten można wykorzystać, zbierając w każdym węźle zestaw wcześniej przypisanych zmiennych, których ocena wystarczy do udowodnienia, że w poddrzewie zakorzenionym w węźle nie istnieje żadne rozwiązanie. Zbiór ten jest budowany podczas wykonywania algorytmu. Podczas wycofywania się z węzła zestaw ten jest usuwany ze zmiennej węzła i gromadzony w zbiorze celu cofania się lub przeskakiwania wstecz. Ponieważ węzły pominięte podczas wykonywania skoku wstecz nigdy nie są wycofywane, ich zestawy są automatycznie ignorowane.

Backjumping oparty na wykresie

$na wykresach jest to$ sprawdzając, które ze zmiennych w ograniczeniu z zmienne ${\ Displaystyle x_ {k + 1}, x_ {k + 2},...},$ które są tworzone w węzłach liści. Dla każdego węzła liścia i każdej zmiennej indeksu $displaystyle$ $i> k}$ , która jest tam utworzona, indeksy mniejsze lub równe k, których zmienna jest równa ${\ displaystyle x_ {i}}$ w ograniczeniu z $.$ bezpieczne skoki W szczególności, gdy wypróbowano wszystkie wartości dla, ten zestaw zawiera indeksy zmiennych, których oceny pozwalają udowodnić, że nie można znaleźć rozwiązania, odwiedzając poddrzewo zakorzenione w $k + 1 {\ displaystyle x_ {k +$ ${\ displaystyle x_ {k + 1}}$ . W rezultacie algorytm może wykonać skok wsteczny do najwyższego indeksu w tym zestawie.

Fakt, że węzły pominięte przez backjumping można zignorować przy rozważaniu dalszego backjumpingu, można wykorzystać za pomocą następującego algorytmu. Podczas wycofywania się z węzła liścia tworzony jest zestaw zmiennych, które są z nim powiązane i „odsyłany z powrotem” do jego rodzica lub przodka w przypadku skoku wstecz. W każdym węźle wewnętrznym utrzymywany jest zestaw zmiennych. Za każdym razem, gdy zestaw zmiennych jest odbierany od jednego z jego dzieci lub potomków, jego zmienne są dodawane do utrzymywanego zestawu. Podczas dalszego cofania się lub cofania z węzła, zmienna węzła jest usuwana z tego zestawu, a zestaw jest wysyłany do węzła, który jest celem cofania się lub cofania. Algorytm ten działa, ponieważ zbiór utrzymywany w węźle zbiera wszystkie zmienne, które są istotne dla udowodnienia niespełnialności w liściach będących potomkami tego węzła. Ponieważ zestawy zmiennych są wysyłane tylko podczas powrotu z węzłów, zestawy zebrane w węzłach pominiętych przez backjumping są automatycznie ignorowane.

Backjumping oparty na konflikcie (inaczej backjumping ukierunkowany na konflikt (cbj))

Jeszcze bardziej wyrafinowany algorytm backjumpingu, czasami zdolny do osiągnięcia większych backjumpingów, opiera się nie tylko na sprawdzaniu wspólnej obecności dwóch zmiennych w tym samym ograniczeniu, ale także na tym, czy ograniczenie faktycznie spowodowało niespójność. W szczególności ten algorytm zbiera jedno z naruszonych ograniczeń w każdym liściu. W każdym węźle najwyższy indeks zmiennej znajdującej się w jednym z ograniczeń zebranych na liściach jest skokiem bezpiecznym.

O ile naruszone ograniczenie wybrane w każdym liściu nie wpływa na bezpieczeństwo wynikowego skoku, o tyle wybranie ograniczeń o najwyższych możliwych wskaźnikach zwiększa wysokość skoku. Z tego powodu oparte na konflikcie ograniczenia kolejności przeskakiwania wstecz w taki sposób, że ograniczenia dotyczące zmiennych o niższych indeksach są preferowane niż ograniczenia dotyczące zmiennych o wyższym indeksie.

Formalnie ograniczenie jest preferowane w stosunku do innego $,$ jeśli najwyższy indeks zmiennej w, $displaystyle$ $nie$ w, $C}$ najwyższy indeks do zmiennej $,$ ale nie $.$ Innymi słowy, wykluczając wspólne zmienne, preferowane jest ograniczenie, które ma wszystkie niższe indeksy.

$że$ algorytm wybiera najniższy indeks $z$ , ostatnią liść. Spośród ograniczeń, które są naruszone w tej ocenie, wybiera najbardziej preferowane i zbiera wszystkie swoje wskaźniki mniejsze niż ${\ displaystyle k + 1}$ . W ten sposób, gdy algorytm wraca do zmiennej $najniższy$ zebrany indeks identyfikuje

W praktyce algorytm ten jest uproszczony poprzez zebranie wszystkich indeksów w jednym zestawie, zamiast tworzenia zestawu dla każdej wartości ${\ displaystyle k}$ . W szczególności algorytm zbiera w każdym węźle wszystkie zestawy pochodzące od jego potomków, które nie zostały pominięte przez backjumping. Podczas wycofywania się z tego węzła, ten zestaw jest usuwany ze zmiennej węzła i gromadzony w miejscu docelowym cofania się lub przeskakiwania wstecz.

Skoki wsteczne ukierunkowane na konflikt zostały zaproponowane w przypadku problemów z satysfakcją z ograniczeń przez Patricka Prossera w jego przełomowym artykule z 1993 roku.

Zobacz też

Dechter, Rina (2003). Przetwarzanie ograniczeń . Morgana Kaufmanna. ISBN 1-55860-890-7 .
Prosser, Patrick (1993). „Algorytmy hybrydowe dla problemu spełnienia ograniczeń” (PDF) . Inteligencja obliczeniowa 9(3).