Stosunek mundurów

Stosunek uniformów to metoda pierwotnie zaproponowana przez Kindermana i Monahana w 1977 r. w celu próbkowania liczb pseudolosowych , to znaczy losowania próbek losowych z rozkładu statystycznego . Podobnie jak próbkowanie odrzucenia i próbkowanie z odwrotną transformacją jest to metoda dokładnej symulacji. Podstawową ideą tej metody jest wykorzystanie zmiany zmiennych w celu utworzenia ograniczonego zbioru, który można następnie równomiernie próbkować w celu wygenerowania zmiennych losowych zgodnie z pierwotnym rozkładem. Jedną z cech tej metody jest to, że rozkład na próbkę musi być znany jedynie do nieznanego współczynnika mnożenia, co jest powszechną sytuacją w statystyce obliczeniowej i fizyce statystycznej.

Motywacja

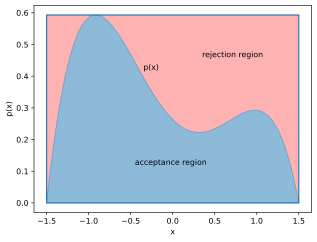
Próbkowanie odrzucone dla ograniczonego rozkładu statystycznego ze skończonym wsparciem.

Wygodną techniką próbkowania rozkładu statystycznego jest próbkowanie przez odrzucenie . Gdy funkcja gęstości prawdopodobieństwa rozkładu jest ograniczona i ma skończone wsparcie , można wokół niej zdefiniować ramkę ograniczającą (rozkład propozycji jednolitej), narysować w ramce jednolite próbki i zwrócić tylko współrzędne x punktów znajdujących się poniżej funkcji (patrz wykres). Bezpośrednią konsekwencją podstawowego twierdzenia symulacji jest rozkład zwracanych próbek według rozkładu pierwotnego.

Gdy wsparcie rozkładu jest nieskończone, nie można narysować prostokątnej ramki ograniczającej zawierającej wykres funkcji. Nadal można zastosować próbkowanie odrzucone , ale z nierównomiernym rozkładem propozycji. Wybór odpowiedniego rozkładu propozycji może być delikatny, trzeba też wiedzieć, jak skutecznie pobrać próbkę tego rozkładu propozycji.

Metoda stosunku równomierności oferuje rozwiązanie tego problemu, zasadniczo wykorzystując jako propozycję rozkładu rozkład utworzony przez stosunek dwóch jednorodnych zmiennych losowych .

Oświadczenie

Twierdzenie i dowód zostały zaadaptowane z prezentacji Gobeta

Twierdzenie - Niech $będzie$ wielowymiarową zmienną losową z funkcją gęstości prawdopodobieństwa ${2}, \ ldots, x_ {d})}$ na . ${\ displaystyle \ mathbb {R} ^ {d}$ } Funkcja musi być znana tylko do stałej, więc możemy założyć, że $znamy$ gdzie ${\ Displaystyle p (x_ {1}, x_ {2},$ $)$ , ze $lub$ trudną do obliczenia. Niech ${\ displaystyle r> 0}$ , parametr, który można dostosować, jeśli zdecydujemy się ulepszyć właściwości metody. Możemy zdefiniować zbiór : ${\ displaystyle A_ {f, r}$ }

{\ Displaystyle A_ {f, r} = \ lewo \ {(u, v_ {1}, v_ {2}, \ ldots, v_ {d}) \ in \ mathbb {R} ^ {d + 1}: 0\leq u\leq f\left({\frac {v_{1}}{u^{r}}},{\frac {v_{2}}{u^{r}}},\ldots ,{ \frac {v_{d}}{u^{r}}}\right)^{\frac {1}{1+rd}}\right\}}

Miara Lebesgue'a zbioru

r

i równa. ZA

displaystyle A_

.

Ponadto, niech ${\ displaystyle (U, V_ {1}, V_ {2}, \ ldots, V_ {d})}$ będzie zmienną losową o rozkładzie jednostajnym na ZA $r}}$ \ displaystyle A_ {f Następnie ${\ Displaystyle \ lewo ({\ Frac {V_ {1}} U ^ {r}}}, {\ Frac {V_ {2}} U ^ {r}}}, \ ldots, {\ Frac {V_$ $}$ $d}} {U ^ {r}}} \ prawo)}$ jest zmienną losową o rozkładzie podobnym . ${\ displaystyle \ mathbb {R} ^ {d}$

Dowód

Najpierw założymy, że pierwsze stwierdzenie jest poprawne, czyli ${\ Displaystyle | A_ {f, r} | = {\ Frac {1} {c \, (1+rd)}}}$ .

Niech $będzie$ mierzalną funkcją na $_$ _ Rozważmy oczekiwanie φ ( $\ Displaystyle \ varphi \ lewo ({\ Frac {V_ {1}} {U ^ {r}}}, \ ldots, {$ na zestawie ${\ displaystyle A_ {f, r}}$ :

{\ Displaystyle E \ lewo [\ varphi \ lewo ({\ Frac {V_ {1}} {U ^ {r}}}, \ ldots, {\ Frac {V_ {d}} U ^ {r}}} \right)\right]={\frac {1}{|A_{f,r}|}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty } \cdots \int _{-\infty }^{\infty }\varphi \left({\frac {v_{1}}{u^{r}}},\ldots ,{\frac {v_{d}} {u^{r}}}\right)\mathbf {1} _{(u,v_{1},\ldots,v_{d})\in A_{f,r}}\mathrm {d} u\ ,\mathrm {d} v_{1}\ldots \mathrm {d} v_{d}}

Wraz ze zmianą zmiennych mamy ${\ displaystyle x_ {i} = {\ Frac {v_ {i}} {u ^ {r}}}}$

{\ Displaystyle {\ początek {wyrównane} E \ lewo [\ varphi \ lewo ({\ Frac {V_ {1}} U ^ {r}}}, \ ldots, {\ Frac {V_ {d}} {U ^{r}}}\right)\right]&={\frac {1}{|A_{f,r}|}}\int _{-\infty }^{\infty }\int _{-\ infty }^{\infty }\cdots \int _{-\infty }^{\infty }\varphi (x_{1},\ldots ,x_{d})\mathbf {1} _{0\leq u\ leq f(x_{1},\ldots,x_{d})^{\frac {1}{1+rd}}}u^{rd}\mathrm {d} u\,\mathrm {d} x_{ 1}\cdots \mathrm {d} x_{d}\\&={\frac {1}{|A_{f,r}|}}\int _{-\infty }^{\infty }\cdots \ int _{-\infty }^{\infty }\varphi \left(x_{1},\ldots,x_{d}\right){\frac {1}{1+rd}}f\left(x_{ 1},\ldots ,x_{d}\right)\mathrm {d} x_{1}\cdots \mathrm {d} x_{d}\\&=\int _{-\infty }^{\infty } \ldots \int _{-\infty }^{\infty }\varphi \left(x_{1},\ldots ,x_{d}\right)p\left(x_{1},\ldots ,x_{d }\right)\mathrm {d} x_{1}\cdots \mathrm {d} x_{d}\end{aligned}}}

gdzie możemy to zobaczyć ${\ Displaystyle \ lewo ({\ Frac {V_ {1}} U ^ {r}}}, \ ldots, {\ Frac {V_ {d}} {U ^ {r}}} \ prawo)}$ $rzeczywiście$ gęstość .

Wracając do pierwszego stwierdzenia, podobny argument pokazuje, że ${\ Displaystyle | A_ {f, r} | = {\ Frac {1} {c \, (1+rd)}}}$ .

Uzupełnia

ZA ${\ displaystyle A_ {f, r}$

Powyższe stwierdzenie nie określa, w jaki sposób $przeprowadzić$ . Jednak zainteresowanie tą metodą polega na tym, że w łagodnych warunkach (mianowicie, że $re$ $x_{2},\ldots,x_{d})^{\frac {1}{1+rd}}}$ ${\ displaystyle f (x_ {1}, fa ( x 1 , x 2 , … , x$ i ${\ Displaystyle x_ {i} f (x_ {1}, x_ {2}, \ ldots, x_ {d}) ^ {\ Frac {r {1+rd}}}$ dla wszystkich $ograniczone$ ograniczone ) , jest . $displaystyle A_ {f, r}}$ \ Można zdefiniować prostokątną obwiednię ${\ displaystyle {\ tylda {A}} _ {f, r}}$ takie, że

{\ Displaystyle A_ {f, r} \ podzbiór {\ tylda {A}} _ {f, r} = \ lewo [0, \ sup _ {x_ {1}, \ ldots, x_ {d}} {f ( x_{1},\ldots ,x_{d})^{\frac {1}{1+rd}}}\right]\times \prod _{i}\left[\inf _{x_{1}, \ldots ,x_{d}}{x_{i}f(x_{1},\ldots ,x_{d})^{\frac {r}{1+rd}}},\sup _{x_{1 },\ldots ,x_{d}}{x_{i}f(x_{1},\ldots ,x_{d})^{\frac {r}{1+rd}}}\right]}

Pozwala to na

_

próbkowanie

poprzez _ Parametr

,

kształt

zmaksymalizować

współczynnik akceptacji tego próbkowania

ZA fa $\ displaystyle A_ {f, r}$

Definicja $jest już$ etapu próbkowania Dla celów ilustracyjnych interesujące może być narysowanie zbioru, w którym to przypadku przydatna może być znajomość parametrycznego opisu jego granicy:

{\ Displaystyle u = f \ lewo (x_ {1}, x_ {2}, \ ldots, x_ {d} \ prawo) ^ {\ Frac {1} {1+rd} }\quad {\text{and}}\quad \forall i\in [|1,n|],v_{i}=x_{i}u^{r}}

lub w typowym przypadku, gdy

\ displaystyle (u ,v)=\left(f(x)^{\frac {1}{1+r}},x\,f(x)^{\frac {r}{1+r}}\right)}

zmienną jednowymiarową,

(

.

Uogólniony stosunek mundurów

Tutaj sparametryzowany tylko za pomocą $,$ uniformów można opisać bardziej ogólną klasą transformacji.

W przypadku jednowymiarowym, jeśli jest funkcją ściśle rosnącą i różniczkowalną, taką jak ${\ displaystyle g: \ mathbb {R} ^ {+} \rightarrow \ mathbb {R} ^ {+}}$ ${\ displaystyle g (0) = 0}$ , wtedy możemy zdefiniować tak, że ${\ displaystyle A_ {f, g}}$

{\ Displaystyle A_ {f, g} = \ lewo \ {(u, v)\in \mathbb {R} ^{2}:0\leq u\leq g^{-1}\left[f\left({\frac {v}{g'(u)}}\right) \prawo]\prawo\}}

Jeśli $V)}$ $frac {V$ jest zmienną losową o równomiernym rozkładzie w V ${g'(U)}}}$ $\ displaystyle {\$ $}$ rozkłada się z .

Przykłady

Rozkład wykładniczy przed i po zmianie zmiennych metodą ilorazową uniformów.

na

: wykres rozkładu wykładniczego .

A_

} displaystyle {\ tylda {A}} _ {f, 1}}

zbiór

\ Displaystyle

przestrzeni w obwiednię ZA . Dodano kolorowe domeny o równym prawdopodobieństwie, aby pomóc w wizualnym powiązaniu odpowiednich domen przekształconych zestawów.

Rozkład wykładniczy

$_$ chcemy rozkładu wykładniczego uniformów Zajmiemy się tutaj. ${\ displaystyle r = 1}$ .

Możemy rozpocząć konstruowanie zestawu ${\ displaystyle A_ {f,1}$ }

{\ Displaystyle A_ {f, 1} = \ lewo \ {(u, v) \ in \ mathbb {R} ^{2}:0\leq u\leq {\sqrt {p\left({\frac {v}}\right)}}\right\}}

Warunek jest równoważny, po obliczeniu, ${\ Displaystyle 0 \ równoważnik u \ równoważnik {\ sqrt {p \ lewo ({\ Frac {v} {u}} \ prawo)}}}$ ${\ Displaystyle 0 \ równoważnik v \ równoważnik - {\ Frac {u} {\ lambda}} \ ln {\ Frac {u ^ {2}} {\ lambda}}}$ , co pozwala nam wykreślić kształt zbioru (patrz wykres).

Ta nierówność pozwala nam również wyznaczyć prostokątną obwiednię, $}$ której jest $\ displaystyle {\ tylda {A}} _ {f, 1$ . Rzeczywiście, z ${\ Displaystyle g (u) = - {\ Frac {u} {\ lambda}} \ ln {\ Frac {u ^ {2}} {\ lambda }}}$ , mamy ${\ Displaystyle g \ lewo ({\ sqrt {\ lambda}} \ prawo) = 0}$ i ${\ Displaystyle g'\ lewo ({\ Frac {2} {\ operatorname {e} {\sqrt {\lambda }}}}\right)=0}$ , skąd ${\ Displaystyle {\ tylda {A}} _ {f, 1} = \ lewo [0, {\ sqrt {\ lambda}} \ prawo] \ razy \ lewo [0, g \ lewo ({\ Frac {2} {\mathrm {e} {\sqrt {\lambda}}}}\right)\right]}$ .

Stąd $_$ _ ${\ Displaystyle V \ sim \ operatorname {Unif} \ lewo (0, g \ lewo ({\ Frac {2} {\ operatorname {e} {\ sqrt {\lambda }}}}\right)\right)}$ aż do $}}}}}}} ,$ równoważnik {\ sqrt {\ lambda \, \ operatorname {e} ^ {- \ lambda {\ Frac { $rozkład$ wykładniczy.

Rozkład normalny mieszaniny przed i po zmianie zmiennych metodą ilorazową równomierności. U góry : wykres rozkładu mieszaniny

.

.

: zbiór dla dwóch

różnych

Linie ciągłe na górze przedstawiają detransformację ramek ograniczających na dole. Linie ciągłe na dole

przedstawiają

położenie różnych wartości zestawie.

Mieszanka rozkładów normalnych

Rozważmy mieszaninę dwóch rozkładów normalnych . ${\ displaystyle {\ mathcal {D}} = 0,6 \, N (\ mu =-1,\sigma =2)+0,4\,N(\mu =3,\sigma =1)}$ . Aby zastosować metodę stosunku mundurów, przy danym ${\ displaystyle r}$ $}$ najpierw określić granice prostokątnej ramki ograniczającej otaczającej zbiór. ${A}} _ {f,$ tylde . Można to zrobić numerycznie, obliczając minimum i maksimum z ${\ Displaystyle u (x) = f (x) ^ {\ Frac {1} {1+r} }}$ i ${\ Displaystyle v (x) = x \, f (x) ^ {\ Frac {r} {1+r}}}$ na siatce wartości ${\ displaystyle x }$ . Następnie można narysować jednolite próbki $tylko$ mieszczą się w ustaw i zwróć je jako $} {u ^ {r}}}}$ v $\ displaystyle A_ {f, r}}$