Transformacja Mojette

Transformacja Mojette to aplikacja geometrii dyskretnej . Mówiąc dokładniej, jest to dyskretna i dokładna wersja transformacji Radona , a więc operator projekcji.

Laboratorium IRCCyN - UMR CNRS 6597 w Nantes we Francji rozwija go od 1994 roku.

Pierwszą cechą transformacji Molette jest używanie tylko dodawania i odejmowania. Drugą cechą charakterystyczną jest to, że Transformacja Molette jest zbędna, rozkładając początkowe informacje geometryczne na kilka projekcji.

Ta transformacja wykorzystuje dyskretną geometrię w celu przesłania informacji na dyskretną geometryczną podporę. To wsparcie jest następnie projektowane przez operatora Mojette wzdłuż dyskretnych kierunków. Gdy dostępna jest wystarczająca liczba prognoz, można zrekonstruować początkowe informacje.

Transformacja Mojette została już wykorzystana w wielu dziedzinach aplikacji:

Tomografia medyczna
Transfer pakietów sieciowych
Rozproszone przechowywanie na dyskach lub w sieciach
Schematy pobierania odcisków palców i kryptografii obrazu

Historia

Po roku badań pierwsza komunikacja wprowadzająca Transformację Mojette odbyła się w maju 1995 roku podczas pierwszej edycji Krajowego Kongresu CORESA CCITT Rennes. Wielu innych będzie podążać za nim przez 18 lat istnienia. W 2011 roku książka The Mojette Transform: Theory and Applications at ISTE-Wiley została dobrze przyjęta przez społeczność naukową. Całe to wsparcie zachęciło zespół badawczy IRCCyN do kontynuowania badań na ten temat.

Jeanpierre Guédon, profesor i wynalazca transformacji, nazwał ją: „Mojette Transform”. Słowo „Mojette” pochodzi od nazwy białej fasoli w Vendee, pierwotnie zapisywanej jako „Moghette” lub „Mojhette”. W wielu krajach fasola jest podstawowym narzędziem edukacyjnym reprezentującym dokładną jednostkę, która wizualnie uczy dodawania i odejmowania. Dlatego wybór nazwy „Mojette” służy podkreśleniu faktu, że transformacja używa tylko dokładnych jednostek w dodawaniu i odejmowaniu.

W Vendee jest stare francuskie powiedzenie: „liczyć swoje mojettes”, co oznacza umieć liczyć swoje pieniądze. To zdumiewające, że w świecie anglojęzycznym słowo „licznik fasoli” odnosi się do niegorliwego urzędnika dokonującego dodatków. Stare angielskie powiedzenie mówi „on wie, ile fasoli daje pięć”, co oznacza: „on zna się na rzeczy”.

Pierwotnym celem transformacji Molette było stworzenie dyskretnego narzędzia do podziału płaszczyzny Fouriera na sektory kątowe i promieniowe. Pierwszą próbą zastosowania było psychowizualne kodowanie obrazu, odtwarzające kanał wzrokowy człowieka. Jednak nigdy nie został zrealizowany.

Matematyka

„Surowa” transformacja Definicja Mojette jest następująca:

{\ Displaystyle proj (b, p, q) = \ suma _ {k} ^{}\suma _{l}^{}f(k,l)\Delta (b+kq-pl)}

${\ Displaystyle \ Delta (b) = 1}$	${\ styl wyświetlania, jeśli \, \ b = 0}$
${\ Displaystyle \ Delta (b) = 0}$	${\ Displaystyle inaczej}$

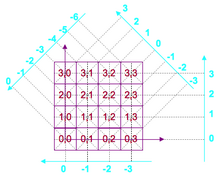
Poniższy rysunek 1 pomaga wyjaśnić „surową” transformację Mojette.

Rysunek 1: Siatka 4x4 z 16 pikselami, 4 projekcjami i 22 pojemnikami

Zaczynamy od funkcji f reprezentowanej przez 16 pikseli od p1 do p16. Możliwe wartości funkcji w punkcie (k, l) różnią się w zależności od zastosowania. Może to być wartość binarna 0 lub 1, której często używa do odróżnienia obiektu od tła. Może to być wartość trójskładnikowa, jak w grze Molette. Może to być również skończony zbiór liczb całkowitych o wartości od 0 do (n-1), lub częściej przyjmujemy zbiór liczności równy potędze 2 lub liczbie pierwszej. Ale mogą to być liczby całkowite i rzeczywiste z nieskończoną liczbą możliwości, mimo że ten pomysł nigdy nie był używany.

Z indeksem „k” jako „kolumna” i „l” jako „linia”, definiujemy kartezjański układ współrzędnych. Ale tutaj będziemy potrzebować tylko współrzędnych całkowitych. Na rysunku 2 arbitralnie wybraliśmy lewy dolny punkt jako początek (0,0) i kierunek dwóch osi. Współrzędne każdego piksela zaznaczono na czerwono na rysunku 2.

Rysunek 2: Znak siatki 4x4 i występy

W przypadku rzutów układ współrzędnych pochodzi z układu siatki. Rzeczywiście spełnia dwa wymagania: 1) Piksel (0,0) jest zawsze rzutowany na punkt 0 rzutu (jest to konsekwencja liniowości operatora Mojette) 2) Kierunek rzutu jest ustalony „przeciwnie do ruchu wskazówek zegara” jak w trygonometrii przy przechodzeniu od 0 ° do 180 °.

W sumie daje to koniecznie pozycje pojemników, takie jak zaznaczone na niebiesko na rysunku 2. Wróćmy do wzoru (1): czerwone kropki odpowiadają indeksowi (k, l), a niebieskie kropki indeksowi B. Jedynymi elementami, które pozostały do wyjaśnienia, są wartości (p, q).

Te dwie wartości (p, q) są dokładnie tymi, które charakteryzują transformację Mojette. Określają kąt projekcji. Rycina 3 pokazuje kolorowe strzałki odpowiadające kodowi koloru projekcji oznaczonej przez (p, q). Dla kąta 90° projekcja jest pokazana poniżej siatki dla wygody, ale kierunek jest skierowany w górę. Tabela 1 pokazuje zgodność między kątami w stopniach a wartościami p i q.

Rysunek 3: Rzuty kierunku (p, q) siatki 4x4

0°	p=1	q=0	b=0
45°	p=1	q=1	b+kl=0
90°	p=0	q=1	b+k=0
135°	p=-1	q=1	b+k+l=0

Tabela 1: Zgodność rzutów kątów z równaniem kierunkowym b + qk - pl = 0

Jedyne ważne kąty Mojette są określone przez następujące zasady:

Kąt jest określony przez kierunek rzutowania w linii i kolumnie
Kierunek składa się z dwóch liczb całkowitych (p, q) gdzie gcd (p, q) = 1
Kąt zawsze mieści się w przedziale od 0 do 180°, co oznacza, że q nigdy nie jest ujemne

Reguły te zapewniają niepowtarzalność zgodności wartości kąta i (p, q). Na przykład kąt 45°, Reguła 2 zabrania definiowania par kątów (2,2) lub (3,3), a Reguła 3 zakazuje używania (-2, -2) i (-1, -1). Tylko kąt (p = 1, q = 1) spełnia trzy reguły.

Aplikacje i osiągnięcia

Dysk lub sieć rozproszonego magazynu

Najważniejszym obszarem zastosowań wykorzystującym „Mojette Transform” jest rozproszona pamięć masowa. W szczególności ta metoda jest używana w RozoFS , rozproszonym systemie plików typu open source . W tej aplikacji „Mojette Transform” jest używany jako kod kasowania w celu zapewnienia niezawodności, przy jednoczesnym znacznym zmniejszeniu całkowitej ilości przechowywanych danych w porównaniu z klasycznymi technikami, takimi jak replikacja (zwykle o współczynnik 2). W ten sposób znacznie obniża koszt klastra pamięci masowej, na przykład pod względem sprzętu, konserwacji lub zużycia energii.

W 2010 roku Pierre Evenou, inżynier naukowy zespołu IVC IRCCyN laboratory, postanowił stworzyć za pomocą tej aplikacji start-up Fizians (obecnie Rozo Systems). Start-up oferuje rozwiązania storage w chmurze obliczeniowej, wirtualizacji, serwerach storage, serwerach plików, backupie i archiwizacji.

Przesyłanie pakietów sieciowych

Dzięki redundancji transformacji przesyłane pakiety mogą być fragmentowane bez strat. Dodatkowo fakt stosowania wyłącznie dodawania i odejmowania zwiększa szybkość przesyłania informacji. Wreszcie informacji nie da się zrekonstruować bez początkowego kąta projekcji, więc zapewnia to również bezpieczeństwo danych.

Ta aplikacja została wybrana przez firmę Thales Cholet do jej sieci ad hoc (wykorzystującej sieć bezprzewodową i terminale do przesyłania wiadomości między nimi) w celu zabezpieczenia informacji i ma wiele ścieżek między źródłem a miejscem docelowym. W 2002 roku start-up PIBI wykorzystał tę technologię do świadczenia bezpiecznych usług płatności internetowych.

Tomografia medyczna

W dziedzinie obrazowania medycznego właściwości „Transform Mojette” tworzą bezpośrednie mapowanie i rozwiązują problem brakującego klina. Jednak akwizycja obrazu za pomocą transformacji Molette nie została jeszcze opracowana. Problem uzyskiwania dokładnych wartości „Mojette” przy użyciu przybliżonej akwizycji danych został zbadany, ale musi być kontynuowany. Poza tym post-processing obrazów medycznych ma się dobrze, ponieważ akwizycja danych jest już zakończona.

Wyniki te wykorzystuje firma Keosys w 2001 roku wraz z Jerome Fortineau oraz firma Qualiformed utworzona w 2006 roku przez Stephena Beaumonta. Prof. Guédon i laboratorium IRCCyN byli mocno zaangażowani w tworzenie tych dwóch firm. Firmy sfinansowały już kilku doktorantów i uczestniczyły w projektach badawczych w celu dalszego rozwoju aplikacji w tomografii medycznej. Wyniki doprowadziły do zastosowania patentów i wdrożeń na swoich urządzeniach do przetwarzania obrazu.

Znak wodny i szyfrowanie obrazu

Kryptografia i znaki wodne były również częścią badań prowadzonych w laboratorium IRCCyN. Dostarcza rozwiązania w zakresie bezpieczeństwa i uwierzytelniania.

W kryptografii niestabilność przekształconego Mojette zabezpiecza dane. Fakt, że transformacja jest dokładna, szyfruje informacje i nie dopuszcza żadnych odchyleń, nawet minimalnych. W przypadku znaku wodnego transformacja jest bardzo skuteczna w pobieraniu odcisków palców. Wstawiając znaki „Mojette Transform” do obrazów, można uwierzytelniać dokumenty przy użyciu tych samych właściwości, co w kryptografii.

Bibliografia

Jeanpierre Guédon, N. Normand, B. Parrein i C. Pouliquen, „Rozproszona transmisja i przechowywanie obrazu w systemie internetowym”, w ACIDCA, 2000, s. 164–169.
B. Parrein, N. Normand i J. Guédon, „Kodowanie wielu opisów przy użyciu dokładnej dyskretnej transformacji Radona”, w IEEE Data Compression Conference, 2001, s. 508.
J. Guédon, N. Normand, P. Verbert, B. Parrein, F. Autrusseau, „Równoważenie obciążenia i skalowalna dystrybucja multimediów przy użyciu transformacji Mojette” w Internet Multimedia Management Systems II, ITCOM, 2001, s. 226–234 .
J. Guédon, B. Parrein, N. Normand, „Internetowy rozproszony system informacji o obrazach”, Zintegrowana inżynieria wspomagana komputerowo, tom. 8, nie. 3, s. 205–214, wrzesień 2008.
B. Parrein, „Description multiple de l'information par transformer Mojette”, Université de Nantes, 2008.
F. Autrusseau i J. Guédon, „Znak wodny obrazu w celu ochrony praw autorskich i ukrywania danych za pomocą transformacji Molette”, w: Bezpieczeństwo i znakowanie wodne treści multimedialnych IV, 2002, s. 378–386.
F. Autrusseau i J. Guédon, „Znaki wodne obrazu w domenie Fouriera przy użyciu transformacji Molette”, w Digital Signal Processing, 2002, s. 725–728.
F. Autrusseau, „Modélisation Psychovisuelle pour le tatouage des images”, Université de Nantes, 2011.
F. Autrusseau i J. Guédon, „Wspólny algorytm wielokrotnego szyfrowania obrazu”, w: International Conference on Image Processing, 2003, s. 269–272.
J. Guédon, N. Normand i B. Parrein, „Multimedialny transport pakietowy: wiele warstw czy opisy?”, w IEEE Packet Video Workshop, 2003, s. 7 str.
B. Parrein, N. Normand i J. Guédon, „Multimedialne kody korygujące błędy przekazywania dla bezprzewodowej sieci LAN”, Annales des Télécommunications, tom. 58, nr. 3–4, s. 448–463, lipiec 2008.
F. Autrusseau i J. Guédon, „Chiffrement Mojette d'images médicales”, Ingénierie des Systèmes d'Information (ISI), tom. 8, nie. 1, s. 113–134, luty 2008.
O. Déforges, M. Babel, N. Normand, B. Parrein, J. Ronsin, J. Guédon i L. Bédat, „Le LAR aux Mojettes” w CORESA 04 - Compression et REprésentation des Signaux Audiovisuels, 2004, s. 165–168.
P. Verbert, V. Ricordel, J. Guédon i P. Verbert, „Analiza projekcji transformacji mojette dla efektywnego kodowania”, w Workshop on Image Analysis for Multimedia Interactive Services (WIAMIS, 2004, s. -.
M. Babel, B. Parrein, O. Déforges, N. Normand, J. Guédon i J. Ronsin, „Bezpieczna i progresywna transmisja skompresowanych obrazów w Internecie: zastosowanie do telemedycyny”, w SPIE 17th Annual Symposium / Electronic Imaging - Obrazowanie w Internecie, 2005, s. 126–136.
J. Guédon i N. Normand, „Transformacja Mojette: pierwsze dziesięć lat”, w: Discrete Geometry for Computer Imagery, 2005, tom. 3429, s. 79–91.
M. Servières, N. Normand, J. Guédon i Y. Bizais, „Transformacja Mojette: Discrete Angles for Tomography”, w Discrete Tomography and its Applications, 2005, tom. 20, s. 587–606.
M. Servieres, „Reconstruction Tomographique Mojette”, Université de Nantes; Ecole centrale de nantes – ECN, 2009.
F. Autrusseau, P. Evenou i T. Hamon, „Bezpieczna rozproszona pamięć masowa oparta na transformacji Mojette”, w Nouvelles Technologies de la répartition, 2006, s. 161–170.
F. Autrusseau, B. Parrein i M. Servieres, „Kompresja bezstratna oparta na dyskretnej i dokładnej transformacji Radona: badanie wstępne”, w Międzynarodowej Konferencji na temat Akustyki, Przetwarzania Mowy i Sygnałów, 2006, s. 425–428.
M. Kalantari, F. Jung, G. Moreau i J. Guédon, „Détection entièrement automatique de points de fuite dans des scènes architectes urbaines”, w: CORESA 2006 COMpression et REprésentation des Signaux Audiovisuels, 2006, s. 41–46.
E. Denis, J. Guédon, S. Beaumont i N. Normand, „Dyskretny i ciągły opis trójwymiarowej sceny do kontroli jakości systemów planowania leczenia radioterapii”, w Medical Imaging, 2006, tom. 6142, str. 187.
M. Servières, N. Normand i J. Guédon, „Metoda interpolacji dla transformacji Mojette”, w Medical Imaging 2006: Physics of Medical Imaging, 2006, tom. 6142, str. 61424I.
N. Normand, A. Kingston i P. Évenou, „Algorytm rekonstrukcji oparty na geometrii dla transformacji Mojette”, w Discrete Geometry for Computer Imagery, 2006, tom. 4245, s. 122–133.
S. Hamma, E. Cizeron, H. Issaka i J. Guédon, „Ocena wydajności reaktywnego i proaktywnego protokołu routingu w sieci ad hoc IEEE 802.11”, w ITCom 06 - sieci nowej generacji i czujników, 2008, s. 638709.
M. Kalantari i M. Kasser, „Implementation of a low-cost photogrametric method for 3d modeling of ceramicfrags”, w XXI International CIPA Symposium, 01-6 października, Ateny, Grecja, 2007, s. FP079.
A. Kingston, S. Colosimo, P. Campisi i F. Autrusseau, „Lossless Image Compression and Selective Encryption using a Discrete Radon Transform”, w International Conference on Image Processing, 2007, s. 465–468.
E. Denis, S. Beaumont, J. Guédon, N. Normand i T. Torfeh, „Automatyczna kontrola jakości cyfrowo zrekonstruowanych obliczeń radiograficznych i porównanie ze standardowymi metodami”, w Medical Imaging 2007: Physics of Medical Imaging, 2007, tom . 6510, str. 65104J.
A. Daurat i N. Normand, „Transformacja i rekonstrukcja par projekcji”, w Géométrie discrète et images numériques, AM David Coeurjolly, wyd. Hermès, 2008, s. 239–251.
N. Normand i J. Guédon, „Aplikacje transformacji Mojette”, w Géométrie discrète et images numériques, AM David Coeurjolly, wyd. Hermès, 2008, s. 337–347.
B. Parrein, F. Boulos, P. Le Callet i J. Guédon, „Priorytetowa transmisja kodowania obrazu i wideo oparta na dyskretnej transformacji Radona”, w IEEE Packet Video 2007, 2007, s. 6 stron.
S. Chandra, I. Svalbe i J. Guédon, „Dokładna, nie-iteracyjna technika inwersji Mojette wykorzystująca duchy”, na 14. międzynarodowej konferencji IAPR na temat dyskretnej geometrii obrazów komputerowych, 2008, s. .
H. Fayad, J. Guédon, I. Svalbe, N. Normand i Y. Bizais, „Tomografy Mojette i FRT”, w Medical Imaging 2008, 2008, tom. 6913, str. -.
M. Kalantari, F. Jung, J. Guédon i N. Paparoditis, „Détection automatique des points de fuite et calcul de leur incertitude à l'aide de la géométrie projective”, w RFIA 2008, 2008, s. 703–712 .
M. Kalantari, F. Jung, N. Paparoditis i J. Guédon, „Solidne i automatyczne wykrywanie punktów zbiegu z ich niepewnością z pojedynczego nieskalibrowanego obrazu, przez ekstrakcję płaszczyzn na jednostce SPHERE”, w ISPRS2008, 2008, s. 203 –208.
H. Fayad, J. Guédon, I. Svalbe, Y. Bizais i N. Normand, „Applying Mojette dyskretny Radon przekształca się w klasyczne dane tomograficzne”, w Medical Imaging, 2008, tom. 6913, str. 69132S.
A. Kingston i F. Autrusseau, „Bezstratna kompresja obrazu poprzez kodowanie predykcyjne dyskretnych projekcji radonu”, „Przetwarzanie sygnału, komunikacja obrazu”, tom. 23, nie. 4, s. 313–324, czerwiec 2008 r.
E. Denis, S. Beaumont, J. Guédon, T. Torfeh, N. Normand i A. Norbert, „Nowe metody automatycznej kontroli jakości narzędzi systemu geometrycznego planowania leczenia w zewnętrznej radioterapii konforemnej”, w Medical Imaging 2008: Physics of Obrazowanie medyczne, 2008, tom. 6913, str. 69133F.
M. Babel, B. Parrein, O. Déforges, N. Normand, J. Guédon i V. Coat, „Wspólne kodowanie kanału źródłowego: zabezpieczona i progresywna transmisja skompresowanych obrazów medycznych w Internecie”, „Computerized Medical Imaging and Graphics” , tom. 32, nie. 4, s. 258–269, kwiecień 2008.
E. Denis, S. Beaumont, J. Guédon, T. Torfeh, N. Normand i N. Ailleres, „Nouvelle méthode automatique de contrôle de qualité des systèmes de planification géométrique des traitements en radiothérapie externe konformationnelle”, w Journées scientifiques de la Société Française de Physique Médicale, 2008, s. Denis.
A. Kingston, B. Parrein i F. Autrusseau, „Nadmiarowa reprezentacja obrazu za pośrednictwem wieloskalowej cyfrowej projekcji radonu”, w International Conf. Przetwarzania Obrazu, 2008, s. 2069.
P. Jia, J. Dong, L. Qi i F. Autrusseau, „Pomiar kierunkowości i oszacowanie oświetlenia powierzchni 3D za pomocą transformacji Mojette”, w 19th International Conference on Pattern Recognition, 2010, s. 1144.
Y. Ben Hdech, J. Guédon i S. Beaumont, „Simulations Monte Carlo d'un faisceau de RX issus d'un accélérateur VARIAN: influence du paramétrage des électrons initiaux”, w Journées Scientifiques de la Société Française de Physique Médicale ( SFPM) 2009: Innovations et bénéfices thérapeutiques: quelles limites?, 2009, s. 1.
Y. Ben Hdech, J. Guédon i S. Beaumont, „Des Objets-Tests Numériques (OTN) anatomiques pour le Contrôle Qualité (CQ) de Systèmes de Planification de Traitement (TPS) en radiothérapie”, w Journées Scientifiques de la Société Française de Physique Médicale (SFPM) 2009: Innovations et bénéfices thérapeutiques: quelles limites?, 2009, s. 1.
M. Kalantari, F. Jung, J. Guédon i N. Paparoditis, „The Five Points Pose Problem: A New and Accurate Solution Adapted to any Geometric Configuration” w The Pacific-Rim Symposium on Image and Video Technology (PSIVT) , 2009, cz. 5414, str. .
D. Coeurjolly i N. Normand, „Dyskretna geometria i projekcje (rozdział 1)” w The Molette Transform: Theory and Applications, jeanpierre Guédon, wyd. iste & wiley, 2009, s. 15 stron.
J. Guédon i N. Normand, „Rekonstrukcyjność z odwrotną transformacją Mojette (rozdział 4)” w The Molette Transform: Theory and Applications, jeanpierre Guédon, wyd. iste & wiley, 2009, s. 15 stron.
J. Guédon i N. Normand, „Bezpośrednia transformacja Mojette (rozdział 3)” w The Mojatte Transform: Theory and Applications, jeanpierre Guédon, wyd. iste & wiley, 2009, s. 23 strony.
A. Kingston i F. Autrusseau, „Kompresja bezstratna (rozdz. 9)” w The Molette transform: Theory and Applications, jeanpierre Guédon, wyd. iste & wiley, 2009, s. 19 stron.
A. Kingston, F. Autrusseau, E. Grall, T. Hamon i B. Parrein, „Bezpieczeństwo oparte na Mojette (rozdział 10)” w The Mojette transform: Theory and Applications, J. Guédon, wyd. iste & wiley, 2009, s. 25 stron.
A. Kingston, F. Autrusseau i B. Parrein, „Wielorozdzielcza transformacja Mojette (rozdz. 6)” w: Transformacja Mojette: Theory and Applications, jeanpierre Guédon, wyd. iste & wiley, 2009, s. 29 stron.
N. Normand, I. Svalbe, P. Evenou i A. Kingston, „Algorytmy odwrotnej transformacji Mojette (rozdział 5)” w: The Mojatte Transform: Theory and Applications, J. Guédon, wyd. iste & wiley, 2009, s. 25 stron.
B. Parrein, F. Boulos, N. Normand i P. Evenou, „Komunikacja, sieci i pamięć masowa (rozdział 7)” w: The Mojette Transform: Theory and Applications, J. Guédon, wyd. iste & wiley, 2009, s. 29 stron.
M. Servières, J. Guédon, N. Normand i Y. Bizais, „Mojette dyskretna tomografia (rozdz. 8)” w The Mojette Transform: Theory and Applications, jeanpierre Guédon, wyd. iste & wiley, 2009, s. 29 stron.
I. Svalbe i J. Guédon, „Dyskretne wersje transformacji Radona (rozdz. 2)” w The Molette Transform: Theory and Applications, jeanpierre Guédon, wyd. iste & wiley, 2009, s. 17 stron.
J. Guédon, Transformacja Mojette. Teoria i zastosowania. ISTE-WILEY, 2009.
S. Beaumont, J. Guédon i Y. Ben Hdech, „Contrôle qualité dosimétrique des systèmes de planification detricement: nouvelle méthode basée sur l'utilisation de PENELOPE et des Objets Tests Numériques anatomiques”, w Journées Scientifiques de la Société Française de Physique Médicale (SFPM), 2010, s. 1.
Y. Ben Hdech, S. Beaumont i J. Guédon, „Développement d'une méthode de Contrôle qualité des Systèmes de Planification des Traitements, utilisés en radiothérapie, au moyen du code Monte-Carlo PENELOPE et des Objets Tests Numériques”, w Journée des doctorants de l'École Doctorale STIM JDOC, 2010, s. 1.
Y. Ben Hdech, S. Beaumont, J. Guédon i T. Torfeh, „Nowa metoda przeprowadzania dozymetrycznej kontroli jakości systemu planowania leczenia przy użyciu PENELOPE Monte-Carlo i anatomicznych cyfrowych obiektów testowych”, w SPIE Medical Imaging 2010, 2010, tom. 7622, str. .
Y. Amouriq, P. Evenou, A. Arlicot, N. Normand i P. Layrolle, „Ocena wzorów kości beleczkowatej na obrazach radiografii dentystycznej: wpływ kości korowej”, w SPIE Medical Imaging, 2010, tom. 7626, str. 76261M.
Y. Amouriq, P. Evenou, A. Arlicot, N. Normand, P. Layrolle, P. Weiss i J. Guédon, „Ocena wzorów kości beleczkowatej na zdjęciach radiograficznych zębów: wpływ kości korowej”, w SPIE Medical Imaging , 2010, s. 10 stron.
A. Arlicot, Y. Amouriq, P. Evenou, N. Normand i J. Guédon, „Algorytm szkieletyzacji pojedynczego skanu: zastosowanie do obrazowania medycznego kości beleczkowej”, w SPIE Medical Imaging, 2010, tom. 7623, str. 762317.
C. Zhang, J. Dong, J. Li i F. Autrusseau, „A New Information Hiding Method for Image Watermarking Based on Molette Transform”, w Second International Symposium on Networking and Network Security, 2010, s. 124–128.
N. Normand, I. Svalbe, B. Parrein i A. Kingston, „Erasure Coding with the Finite Radon Transform”, w: Wireless Communications & Networking Conference, 2010, s. 1–6.
SS Chandra, N. Normand, A. Kingston, J. Guédon i I. Svalbe, „Fast Mojette Transform for Discrete Tomography”, 13 lipca 2012 r.
J. Guédon, C. Liu i J. Guédon, „Scena materiałów 2 i 3 zrekonstruowana z niektórych projekcji liniowych Mojette”, w IEEE IPTA Conference, 2010, s. 6.
Y. Amouriq, J. Guédon, N. Normand, A. Arlicot, Y. Ben Hdech i P. Weiss, „Analiza tekstury kości na zdjęciach radiograficznych zębów: wyniki z kilkoma radiogramami kątowymi na tym samym obszarze zainteresowania”, w SPIE Obrazowanie medyczne 2011: Zastosowania biomedyczne w obrazowaniu molekularnym, strukturalnym i funkcjonalnym, 2012, tom. 7965, str. 796525.
S. Beaumont, T. Torfeh, R. Latreille, Y. Ben Hdech i J. Guédon, „Nowa metoda testowania gantry, kolimatora i kątów obrotu stołu akceleratora liniowego stosowanego w radioterapii”, w SPIE Medical Imaging 2011 , 2011, cz. 7961, s. 796153.
Y. Ben Hdech, S. Beaumont, J. Guédon i C. Sylvain, „Dozymetryczna kontrola jakości systemu planowania leczenia Eclipse przy użyciu cyfrowego obiektu testowego miednicy”, w Medical Imaging 2011: Physics of Medical Imaging, 2011, tom. 7961, s. 79613F.
A. Arlicot, P. Evenou i N. Normand, „Szkieletowanie pojedynczego skanu napędzane odległością sąsiedztwa”, w International Workshop on Combinatorial Image Analysis, IWCIA, 2011, s. 61–72.
A. Arlicot, N. Normand, Y. Amouriq i J. Guédon, „Ekstrakcja struktury kości za pomocą pojedynczego skanowania szkieletu napędzanego odległością” w pierwszych chińsko-francuskich warsztatach na temat współpracy edukacyjnej i badawczej w technologiach informacyjnych i komunikacyjnych, SIFWICT, 2011, s. 2 strony.
Y. Ben Hdech, D. Autret, S. Beaumont i J. Guédon, „Ocena dozymetryczna TPS przy użyciu pakietu 1540-IAEA i symulacji Monte-Carlo”, w ESTRO International Oncology Forum, 2011, s. 1.
C. Liu, J. Guédon, I. Svalbe i Y. Amouriq, „Trójskładnikowe rekonstrukcje i duchy linii Mojette”, w: IWCIA, 2011, s. 11.
C. Liu i J. Guédon, „Ograniczone sceny materialne rekonstruowane przez algorytmy liniowe Mojette”, w konferencji francusko-chińskiej, 2011, s. 2.
J. Dong, L. Su, Y. Zhang, F. Autrusseau i Y. Zhanbin, „Szacowanie kierunku oświetlenia tekstury powierzchni 3D na podstawie aktywnej podstawy i transformacji Mojette”, Journal of Electronic Imaging, tom. 21, nie. 013023, str. 28 stron, kwiecień 2012.
D. Pertin, G. D'Ippolito, N. Normand i B. Parrein, „Spatial Implementation for Erasure Coding by Finite Radon Transform”, w International Symposium on signal, Image, Video and Communication 2012, 2012, s. 1– 4.
P. Bléry, Y. Amouriq, J. Guédon, P. Pilet, N. Normand, N. Durand, F. Espitalier, A. Arlicot, O. Malard i P. Weiss, „Mikroarchitektura napromieniowanej kości: porównanie ze zdrową kości”, w SPIE Medical Imaging, 2012, tom. 8317, str. 831719.
S. Chandra, I. Svalbe, J. Guedon, A. Kingston i N. Normand, „Odzyskiwanie brakujących wycinków dyskretnej transformaty Fouriera za pomocą duchów”, IEEE Transactions on Image Processing, tom. 21, nie. 10, s. 4431–4441, lipiec 2012.
H. Der Sarkissian, Jp. Guédon, P. Tervé, N. Normand i I. Svalbe. (2012). „Ocena degradacji rotacji kątów dyskretnych w obrazowaniu perfuzji mięśnia sercowego”, Doroczny kongres EANM 2012.
C. Liu i J. Guédon, „Znajdowanie wszystkich rozwiązań problemu 3 materiałów”, w materiałach SIFWICT, 2013, s. 6.
B. Recur, H. Der Sarkissian, Jp. Guédon i I.Svalbe, „Tomosynthèse à l'aide de transformées discrètes”, w Proceeding TAIMA 2013
H. Der Sarkissian, B. Recur, N. Normand i Jp. Guédon, „Mojette space Transformations”, w materiałach SWIFCT 2013.
B. Recur, H. Der Sarkissian, M. Servières, N. Normand, Jp. Guédon, „Walidacja rekonstrukcji Mojette z nabytków radonu” w Proceedings of 2013 IEEE International Conference on Image Processing.
H. Der Sarkissian, B. Recur, N. Normand, Jp. Guedon. (2013), „Rotacje w przestrzeni Mojette” w 2013 IEEE International Conference on Image Processing.

Linki zewnętrzne

Media związane z Molette Transform w Wikimedia Commons