Transformacja bezpośrednia-kwadraturowa-zero

„Odq” przekierowuje tutaj. W przypadku innych zastosowań zobacz ODQ (ujednoznacznienie) .

Transformacja bezpośrednia do kwadratury zero ( DQZ lub DQ0 lub DQO , czasami małe litery) lub transformacja zero -bezpośrednia kwadratura ( 0DQ lub ODQ , czasami małe litery) jest tensorem , który obraca ramkę odniesienia trzyelementowego wektora lub trój- macierz o trzech elementach w celu uproszczenia analizy. Transformata DQZ jest iloczynem transformacji Clarke'a i transformacji Parka, po raz pierwszy zaproponowanej w 1929 roku przez Roberta H. Parka .

Transformacja DQZ jest często używana w kontekście elektrotechniki z obwodami trójfazowymi . Transformatę można wykorzystać do obracania ramek odniesienia przebiegów prądu przemiennego , tak aby stały się one sygnałami prądu stałego . Następnie można przeprowadzić uproszczone obliczenia na tych wielkościach prądu stałego przed wykonaniem transformacji odwrotnej w celu odzyskania rzeczywistych wyników trójfazowego prądu przemiennego. Na przykład transformata DQZ jest często stosowana w celu uproszczenia analizy trójfazowych maszyn synchronicznych lub uproszczenia obliczeń do sterowania falownikami trójfazowymi . W analizie trójfazowych maszyn synchronicznych transformacja przenosi trójfazowe wielkości stojana i wirnika do pojedynczego obracającego się układu odniesienia, aby wyeliminować wpływ zmiennych w czasie indukcyjności i przekształcić system w liniowy układ niezmienny w czasie

Wstęp

Transformata DQZ składa się z macierzy transformacji Parka i Clarke'a. Transformata Clarke'a (nazwana na cześć Edith Clarke ) przekształca wektory w układzie odniesienia ABC na układ odniesienia αβγ . Podstawową wartością transformaty Clarke'a jest wyodrębnienie tej części ABC , która jest wspólna dla wszystkich trzech składowych wektora; izoluje składową wspólną (tj. Z ). Niezmienna od potęgi, prawoskrętna, równomiernie skalowana macierz transformacji Clarke'a to

${\ Displaystyle K_ {C} = {\ sqrt {\ Frac {2} {3}}} \ cdot {\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{ \frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1 }{\sqrt {2}}}\end{bmatrix}}}$ .

Aby przekonwertować wektor kolumnowy, do którego odnosi się ABC , na ramkę odniesienia XYZ , wektor musi zostać wstępnie pomnożony przez macierz transformacji Clarke'a:

$\ Displaystyle {\ vec {u}} _ {XYZ} = K_ {C} \ cdot {\ vec {u}} _ {ABC}}$ .

Aby przekonwertować z powrotem wektor kolumnowy, do którego odwołuje się XYZ , do układu odniesienia ABC , wektor musi zostać wstępnie pomnożony przez odwrotną macierz transformacji Clarke'a:

$\ Displaystyle {\ vec {u}} _ {ABC} = K_ {C} ^ {- 1} \ cdot {\ vec {u}} _ {XYZ}}$ .

Transformacja Parka (nazwana na cześć Roberta H. Parka ) konwertuje wektory w ramce odniesienia XYZ na ramkę odniesienia DQZ . Podstawową wartością transformacji Parka jest obracanie układu odniesienia wektora z dowolną częstotliwością. Transformata Parka przesuwa widmo częstotliwości sygnału w taki sposób, że dowolna częstotliwość pojawia się teraz jako „dc”, a stary dc pojawia się jako ujemna dowolna częstotliwość. Macierz transformacji Parka to

${\ Displaystyle K_ {P} = {\ rozpocząć {bmatrix} \ sałata {\ lewo (\ teta \ prawo)}&\sin {\left(\theta \right)}&0\\-\sin {\left(\theta \right)}&\cos {\left(\theta \right)}&0\\0&0&1\ koniec {bmacierz}}}$ ,

gdzie θ jest chwilowym kątem dowolnej częstotliwości ω . Aby przekonwertować XYZ na ramkę odniesienia DQZ , sygnał wektora kolumnowego musi zostać wstępnie pomnożony przez macierz transformacji Parka:

${\ Displaystyle u_ {DQZ} = K_ {P} \ cdot u_ {XYZ}}$ .

Aby przekonwertować z powrotem z wektora odniesienia DQZ na ramkę odniesienia XYZ , sygnał wektora kolumnowego musi zostać wstępnie pomnożony przez odwrotną macierz transformacji Parka:

${\ Displaystyle u_ {XYZ} = K_ {P} ^ {- 1} \ cdot u_ {DQZ}}$ .

Transformacje Clarke'a i Parka razem tworzą transformację DQZ :

$\ Displaystyle K_ {CP} = K_ {P} \ cdot K_ {C}}$

${\ Displaystyle \ do {\ rozpocząć {bmatrix} \ sałata {\ lewo (\ teta \ po prawej)} i \sin {\left(\theta \right)}&0\\-\sin {\left(\theta \right)}&\cos {\left(\theta \right)}&0\\0&0&1\end{bmatrix} }\cdot {\sqrt {\frac {2}{3}}}{\begin{bmatrix}1&{\frac {-1}{2}}&{\frac {-1}{2}}\\0& {\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}}$

${\ Displaystyle \ do {\ sqrt {\frac {2}{3}}}{\begin{bmatrix}\cos {\left(\theta \right)}&\cos {\left(\theta -{\frac {2\pi}}{3 }}\right)}&\cos {\left(\theta +{\frac {2\pi }{3}}\right)}\\-\sin {\left(\theta \right)}&-\ sin {\left(\theta -{\frac {2\pi }{3}}\right)}&-\sin {\left(\theta +{\frac {2\pi }{3}}\right) }\\{\frac {\sqrt {2}}{2}}&{\frac {\sqrt {2}}{2}}&{\frac {\sqrt {2}}{2}}\end{ bmacierz}}}$

Odwrotna transformata to:

${\ Displaystyle K_ {CP} ^ {- 1} = {\ sqrt {\ Frac {2} {3}}} {\ rozpocząć {bmatrix} \ cos {\left(\theta \right)}&-\sin {\left(\theta \right)}&{\frac {\sqrt {2}}{2}}\\\cos {\left(\theta - {\frac {2\pi }{3}}\right)}&-\sin {\left(\theta -{\frac {2\pi }{3}}\right)}&{\frac {\sqrt {2}}{2}}\\\cos {\left(\theta +{\frac {2\pi}}{3}}\right)}&-\sin {\left(\theta +{\frac { 2\pi }{3}}\right)}&{\frac {\sqrt {2}}{2}}\end{bmatrix}}}$

Aby przekonwertować wektor, do którego odnosi się ABC , na ramkę odniesienia DQZ , sygnał wektora kolumnowego musi zostać wstępnie pomnożony przez macierz transformacji DQZ:

${\ Displaystyle u_ {DQZ} = K_ {CP} \ cdot u_ {ABC}}$ .

Aby przekonwertować z powrotem z wektora, do którego odnosi się DQZ , do ramki odniesienia ABC , sygnał wektora kolumnowego musi zostać wstępnie pomnożony przez odwrotną macierz transformacji DQZ:

${\ Displaystyle u_ {ABC} = K_ {CP} ^ {- 1} \ cdot u_ {DQZ}}$ .

Aby lepiej zrozumieć tę transformację, uwzględniono wyprowadzenie transformacji.

Pochodzenie

Wyprowadzenie transformaty Parka

Transformata Parka opiera się na koncepcji iloczynu skalarnego i projekcji wektorów na inne wektory. Najpierw wyobraźmy sobie dwa wektory jednostkowe $u}} _ {D}}$ { \ $kapelusz$ lub osie nowego układu odniesienia z perspektywy starego układu odniesienia) i trzeci, dowolny wektor ${\ displaystyle {\ vec {v}} _ {XY}}$ . Możemy zdefiniować dwa wektory jednostkowe i wektor losowy pod względem ich kartezjańskich w starym układzie odniesienia:

${\ Displaystyle {\ kapelusz {u}} _ {D} = \ sałata {\ lewo (\ teta \ po prawej)}} {\ kapelusz {u}}_ {X}+\sin {\left(\theta \right)}{\kapelusz {u}}_{Y}}$

${\ Displaystyle {\ kapelusz {u}} _ {Q} = - \ sin {\ lewo (\ teta \ po prawej)}} {\ kapelusz {u}} _ {X} + \ cos {\ lewo (\ theta \ prawo)} {\ kapelusz {u}} _ {Y}}$

${\ Displaystyle {\ vec {v}} _ {XY} =v_{X}{\kapelusz {u}}_{X}+v_{Y}{\kapelusz {u}}_{Y}}$ ,

gdzie ${\ Displaystyle {\ hat {u}} _ {X}}$ i ${\ Displaystyle {\ hat {u}} _ {Y}}$ to jednostkowe wektory bazowe starego układu współrzędnych i ${\ Displaystyle \ theta}$$}} _ {X}}$ kąt między ${\ Displaystyle {\ kapelusz$ { u (tj. kąt między dwiema ramkami odniesienia). Rzut dowolnego wektora na każdy z dwóch nowych wektorów jednostkowych implikuje iloczyn skalarny:

${\ Displaystyle v_ {D} = {\ kapelusz {u}} _ {D} \ cdot {\ vec {v}} _ {XY}}$

${\ Displaystyle \ do \ cos {\ lewo (\ teta \ po prawej)} v_ {X} + \ sin {\ lewo (\ teta \ po prawej)} v_ {Y}}$

${\ Displaystyle v_ {Q} = {\ kapelusz {u}} _ {Q} \ cdot {\ vec {v}} _ {XY}}$

${\ Displaystyle \ do - \ sin {\ lewo (\ teta \ po prawej)} v_ {X} + \ cos {\ lewo (\ teta \ po prawej)} v_ {Y}}$ .

Tak więc ${\ displaystyle v_ {D}}$ jest rzutem ${\ displaystyle {\ vec {v}} _ {XY}}$ na u $_ {D}}$$\ displaystyle {\ hat {u}}$$Displaystyle$ jest rzutem ${\ vec {v}} _ {XY}}$ na ${\ displaystyle { \hat {u}}_{Q}}$ oś. Te $}} _ {DQ$ komponenty wektora, razem tworzą nowy wektor ${\ displaystyle v_ {D}}$$v$ Q , oryginalny wektor pod względem nowego układu odniesienia DQ ${\ displaystyle {\ vec {v}} _ {XY}}$

$,$ że powyższy dodatni kąt obrót dowolnego wektora do tyłu po przejściu do nowej ramki odniesienia DQ . Innymi słowy, jego kąt względem nowego układu odniesienia jest mniejszy niż jego kąt względem starego układu odniesienia. Dzieje się tak, ponieważ układ odniesienia, a nie wektor, został obrócony do przodu. W rzeczywistości obrót układu odniesienia do przodu jest identyczny z ujemnym obrotem wektora. Gdyby stary układ odniesienia obracał się do przodu, na przykład w trójfazowych układach elektrycznych, wynikowy wektor DQ pozostaje nieruchomy.

Pojedyncze równanie macierzowe może podsumować powyższą operację:

${\ Displaystyle {\ vec {v}} _ {DQ} = {\ rozpocząć{bmatrix}\cos {\left(\theta \right)}&\sin {\left(\theta \right)}\\-\sin {\left(\theta \right)}&\cos {\left (\theta \right)}\end{bmatrix}}\cdot {\vec {v}}_{XY}}$ .

Ten tensor można rozszerzyć na problemy trójwymiarowe, w których oś, wokół której następuje obrót, pozostaje niezmieniona. W poniższym przykładzie obrót dotyczy Z , ale można było wybrać dowolną oś:

${\ Displaystyle K_ {P} = {\ rozpocząć {bmatrix} \ sałata {\ lewo (\ teta \ prawo)}&\sin {\left(\theta \right)}&0\\-\sin {\left(\theta \right)}&\cos {\left(\theta \right)}&0\\0&0&1\ koniec {bmacierz}}}$ .

Z perspektywy algebry liniowej jest to po prostu obrót zgodnie z ruchem wskazówek zegara wokół osi z i jest matematycznie równoważny wzorom trygonometrycznym różnicy kątów .

Wyprowadzenie transformaty Clarke'a

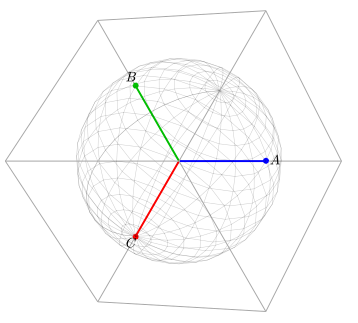
Wektory bazowe jednostek ABC

Rozważmy trójwymiarową przestrzeń z jednostkowymi wektorami bazowymi A , B i C . Kula na poniższym rysunku służy do pokazania skali układu odniesienia dla kontekstu, a ramka służy do przedstawienia kontekstu obrotowego.

Zazwyczaj w elektrotechnice (lub w każdym innym kontekście wykorzystującym systemy trójfazowe) komponenty trójfazowe są pokazane w perspektywie dwuwymiarowej. Jednak biorąc pod uwagę, że trzy fazy mogą zmieniać się niezależnie, są one z definicji prostopadłe do siebie. Oznacza to trójwymiarową perspektywę, jak pokazano na powyższym rysunku. Tak więc perspektywa dwuwymiarowa tak naprawdę pokazuje projekcję trójwymiarowej rzeczywistości na płaszczyznę.

Problemy trójfazowe są zwykle opisywane jako występujące w tej płaszczyźnie. W rzeczywistości problem jest prawdopodobnie problemem zrównoważonej fazy (tj. v _A + v _B + v _C = 0), a wektor wypadkowy

$A} {\ kapelusz {u}} _ {A} + v_ {B }{\kapelusz {u}}_{B}+v_{C}{\kapelusz {u}}_{C}}$

jest zawsze w tej płaszczyźnie.

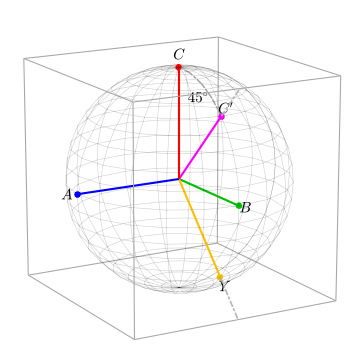
Jednostkowe wektory bazowe AYC'

Aby zbudować transformatę Clarke'a, faktycznie używamy transformacji Parka w dwóch krokach. Naszym celem jest obrócenie C w róg pudełka. W ten sposób obrócona C będzie prostopadła do płaszczyzny wspomnianej perspektywy dwuwymiarowej. Pierwszym krokiem w kierunku zbudowania transformaty Clarke'a jest obrócenie ABC wokół osi A. Tak więc tym razem 1 będzie w pierwszym elemencie transformacji Parku:

${\ Displaystyle K_ {1} = {\ rozpocząć {bmatrix} 1 i 0 i 0 \\0&\cos {\left(-{\frac {\pi }{4}}\right)}&\sin {\left(-{\frac {\pi }{4}}\right)}\\ 0&-\sin {\left(-{\frac {\pi }{4}}\right)}&\cos {\left(-{\frac {\pi }{4}}\right)}\end{ bmatrix}}}$

${\ Displaystyle \ do {\ rozpocząć {bmatrix} 1 & 0 & 0 \\ 0 & {\ Frac {1} {\ sqrt {2}}} & - {\ frac {1}{\sqrt {2}}}\\0&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}} }$

Poniższy rysunek pokazuje, w jaki sposób _{ramka odniesienia} ABC jest obracana do ramki odniesienia AYC' , gdy dowolny wektor jest wstępnie mnożony przez macierz K1 . Osie C' i Y wskazują teraz punkty środkowe krawędzi pudełka, ale wielkość układu odniesienia nie uległa zmianie (tj. kula nie zwiększyła się ani nie zmniejszyła). Wynika to z faktu, że norma tensor K ₁ wynosi 1: || K ₁ || = 1. Oznacza to, że każdy wektor w ABC będzie nadal miał tę samą wielkość po obróceniu do układu odniesienia AYC .

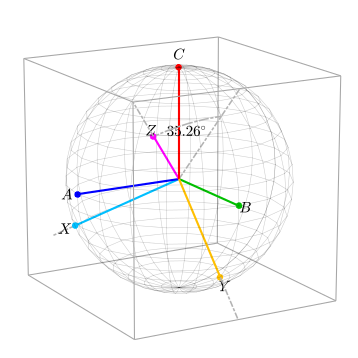
Wektory bazowe jednostek XYZ

Następnie następujący tensor obraca wektor wokół nowej osi Y w kierunku przeciwnym do ruchu wskazówek zegara względem osi Y (kąt został dobrany tak, aby oś C' była skierowana w stronę rogu pudełka.):

${\ Displaystyle K_ {2} = {\ rozpocząć {bmatrix} \ sałata {\ lewo (\ teta \ prawo)}&0&-\sin {\left(\theta \right)}\\0&1&0\\\sin {\left(\theta \right)}&0&\cos {\left(\theta \right)}\end{ bmatrix}}}$

${\ Displaystyle \ teta = \ sałata ^ {- 1} \ lewo ({\ sqrt {\ Frac {2} {3}}} \ prawej) \do 35,26^{\okr}}$ ,

Lub

${\ Displaystyle K_ {2} = {\ rozpocząć {bmatrix} {\ sqrt {\ Frac {2} {3}}} i 0 & - {\ Frac {1 }{\sqrt {3}}}\\0&1&0\\{\frac {1}{\sqrt {3}}}&0&{\sqrt {\frac {2}{3}}}\end{bmatrix}}}$ .

Zauważ, że odległość od środka kuli do środka krawędzi pudełka wynosi √ 2 , ale od środka kuli do rogu pudełka wynosi √ 3 . Stąd wziął się kąt 35,26°. Kąt można obliczyć za pomocą iloczynu skalarnego. $2} {2}} \ prawej)}$${\ Displaystyle {\ vec {m}} = \ lewo (0, {\ Frac {\ sqrt {2}} {2}}, {\ Frac {\ sqrt$ { będzie wektorem jednostkowym w kierunku C ' i niech ${\ Displaystyle {\ vec {n}} = \ lewo ( {\frac {1}{\sqrt {3}}},{\frac {1}{\sqrt {3}}},{\frac {1}{\sqrt {3}}}\right)}$ być wektor jednostkowy w kierunku rogu pudełka w ${\ Displaystyle {\ vec {n}} = \ lewo (1,1,1 \ prawej)}$ . Ponieważ ${\ Displaystyle {\ vec {m}} \ cdot {\ vec {n}} = | {\ vec {m}} || {\ vec {n}} | \ cos \ teta,}$ gdzie ${\ Displaystyle \ theta}$ to kąt między ${\ Displaystyle {\ vec {m}}}$ a ${\ Displaystyle {\ vec {n}},}$ mamy

${\ Displaystyle \ lewo (0, {\ Frac {\ sqrt {2}} {2}}, {\ Frac { \sqrt {2}}{2}}\right)\cdot \left({\frac {1}{\sqrt {3}}},{\frac {1}{\sqrt {3}}},{\ frac {1} {\ sqrt {3}}} \ prawej) = \ sałata \ teta}$

${\ Displaystyle \ sałata \ teta = 0 + {\ frac { \sqrt {2}}{2{\sqrt {3}}}}+{\frac {\sqrt {2}}{2{\sqrt {3}}}}={\sqrt {\frac {2}{ 3}}}}$

${\ Displaystyle \ teta = \ sałata ^ {- 1} \ lewo ({\ sqrt {\ Frac {2} {3}}} \ prawej)}$

${\ Displaystyle \ teta = 35,26 ^ {\ cyrk}.}$

Norma macierzy K ₂ również wynosi 1, więc również nie zmienia wielkości żadnego wektora przemnożonego przez macierz K ₂ .

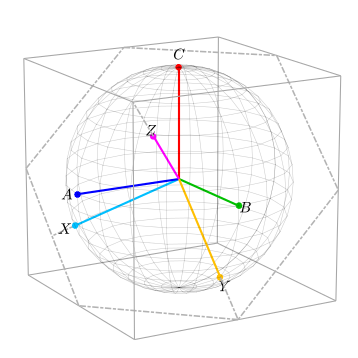
Płaszczyzna zerowa

W tym momencie oś Z jest teraz prostopadła do płaszczyzny, w której można znaleźć dowolny wektor ABC bez składowej trybu wspólnego. Dowolny zrównoważony ABC (wektor bez modu wspólnego) będzie poruszał się po tej płaszczyźnie. Ta płaszczyzna będzie nazywana płaszczyzną zerową i jest pokazana poniżej za pomocą sześciokątnego konturu.

Wektory bazowe X i Y leżą na płaszczyźnie zerowej. Zauważ, że X jest równoległa do rzutu osi A na płaszczyznę zerową. Oś X jest nieco większa niż rzut osi A na płaszczyznę zerową. Jest większy o czynnik √ 3/2 . Dowolny wektor nie zmienił wielkości w wyniku tej konwersji z ABC do układu odniesienia XYZ (tj. sfera nie zmieniła rozmiaru). Odnosi się to do niezmienniczej mocy postaci transformaty Clarke'a. Poniższy rysunek przedstawia wspólną dwuwymiarową perspektywę układów odniesienia ABC i XYZ .

Może się wydawać dziwne, że chociaż wielkość wektora się nie zmieniła, wielkość jego składowych zmieniła się (tj. składowe X i Y są dłuższe niż składowe A , B i C ). Być może można to intuicyjnie zrozumieć, biorąc pod uwagę, że dla wektora bez trybu wspólnego, do wyrażenia którego potrzebne były trzy wartości ( A , B i C ), teraz potrzeba tylko 2 ( składniki X i Y ), ponieważ składnik Z wynosi zero. Dlatego X i Y muszą być większe, aby skompensować.

Kombinacja tensorów

Macierz transformacji Clarke'a niezmiennej pod względem mocy jest kombinacją tensorów K ₁ i K ₂ :

${\ Displaystyle K_ {C} = \ underbrace {\ rozpocząć {bmatrix} {\sqrt {\frac {2}{3}}}&0&-{\frac {1}{\sqrt {3}}}\\0&1&0\\{\frac {1}{\sqrt {3}}}&0& {\sqrt {\frac {2}{3}}}\end{bmatrix}} _{K_{2}}\cdot \underbrace {\begin{bmatrix}1&0&0\\0&{\frac {1}{\sqrt {2}}}&-{\frac {1}{\sqrt {2}}}\\0&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2 }}}\end{bmacierz}} _{K_{1}}}$ ,

Lub

${\ Displaystyle K_ {C} = {\ sqrt {\ Frac {2} {3}}} \ cdot {\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{ \frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1 {\ sqrt {2}}} \ koniec {bmatrix}}}$

${\ Displaystyle \ do {\ rozpocząć {bmatrix}} \frac {2}{\sqrt {6}}}&-{\frac {1}{\sqrt {6}}}&-{\frac {1}{\sqrt {6}}}\\0&{\ frac {1}{\sqrt {2}}}&-{\frac {1}{\sqrt {2}}}\\{\frac {1}{\sqrt {3}}}&{\frac {1 }{\sqrt {3}}}&{\frac {1}{\sqrt {3}}}\end{bmatrix}}}$ .

Zauważ, że po pomnożeniu dolny wiersz macierzy K _C to 1/ √ 3 , a nie 1/3. (Edith Clarke użyła 1/3 w przypadku wariantu mocy). Z nie jest dokładnie średnią składowych A , B i C . Gdyby tylko elementy dolnego rzędu zostały zmienione na 1/3, to kula zostałaby ściśnięta wzdłuż osi Z. Oznacza to, że komponent Z nie miałby takiego samego skalowania jak komponenty X i Y.

Jak napisano powyżej, normą macierzy transformacji Clarke'a jest nadal 1, co oznacza, że ​​obraca ona tylko wektor ABC , ale go nie skaluje. Tego samego nie można powiedzieć o oryginalnej transformacji Clarke'a.

Łatwo sprawdzić (mnożąc macierz), że odwrotnością K _C jest

${\ Displaystyle K_ {C} ^ {- 1} = {\ rozpocząć {bmatrix} {\ Frac {2 }{\sqrt {6}}}&0&{\frac {1}{\sqrt {3}}}\\-{\frac {1}{\sqrt {6}}}&{\frac {1}{\ sqrt {2}}}&{\frac {1}{\sqrt {3}}}\\-{\frac {1}{\sqrt {6}}}&-{\frac {1}{\sqrt { 2}}}&{\frac {1}{\sqrt {3}}}\end{bmatrix}}}$

Forma wariantu mocy

Czasami pożądane jest skalowanie macierzy transformacji Clarke'a tak, aby oś X była rzutem osi A na płaszczyznę zerową. Aby to zrobić, równomiernie stosujemy współczynnik skalowania √ 2/3 i ² √ 1/pierwiastek do składnika zerowego, aby uzyskać macierz transformacji Clarke'a w wariancie potęgowym:

$_ {\ kapelusz {C}} = {\ sqrt {\ frac {2}{3}}}\cdot \underbrace {{\sqrt {\frac {2}{3}}}\cdot {\begin{bmatrix}1&-{\frac {1}{2}}&- {\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1 }{2}}&{\frac {1}{2}}&{\frac {1}{2}}\end{bmatrix}}} _{K_{C}}}$

${\ Displaystyle \ do {\ Frac {2} {3}} {\ rozpocząć {bmatrix} 1 & - {\ Frac {1} {2}} & - {\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1 }{2}}&{\frac {1}{2}}&{\frac {1}{2}}\end{bmatrix}}}$

Lub

${\ Displaystyle K _ {\ kapelusz {C}} = {\ rozpocząć {bmatrix} {\ Frac {2} 3}}&-{\frac {1}{3}}&-{\frac {1}{3}}\\0&{\frac {1}{\sqrt {3}}}&-{\frac { 1}{\sqrt {3}}}\\{\frac {1}{3}}&{\frac {1}{3}}&{\frac {1}{3}}\end{bmatrix}} }$ .

To koniecznie zmniejszy kulę o współczynnik √ 2/3 , jak pokazano poniżej. Zauważ, że ta nowa X jest dokładnie rzutem osi A na płaszczyznę zerową.

W przypadku transformaty Clarke'a w wariancie potęgowym wielkość dowolnego wektora jest mniejsza w układzie odniesienia XYZ niż w układzie odniesienia ABC (normą transformacji jest √ 2/3 ), ale wielkości poszczególnych składowych wektora są taki sam (gdy nie ma trybu wspólnego). Tak więc, jako przykład, sygnał zdefiniowany przez

${\ Displaystyle {\ rozpocząć {bmatrix} A \\ B \\ C \end{bmatrix}}={\begin{bmatrix}\cos {\left(\omega t\right)}\\\cos {\left(\omega t-{\frac {2\pi}}} \right)}\\\cos {\left(\omega t+{\frac {2\pi }{3}}\right)}\end{bmatrix}}}$

staje się w układzie odniesienia XYZ ,

${\ Displaystyle {\ rozpocząć {bmatrix} X \\ Y \\ Z \ koniec {bmatrix}} = {\ rozpocząć { bmatrix}\cos {\lewo(\omega t\prawo)}\\\cos {\lewo(\omega t-{\frac {\pi}}{2}}\prawo)}\\0\koniec{bmatrix} }}$ ,

nowy wektor, którego składowe są tej samej wielkości co oryginalne składowe: 1. W wielu przypadkach jest to korzystna cecha transformaty Clarke'a w wariancie potęgowym.

Transformacja DQZ

Transformacja DQZ wykorzystuje transformatę Clarke'a do konwersji wektorów odniesienia ABC na dwie składowe trybu różnicowego ( tj . Oś Z pod pewnym zadanym kątem. Składowa X staje się składową D , która jest bezpośrednio wyrównana z wektorem obrotu, a składowa Y staje się składową Q , która jest ustawiona pod kątem kwadraturowym do składowej bezpośredniej. Transformacja DQZ jest

$\ Displaystyle K_ {CP} = K_ {P} \ cdot K_ {C}}$

${\ Displaystyle \ do {\ rozpocząć {bmatrix} \ sałata {\ lewo (\ teta \ po prawej)} i \sin {\left(\theta \right)}&0\\-\sin {\left(\theta \right)}&\cos {\left(\theta \right)}&0\\0&0&1\end{bmatrix} }\cdot {\sqrt {\frac {2}{3}}}{\begin{bmatrix}1&{\frac {-1}{2}}&{\frac {-1}{2}}\\0& {\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}}$ .

Implementacja kodu

Ze względu na wydajność obliczeniową sensowne jest oddzielenie transformacji Clarke'a i Parka, a nie łączenie ich w jedną transformację.

Wydajna obliczeniowo implementacja transformaty Clarke'a niezmiennej pod względem mocy jest

            
        
           X  =  (  2  *  ZA  –  B  –  do  )  *  (  1  /  sqrt  (  6  ));  Y  =  (  B  –  C  )  *  (  1  /  sqrt  (  2  ));  Z  =  (  ZA  +  B  +  do  )  *  (  1  /  sqrt  (  3  )); 

podczas gdy jego odwrotność jest

      
        
        
      
       ZA  =  (  1  /  sqrt  (  3  ))  *  Z  ;  B  =  ZA  –  (  1  /  sqrt  (  6  ))  *  X  ;  do  =  B  –  (  1  /  sqrt  (  2  ))  *  Y  ;  B  +=  (  1  /  sqrt  (  2  ))  *  Y  ;  A  +=  (  sqrt  (  2  /  3  ))  *  X  ; 

Wydajna obliczeniowo implementacja transformaty Clarke'a w wariancie mocy

          
        
           X  =  (  2  *  ZA  –  B  –  do  )  *  (  1  /  3  );  Y  =  (  B  –  C  )  *  (  1  /  sqrt  (  3  ));  Z  =  (  ZA  +  B  +  do  )  *  (  1  /  3  ); 

podczas gdy jego odwrotność jest

    
        
        
       ZA  =  X  +  Z  ;  B  =  Z  –  (  1  /  2  )  *  X  ;  do  =  B  –  (  kwadrat  (  3  )  /  2  )  *  Y  ;  B  +=  (  kwadrat  (  3  )  /  2  )  *  Y  ; 

Najwyraźniej stałe współczynniki można było wstępnie obliczyć.

Wydajna obliczeniowo implementacja transformacji Parka to

  
  

    
     co  =  cos  (  teta  );  si  =  grzech  (  teta  );  re  =  co  *  X  +  si  *  Y  ;  Q  =  co  *  Y  -  si  *  X  ; 

podczas gdy jego odwrotność jest

  
  

    
     co  =  cos  (  teta  );  si  =  grzech  (  teta  );  X  =  co  *  re  -  si  *  Q  ;  Y  =  si  *  re  +  co  *  Q  ; 

Sensowne jest obliczenie co i si tylko raz, jeśli mają być użyte zarówno transformaty Parka, jak i odwrotna transformata Parka.

Przykład

W układach elektrycznych bardzo często wartości A , B i C oscylują w taki sposób, że wektor sieci się obraca. W systemie zrównoważonym wektor obraca się wokół osi Z. Bardzo często pomocne jest obrócenie układu odniesienia w taki sposób, aby większość zmian wartości abc spowodowanych tym obrotem została zniwelowana, a wszelkie drobniejsze zmiany stały się bardziej oczywiste. Jest to niezwykle przydatne, ponieważ teraz przekształca system w liniowy system niezmienny w czasie

Transformację DQZ można traktować w kategoriach geometrycznych jako rzut trzech oddzielnych sinusoidalnych wielkości fazowych na dwie osie obracające się z tą samą prędkością kątową, co sinusoidalne wielkości fazowe.

Powyżej pokazano transformację DQZ zastosowaną do stojana maszyny synchronicznej. Istnieją trzy uzwojenia oddzielone od siebie o 120 stopni fizycznych. Prądy trójfazowe są równe co do wielkości i są oddalone od siebie o 120 stopni elektrycznych. Prądy trójfazowe są opóźnione w stosunku do odpowiadających im napięć $o$ . Pokazano $że$ osie DQ obracają się z prędkością kątową równą tej samej prędkości kątowej, co napięcia i prądy fazowe. Oś D $uzwojeniem$ kąt fazy A , wybrane jako odniesienie. Prądy i $są$$_$ .

Porównanie z innymi transformacjami

Metamorfoza Parka

Transformacja pierwotnie zaproponowana przez Park różni się nieco od tej podanej powyżej. W transformacji Parka oś q wyprzedza oś d, qd0, a kąt to kąt między fazą a i osią q, jak podano poniżej: ${\ displaystyle \ theta }$

${\ Displaystyle P = {\ Frac {2} {3}} {\ rozpocząć {bmatrix} \ cos (\ teta) i \ cos (\ teta - {\ Frac {2 \ pi} {3}})&\cos(\theta +{\frac {2\pi }{3}})\\\sin(\theta )&\sin(\theta -{\frac {2\pi }{3 }})&\sin(\theta +{\frac {2\pi }{3}})\\{\frac {1}{2}}&{\frac {1}{2}}&{\frac {1}{2}}\end{bmacierz}}}$

I

${\ Displaystyle P ^ {- 1} = {\ rozpocząć {bmatrix} \ cos (\ teta) i \ sin (\ teta) i 1 \\\ cos (\ teta - {\ Frac {2 \ pi }{3}})&\sin(\theta -{\frac {2\pi }{3}})&1\\\cos(\theta +{\frac {2\pi }{3}})&\ sin(\theta +{\frac {2\pi }{3}})&1\end{bmatrix}}}$

D. Holmes i T. Lipo, Modulacja szerokości impulsu dla przetwornic mocy: zasady i praktyka, Wiley-IEEE Press, 2003 oraz

P. Krause, O. Wasynczuk i S. Sudhoff, Analiza maszyn elektrycznych i systemów napędowych, wyd. 2, Piscataway, NJ: IEEE Press, 2002.

transformacja αβγ

Główny artykuł: transformacja αβγ

Transformacja dqo jest koncepcyjnie podobna do transformacji αβγ . Podczas gdy transformata dqo jest rzutem wielkości fazowych na obracający się dwuosiowy układ odniesienia, transformata αβγ może być traktowana jako rzut wielkości fazowych na nieruchomy dwuosiowy układ odniesienia.

Referencje bezpośrednie

Referencje ogólne

• CJ O'Rourke i in. „Geometryczna interpretacja układów odniesienia i przekształceń: dq0, Clarke i Park”, w IEEE Transactions on Energy Conversion, tom. 34, nie. 4, s. 2070-2083, grudzień 2019 r.
•   J. Lewis Blackburn Symetryczne komponenty do inżynierii systemów zasilania , Marcel Dekker, Nowy Jork (1993). ISBN 0-8247-8767-6
• Zhang i in. Falownik trójfazowy z nogą neutralną z modulacją wektora przestrzennego IEEE APEC '97 Conference Proceedings (1997).
• TAlipo, „Kartezjańskie podejście wektorowe do teorii odniesienia maszyn prądu przemiennego”, Int. Konferencja na temat maszyn elektrycznych, Lozanna, 18–24 września 1984 r.

Zobacz też

• Elementy symetryczne
• transformacja ${\ Displaystyle \ alfa \ beta \ gamma}$
• Sterowanie wektorowe (silnik)