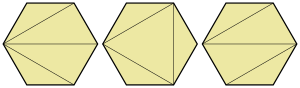
Triangulacja minimalnej wagi

Trzy możliwe triangulacje tego samego wielokąta. Centralna triangulacja ma mniejszą wagę (suma obwodów).

W geometrii obliczeniowej i informatyce problem triangulacji minimalnej wagi to problem znalezienia triangulacji o minimalnej całkowitej długości krawędzi . Oznacza to, że wielokąt wejściowy lub wypukła powłoka zbioru punktów wejściowych musi być podzielona na trójkąty, które stykają się krawędzią do krawędzi i wierzchołkiem do wierzchołka, w taki sposób, aby zminimalizować sumę obwodów trójkątów. Problem jest NP-trudny dla danych wejściowych zestawu punktów, ale można je przybliżyć z dowolnym pożądanym stopniem dokładności. W przypadku wejść wielokątnych można go rozwiązać dokładnie w czasie wielomianowym. Minimalna triangulacja wagowa była czasami nazywana triangulacją optymalną .

Historia

Problem triangulacji minimalnej wagi zbioru punktowego został postawiony przez Düppe i Gottschalk (1970) , którzy zasugerowali jego zastosowanie do konstrukcji trójkątnych nieregularnych modeli sieciowych obrysów terenu i zastosowali zachłanną heurystykę do jego przybliżenia. Shamos i Hoey (1975) przypuszczali, że triangulacja minimalnej wagi zawsze pokrywała się z triangulacją Delaunaya , ale zostało to szybko obalone przez Lloyda (1977) i rzeczywiście Kirkpatricka (1980) wykazało, że wagi dwóch triangulacji mogą różnić się o czynnik liniowy.

Problem triangulacji minimalnej wagi stał się znany, gdy Garey i Johnson (1979) umieścili go na liście otwartych problemów w swojej książce o NP-zupełności , a wielu późniejszych autorów opublikowało częściowe wyniki na jego temat. Wreszcie, Mulzer i Rote (2008) wykazali, że jest to NP-trudne, a Remy i Steger (2009) wykazali, że dokładne przybliżenia mogą być konstruowane wydajnie.

Złożoność

Wagę triangulacji zbioru punktów na płaszczyźnie euklidesowej definiuje się jako sumę długości jej krawędzi. Jego wariant decyzyjny polega na rozstrzygnięciu, czy istnieje triangulacja wag mniejszych od danej wagi; Mulzer i Rote (2008) udowodnili, że jest NP -trudny . Ich dowodem jest redukcja z PLANAR-1-IN-3-SAT, szczególny przypadek boolowskiego problemu spełnialności , w którym 3-CNF , którego wykres jest płaski jest akceptowane, gdy ma przypisanie prawdy, które spełnia dokładnie jeden literał w każdej klauzuli . Dowód wykorzystuje złożone gadżety i wymaga pomocy komputera w celu sprawdzenia prawidłowego działania tych gadżetów.

Nie wiadomo, czy problem decyzyjny triangulacji o minimalnej wadze jest NP-zupełny , ponieważ zależy to od znanego problemu otwartego, czy sumę rodników można obliczyć w czasie wielomianowym. Jednak Mulzer i Rote zauważają, że problem jest NP-zupełny, jeśli wagi krawędzi są zaokrąglone do wartości całkowitych.

$.$ być skonstruowana w czasie subwykładniczym za pomocą , który uwzględnia wszystkie możliwe proste separatory cykli punktów w triangulacji , rekurencyjnie znajduje optymalną triangulację po każdej stronie cyklu i wybiera separator cykli prowadzący do najmniejszej całkowitej masy. Całkowity czas dla tej metody wynosi ${\ Displaystyle 2 ^ {O ({\ sqrt {n}} \ log n)}}$ .

Przybliżenie

Kilku autorów udowodniło wyniki odnoszące triangulację minimalnej wagi do innych triangulacji pod względem współczynnika aproksymacji , najgorszego przypadku stosunku całkowitej długości krawędzi alternatywnej triangulacji do całkowitej długości triangulacji minimalnej wagi. $duchu$ wiadomo, że triangulacja Delaunaya ma współczynnik aproksymacji a triangulacja zachłanna (triangulacja utworzona przez dodanie krawędzi w kolejności od najkrótszej do najdłuższej każdy krok, w tym krawędź, gdy nie przecina wcześniejszej krawędzi) ma współczynnik aproksymacji równy ${\ Displaystyle \ Theta ({\ sqrt {n}})}$ . Niemniej jednak, w przypadku losowo rozłożonych zbiorów punktów, zarówno triangulacja Delaunaya, jak i zachłanna mieszczą się w logarytmicznym współczynniku minimalnej wagi.

Wynik twardości Mulzera i Rote implikuje również NP-twardość znalezienia przybliżonego rozwiązania ze względnym błędem przybliżenia co najwyżej O(1/n ² ). Zatem w pełni wielomianowy schemat aproksymacji dla triangulacji minimalnej wagi jest mało prawdopodobny. Możliwy jest jednak quasi-wielomianowy schemat aproksymacji: dla dowolnej stałej ε 0 rozwiązanie o współczynniku aproksymacji 1 + ε można znaleźć w quasi-wielomianowym czasie exp(O((log n ) ⁹ ).

Heurystyka

Ze względu na trudność w znalezieniu dokładnych rozwiązań triangulacji minimalnej wagi, wielu autorów badało heurystyki, które w niektórych przypadkach mogą znaleźć rozwiązanie, chociaż nie można udowodnić, że działają we wszystkich przypadkach. W szczególności wiele z tych badań koncentrowało się na problemie znajdowania zestawów krawędzi, które z pewnością należą do triangulacji o minimalnej masie. Jeśli znaleziony w ten sposób podwykres triangulacji o minimalnej wadze okaże się spójny, to pozostałą nietriangulowaną przestrzeń można postrzegać jako tworzącą prosty wielokąt, a całą triangulację można znaleźć za pomocą programowania dynamicznego znaleźć optymalną triangulację tej wielokątnej przestrzeni. To samo podejście do programowania dynamicznego można również rozszerzyć na przypadek, w którym podgraf ma ograniczoną liczbę połączonych elementów, i to samo podejście polegające na znalezieniu połączonego wykresu, a następnie zastosowaniu programowania dynamicznego w celu wypełnienia wielokątnych luk otaczających krawędzie grafu jako część heurystyki do znajdowania triangulacji o małej wadze, ale nie o minimalnej wadze.

Wykres utworzony przez połączenie dwóch punktów, gdy są one najbliższymi sąsiadami, jest z konieczności podgrafem triangulacji minimalnej wagi. Jednak ten graf wzajemnego najbliższego sąsiada jest pasujący , a zatem nigdy nie jest połączony. Pokrewny kierunek badań znajduje duże podgrafy triangulacji o minimalnej masie przy użyciu β -szkieletów opartych na okręgu , wykresy geometryczne utworzone przez włączenie krawędzi między dwoma punktami u i v , gdy nie istnieje trzeci punkt w tworzący kąt uwv większy niż jakiś parametr θ. Wykazano, że dla wystarczająco małych wartości θ tak utworzony wykres jest podgrafem triangulacji o minimalnej masie. Jednak wybór θ potrzebny, aby zapewnić, że jest mniejszy niż kąt {{{1}}} , dla którego β -szkielet jest zawsze spójny.

Bardziej wyrafinowaną technikę zwaną szkieletem LMT zaproponowali Dickerson i Montague (1996) . Jest tworzony w procesie iteracyjnym, w którym utrzymywane są dwa zestawy krawędzi, zestaw krawędzi, o których wiadomo, że należą do triangulacji o minimalnej wadze, oraz zestaw krawędzi, które są kandydatami do przynależności do niej. Początkowo zestaw znanych krawędzi jest inicjalizowany do otoczki wypukłej wejścia, a wszystkie pozostałe pary wierzchołków tworzą krawędzie kandydujące. Następnie w każdej iteracji procesu konstrukcyjnego krawędzie kandydujące są usuwane, gdy nie ma pary trójkątów utworzonych przez pozostałe krawędzie tworzące czworobok, dla którego kandydująca krawędź jest najkrótszą przekątną, a kandydujące krawędzie są przesuwane do zbioru znanych krawędzi gdy nie ma innej kandydującej krawędzi, która je przecina. Szkielet LMT jest zdefiniowany jako zestaw znanych krawędzi powstałych po tym, jak ten proces przestanie wprowadzać więcej zmian. Gwarantuje, że będzie to podwykres triangulacji o minimalnej wadze, może być konstruowany wydajnie, aw eksperymentach na zbiorach do 200 punktów często był połączony. Jednak wykazano, że średnio dla dużych zbiorów punktowych ma on liniową liczbę połączonych elementów.

Inne heurystyki, które zostały zastosowane do problemu triangulacji minimalnej wagi, obejmują algorytmy genetyczne rozgałęzione i związane oraz algorytmy optymalizacji kolonii mrówek .

Wariacje

Triangulację wielokątów o minimalnej wadze można skonstruować w czasie sześciennym przy użyciu podejścia do programowania dynamicznego , opisanego niezależnie przez Gilberta (1979) i Klincska (1980) . W tej metodzie wierzchołki są numerowane kolejno wokół granicy wielokąta, a dla każdej przekątnej od wierzchołka i do wierzchołka j , która leży w wielokącie, optymalna triangulacja jest obliczana poprzez uwzględnienie wszystkich możliwych trójkątów ijk w wielokącie, dodanie wag optymalnych triangulacji poniżej przekątnych ik i jk oraz wybierając wierzchołek k , który prowadzi do minimalnej masy całkowitej. Oznacza to, że jeśli MWT( i , j ) oznacza wagę triangulacji minimalnej wagi wielokąta poniżej krawędzi ij , to ogólny algorytm wykonuje następujące kroki:

• Dla każdej możliwej wartości i od n − 1 do 1 wykonaj:
  • Dla każdej możliwej wartości j , od i + 1 do n , wykonaj:
    • Jeśli ij jest krawędzią wielokąta, ustaw MWT( i , j ) = długość ( ij )
    • W przeciwnym razie, jeśli ij nie jest wewnętrzną przekątną wielokąta, ustaw MWT( i , j ) = +∞
    • Inaczej ustaw MWT( i , j ) = długość ( ij ) + min _{i < k < j} MWT( i , k ) + MWT( k,j )

Po zakończeniu tej iteracji MWT(1, n ) zapisze całkowitą wagę triangulacji minimalnej wagi. Samą triangulację można uzyskać rekurencyjnie przeszukując tę ​​tablicę, zaczynając od MWT(1, n ), na każdym kroku wybierając trójkąt ijk prowadzący do minimalnej wartości dla MWT( i , j ) i rekurencyjnie przeszukując MWT( i , k ) i MWT( j , k ).

Podobne metody programowania dynamicznego można również dostosować do danych wejściowych zbioru punktów, w których wszystkie oprócz stałej liczby punktów leżą na wypukłym korpusie danych wejściowych , oraz do zbiorów punktów, które leżą na stałej liczbie zagnieżdżonych wielokątów wypukłych lub na stałej liczbie linii żadne dwa z nich nie krzyżują się w wypukłej otoczce.

Możliwe jest również sformułowanie wersji problemów ze zbiorem punktów lub triangulacją wielokątów, w których można dodawać punkty Steinera , dodatkowe wierzchołki, w celu zmniejszenia całkowitej długości krawędzi wynikowych triangulacji. W niektórych przypadkach wynikowa triangulacja może być krótsza niż triangulacja minimalnej wagi nawet o współczynnik liniowy. Możliwe jest przybliżenie minimalnej wagi triangulacji Steinera punktu ustawionego w ramach stałego współczynnika optymalnego, ale stały współczynnik przybliżenia jest duży.

Powiązane problemy, które również zostały zbadane, obejmują konstrukcję pseudotriangulacji o minimalnej wadze i charakterystykę wykresów triangulacji o minimalnej wadze.

Notatki

•   Aichholzer, Oswin; Aurenhammer Franz ; Hackl, Thomas; Speckmann, Bettina (2009), „O pseudotriangulacjach minimalnej wagi”, Computational Geometry Theory and Applications , 42 (6–7): 627–631, doi : 10.1016/j.comgeo.2008.10.002 , MR 2519380 .
• Aichholzer, Oswin; Aurenhammer Franz ; Hainz, Reinhard (1999), „Nowe wyniki na podgrafach MWT”, Information Processing Letters , 69 (5): 215–219, doi : 10.1016 / S0020-0190 (99) 00018-6 .
•   Anagnostou, Eftymios; Corneil, Derek (1993), „Wielomianowe przypadki problemu triangulacji minimalnej wagi”, Computational Geometry. Teoria i zastosowania , 3 (5): 247–259, doi : 10.1016/0925-7721(93)90016-Y , MR 1251594 .
•   Beirouti, Ronald; Snoeyink, Jack (1998), „Implementacje heurystyki LMT dla triangulacji minimalnej wagi”, Proc. 14. Sympozjum ACM na temat geometrii obliczeniowej , s. 96–105, doi : 10.1145/276884.276895 , S2CID 15102126 .
• Bose, Prosenjit ; Devroye, Luc; Evans, William (1996), „Diamenty nie są najlepszym przyjacielem triangulacji o minimalnej wadze”, Proc. 8. kanadyjska konferencja na temat geometrii obliczeniowej (CCCG 1996) (PDF) , s. 68–73 .
•   Capp, Kerry; Julstrom, Bryant A. (1998), „Algorytm genetyczny z kodowaniem wagowym dla problemu triangulacji minimalnej masy”, Proc. ACM Symposium on Applied Computing , Atlanta, Georgia, Stany Zjednoczone, s. 327–331, doi : 10.1145/330560.330833 , S2CID 13589205 , Semantic Scholar .
• Cheng, Siu-Wing; Golin, Mardocheusz; Tsang, J. (1995), „Oczekiwana analiza przypadku β -szkieletów z zastosowaniami do konstrukcji triangulacji o minimalnej masie”, Proc. 7. kanadyjska konferencja na temat geometrii obliczeniowej (CCCG 1995) , s. 279–284 .
• Cheng, Siu-Wing; Katoh, Naoki; Sugai, Manabu (1996), „Badanie szkieletu LMT”, Algorytmy i obliczenia , notatki z wykładów z informatyki, tom. 1178, s. 256–265, doi : 10.1007/BFb0009502 .
• Cheng, Siu-Wing; Xu, Yin-Feng (2001), „Na β -szkielecie jako podgrafie triangulacji minimalnej wagi”, Theoretical Computer Science , 262 (1–2): 459–471, doi : 10.1016 / S0304-3975 (00) 00318 -2 .
•   De Loera, Jesús A .; Rambau, Jörg; Santos, Francisco (2010), „3.2.3 Triangulacje chciwe i minimalnej wagi”, Triangulations: Structures for Algorithms and Applications , Algorytmy i obliczenia w matematyce, tom. 25, Springer, s. 102–107, ISBN 978-3-642-12970-4 .
•   Dickerson, Matthew T .; Montague, Mark H. (1996), „A (zwykle?) Połączony podwykres triangulacji minimalnej wagi”, Proc. 12. Sympozjum ACM na temat geometrii obliczeniowej , s. 204–213, doi : 10.1145/237218.237364 , S2CID 18962760 .
• Duppe, RD; Gottschalk, HJ (1970), "Automatische Interpolation von Isolinien bei willkürlich verteilten Stützpunkten", Allgemeine Vermessungs-Nachrichten , 77 : 423–426 . Cytowane przez Mulzer i Rote (2008) oraz Remy i Steger (2009) .
•   Eppstein, David (1994), „Zbliżanie minimalnej wagi triangulacji Steinera” (PDF) , Discrete and Computational Geometry , 11 (2): 163–191, doi : 10.1007 / BF02574002 , MR 1254088 .
•    Garey, MR ; Johnson, DS (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness , San Francisco, Kalifornia: WH Freeman, Problem OPEN12, s. 288 , ISBN 0-7167-1045-5 , MR 0519066 .
• Gilbert, PD (1979), Nowe wyniki w płaskich triangulacjach , Raport R-850, Urbana, Illinois: Coordinated Science Laboratory, University of Illinois .
• Grantson, M.; Borgelt, C.; Levcopoulos, C. (2005), „Triangulacja minimalnej wagi przez wycinanie trójkątów”, Proc. 16. Międzynarodowe Sympozjum Algorytmów i Obliczeń , s. 984–994 .
•   Gudmundsson, Joachim; Levcopoulos, Christos (2007), „Pseudo-triangulacje o minimalnej wadze”, Computational Geometry Theory and Applications , 38 (3): 139–153, doi : 10.1016/j.comgeo.2007.05.004 , MR 2352529 .
•    Heath, LS; Pemmaraju, SV (1994), „Nowe wyniki dla problemu triangulacji minimalnej wagi” , Algorithmica , 12 (6): 533–552, doi : 10.1007/BF01188718 , MR 1297812 , S2CID 21160664 .
• Hoffmann, M.; Okamoto, Y. (2004), „Problem triangulacji minimalnej wagi z kilkoma punktami wewnętrznymi”, Proc. 1. międzynarodowe warsztaty na temat obliczeń parametrycznych i dokładnych , s. 200–212 .
•     Hu, Shiyan (2010), „Nowy asymetryczny region inkluzji dla triangulacji minimalnej wagi”, Journal of Global Optimization , 46 (1): 63–73, CiteSeerX 10.1.1.377.6164 , doi : 10.1007/s10898-009-9409- z , MR 2566136 , S2CID 869128 .
•   Jahani, M.; Bigham, BS; Askari, A. (2010), „Algorytm kolonii mrówek dla triangulacji minimalnej wagi”, International Conference on Computational Science and Its Applications (ICCSA) , s. 81–85, doi : 10.1109/ICCSA.2010.38 , S2CID 11790811 , Semantic Uczony .
• Keil, J. Mark (1994), „Obliczanie podwykresu triangulacji minimalnej wagi” , Computational Geometry: Theory & Applications , 4 (1): 18–26, doi : 10.1016/0925-7721 (94) 90014-0 .
•   Kirkpatrick, David G. (1980), „Uwaga na temat Delaunaya i optymalnych triangulacji”, Information Processing Letters , 10 (3): 127–128, doi : 10.1016/0020-0190 (80) 90062-9 , MR 0566856 .
•   Klincsek, GT (1980), „Minimalne triangulacje domen wielokątnych”, Annals of Discrete Mathematics , 9 : 121–123, doi : 10.1016 / s0167-5060 (08) 70044-x , ISBN 9780444861115 .
•   Knauer, chrześcijanin; Spillner, Andreas (2006), „Algorytm o stałych parametrach dla problemu triangulacji minimalnej wagi w oparciu o małe separatory grafów”, Koncepcje teorii grafów w informatyce , Notatki z wykładów z informatyki, tom. 4271, Berlin: Springer, s. 49–57, doi : 10.1007/11917496_5 , MR 2290717 .
•   Kyoda, Yoshiaki; Imai, Keiko; Takeuchi, Fumihiko; Tajima, Akira (1997), „Podejście typu branch-and-cut dla triangulacji minimalnej wagi”, Algorytmy i obliczenia (Singapur, 1997) , Notatki z wykładów z informatyki, tom. 1350, Berlin: Springer, s. 384–393, doi : 10.1007/3-540-63890-3_41 , MR 1651067 .
•   Lenhart, William; Liotta, Giuseppe (2002), „Problem ciągliwości dla triangulacji minimalnej wagi”, Theoretical Computer Science , 270 (1–2): 261–286, doi : 10.1016 / S0304-3975 (00) 00383-2 , MR 1871072 .
•   Levcopoulos, Christos (1987), „An Ω (√ n ) dolna granica nieoptymalności zachłannej triangulacji”, Information Processing Letters , 25 (4): 247–251, doi : 10.1016 / 0020-0190 (87) 90170- 0 , MR 0896144 .
•   Levcopoulos, Christos (2008), „Triangulacja minimalnej wagi”, w: Kao, Ming-Yang (red.), Encyklopedia algorytmów , Springer, s. 546–548, ISBN 978-0-387-30770-1 .
•    Levcopoulos, C.; Krznaric, D. (1998), „Quasi-chciwe triangulacje przybliżające triangulację minimalnej wagi” (PDF) , Journal of Algorithms , 27 (2): 303–338, doi : 10.1006 / jagm.1997.0918 , MR 1622398 , S2CID 13991653 .
• Lingas, Andrzej (1986), „Triangulacje Chciwego i Delaunaya nie są złe w przeciętnym przypadku”, Information Processing Letters , 22 (1): 25–31, doi : 10.1016/0020-0190 (86) 90038-4 .
•   Lingas, Andrzej (1987), „Nowa heurystyka dla triangulacji minimalnej wagi”, SIAM Journal on Algebraic and Discrete Methods , 8 (4): 646–658, doi : 10.1137/0608053 , MR 0918066 .
• Lingas, Andrzej (1998), „Algorytmy czasu subwykładniczego dla triangulacji minimalnej wagi i problemów pokrewnych”, Proceedings of the 10th Canadian Conference on Computational Geometry (CCCG'98) .
• Lloyd, E. (1977), „O triangulacjach zbioru punktów na płaszczyźnie”, Proc. 18. sympozjum IEEE na temat podstaw informatyki , s. 228–240 .
•   Manacher, Glenn K.; Zobrist, Albert L. (1979), „Ani chciwa, ani triangulacja Delaunay płaskiego zestawu punktów nie zbliża się do optymalnej triangulacji”, Information Processing Letters , 9 (1): 31–34, doi : 10.1016 / 0020-0190 (79 )90104-2 , MR 0537055 .
•   Meijer, Henk; Rappaport, David (1992), „Obliczanie minimalnej triangulacji wagowej zestawu liniowo uporządkowanych punktów”, Information Processing Letters , 42 (1): 35–38, doi : 10.1016/0020-0190 (92) 90129-J , MR 1160443 .
•   Mulzer, Wolfgang; Rote, Günter (2008), „Triangulacja minimalnej wagi jest NP-twarda”, Journal of the ACM , 55 (2), Artykuł A11, arXiv : cs.CG/0601002 , doi : 10.1145/1346330.1346336 , S2CID 1658062 .
• Pleciony, DA; Hong, J. (1987), „Algorytm triangulacji heurystycznej”, Journal of Algorithms , 8 (3): 405–437, doi : 10.1016/0196-6774 (87) 90020-4 .
•   Qin, Kaihuai; Wang, Wenping; Gong, Minglun (1997), „Algorytm genetyczny dla triangulacji minimalnej wagi”, IEEE International Conference on Evolutionary Computation , s. 541–546, doi : 10.1109/ICEC.1997.592370 , hdl : 10722/45578 , S2CID 18775737 , Semantic Scholar .
•   Remy Jan; Steger, Angelika (2009), „Schemat przybliżenia czasu quasi-wielomianowego dla triangulacji minimalnej wagi”, Journal of the ACM , 56 (3), Artykuł A15, doi : 10.1145/1516512.1516517 , S2CID 1781658 .
• Shamos, MI ; Hoey, DJ (1975), „Problemy z najbliższymi punktami”, Proc. 16. sympozjum IEEE na temat podstaw informatyki (PDF) , s. 151–162 .
• Wang, Cao An; Yang, Boting (2001), „Dolna granica dla β -szkieletu należącego do triangulacji o minimalnej wadze”, Computational Geometry: Theory & Applications , 19 (1): 35–46, doi : 10.1016 / S0925-7721 (01) 00008- 6 .
•   Xu, Yin-Feng (1998), „Triangulacje minimalnej wagi”, Podręcznik optymalizacji kombinatorycznej, tom. 2 , Boston, MA: Kluwer Academic Publishers, s. 617–634, MR 1665412 .
•   Yang, Bo Ting; Xu, Yin Feng; You, Zhao Yong (1994), „Algorytm dekompozycji łańcucha do dowodu właściwości na podstawie triangulacji minimalnej wagi”, w: Du, Ding-Zhu; Zhang, Xiang-Sun (red.), Algorytmy i obliczenia: 5. Międzynarodowe Sympozjum, ISAAC '94, Pekin, PR Chiny, 25–27 sierpnia 1994, Proceedings , Lecture Notes in Computer Science, tom. 834, Berlin: Springer, s. 423–427, doi : 10.1007/3-540-58325-4_207 , MR 1316441 .

Linki zewnętrzne

• Minimalna triangulacja wagi przy użyciu kodu źródłowego LMT Skeleton „