Twierdzenie o maksymalnym przepływie i minimalnym odcięciu

W informatyce i teorii optymalizacji twierdzenie o maksymalnym przepływie i minimalnym cięciu mówi, że w sieci przepływowej maksymalna wielkość przepływu przechodzącego od źródła do ujścia jest równa całkowitej masie krawędzi w minimalnym przecięciu , tj. najmniejszej całkowitej masie krawędzi, których usunięcie spowodowałoby odłączenie źródła od ujścia.

Jest to szczególny przypadek twierdzenia o dualności dla programów liniowych i może być użyty do wyprowadzenia twierdzenia Mengera i twierdzenia Kőniga – Egerváry'ego .

Definicje i stwierdzenie

Twierdzenie zrównuje dwie wielkości: maksymalny przepływ przez sieć i minimalną przepustowość przekroju sieci. Aby sformułować twierdzenie, każde z tych pojęć musi być najpierw zdefiniowane.

Sieć

Sieć składa się z

• skończony graf skierowany N = ( V , E ) , gdzie V oznacza skończony zbiór wierzchołków, a E ⊆ V × V to zbiór skierowanych krawędzi;
• źródło s ∈ V i ujście t ∈ V ; _
• funkcja pojemności , u , przez . _ która $odwzorowaniem$ oznaczonym c _uv lub c ( u , ∈ mi dla _ Reprezentuje maksymalny przepływ, który może przejść przez krawędź.

przepływy

Przepływ przez sieć to mapowanie oznaczone przez ${\ Displaystyle f: E \ do \ mathbb {R} ^ {+}}$ oznaczone przez ${\ displaystyle f_ {uv}}$ lub ${\ displaystyle f (u, v)}$ z zastrzeżeniem następujących dwóch ograniczeń: fa : mi → R + {\ Displaystyle f: E \ do \ mathbb {R} ^ {+}}}

1. Ograniczenie pojemności : dla każdej krawędzi ${\ Displaystyle (u, v) \ in E}$ , ${\ displaystyle f_ {uv} \ równoważnik c_ {uv}.}$
2. Zachowanie przepływów : dla każdego wierzchołka $oprócz$ i $źródła i$${\ Displaystyle \ suma \ nolimits _ {\ {u: (u, v) \ w E \}} f_ {uv} = \ suma \ nolimits _ {\ {w: (v, w) \ w E \}} f_ {vw}.}$ . $ujścia$ ) zachodzi następująca równość:
   

Przepływ można zwizualizować jako fizyczny przepływ płynu przez sieć, zgodnie z kierunkiem każdej krawędzi. Ograniczenie wydajności mówi wtedy, że objętość przepływająca przez każdą krawędź w jednostce czasu jest mniejsza lub równa maksymalnej przepustowości krawędzi, a ograniczenie zachowania mówi, że ilość, która wpływa do każdego wierzchołka, jest równa ilości wypływającej z każdego wierzchołka, z wyjątkiem wierzchołków źródłowych i ujścia.

Wartość przepływu jest określona przez

$\ Displaystyle | f | = \ suma \ nolimits _ {\ {v: (s, v) \ in E \}} f_ {sv} = \ suma \ nolimits _ {\ {v: (v, t) \ in E \}} f_ {vt},}$

gdzie jak powyżej $displaystyle$ źródłem, a ujściem sieci jest $t} .$ W analogii do płynu reprezentuje ilość płynu wpływającego do sieci u źródła. Ze względu na aksjomat zachowania dla przepływów jest to to samo, co ilość przepływu opuszczającego sieć w zlewie.

Problem maksymalnego przepływu dotyczy największego przepływu w danej sieci.

Problem z maksymalnym przepływem. Maksymalizuj ${\ displaystyle | f |}$ , to znaczy skierować jak największy przepływ od ${\ displaystyle s}$ do ${\ displaystyle t}$ .

Cięcia

Druga połowa twierdzenia o maksymalnym przepływie i minimalnym cięciu odnosi się do innego aspektu sieci: zbioru cięć. Przekrój C = ( S , T ) jest takim podziałem V , że s ∈ S i t ∈ T . Oznacza to, że s - t to podział wierzchołków sieci na dwie części, ze źródłem w jednej części i ujściem w drugiej. Zestaw cięcia $_$ _ C to zestaw krawędzi, które łączą źródłową część cięcia z częścią zlewu:

${\ Displaystyle X_ {C}: = \ {(u, v) \ w E \: \ u \ w S, v \ w T \} = (S \ razy T) \ cap E.}$

Tak więc, jeśli wszystkie krawędzie w zbiorze cięć C zostaną usunięte, wówczas żaden dodatni przepływ nie jest możliwy, ponieważ w wynikowym wykresie nie ma ścieżki od źródła do ujścia.

Wydajność cięcia st jest sumą wydajności krawędzi w jego zestawie cięć ,

$(i, j) \ in E} c_ {ij} d_{ij},}$

gdzie ${\ Displaystyle$$i \ w S}$ jot ∈ $}$ , {\ $0}$ w przeciwnym razie re ja jot = 1 {\ Displaystyle d_

Zazwyczaj wykres zawiera wiele cięć, ale często trudniej jest znaleźć cięcia o mniejszych wagach.

Minimalny problem cięcia st. Zminimalizuj c ( S , T ) , to znaczy określ S i T tak, aby przepustowość st cięcia była minimalna.

Główne twierdzenie

W powyższej sytuacji można udowodnić, że wartość dowolnego przepływu przez sieć jest mniejsza lub równa przepustowości dowolnego odcinka , a ponadto istnieje przepływ o wartości maksymalnej i przekrój o minimalnej przepustowości. Główne twierdzenie łączy maksymalną wartość przepływu z minimalną przepustowością sieci.

Twierdzenie o maksymalnym przepływie i minimalnym odcięciu. Maksymalna wartość przepływu st jest równa minimalnej przepustowości dla wszystkich cięć st.

Przykład

Maksymalny przepływ w sieci. Każda krawędź jest oznaczona f/c , gdzie f to przepływ przez krawędź, a c to pojemność krawędzi. Wartość przepływu wynosi 5. Istnieje kilka minimalnych s - t o wydajności 5; jeden to S = { s , p } i T = { o , q , r , t }.

Rysunek po prawej pokazuje przepływ w sieci. Adnotacja liczbowa na każdej strzałce, w postaci f / c , wskazuje przepływ ( f ) i pojemność ( c ) strzałki. Przepływy wychodzące ze źródła sumują się do pięciu (2+3=5), podobnie jak przepływy do zlewu (2+3=5), ustalając, że wartość przepływu wynosi 5.

Jeden przekrój s - t o wartości 5 jest dany przez S = { s , p } i T = { o , q , r , t }. Zdolność krawędzi przecinających to cięcie wynosi 3 i 2, co daje wydajność cięcia 3+2=5. (Strzałka od o do p nie jest brana pod uwagę, ponieważ wskazuje od T z powrotem do S .)

Wartość przepływu jest równa wydajności cięcia, co pokazuje, że przepływ jest przepływem maksymalnym, a cięcie minimalnym.

Zwróć uwagę, że przepływ przez każdą z dwóch strzałek łączących S z T jest pełny; tak jest zawsze: minimalne cięcie stanowi „wąskie gardło” systemu.

Formuła programu liniowego

Problem maksymalnego przepływu i problem minimalnego cięcia można sformułować jako dwa pierwotne i dualne programy liniowe .

	Maksymalny przepływ (pierwotny)	Min-cut (podwójny)
zmienne	${\ Displaystyle f_ {uv}}$${\ Displaystyle \ forall (u, v) \ in E}$ [zmienna na krawędź]	${\ Displaystyle d_ {uv}}$${\ Displaystyle \ forall (u, v) \ in E}$ [zmienna na krawędź] ${\ Displaystyle z_ {v}}$${\ Displaystyle \ forall v \ in V \ setminus \ {s, t \}}$ [zmienna na węzeł nieterminalny]
cel	maksymalizować ${\ Displaystyle \ suma \ nolimits _ {v: (s, v) \ w E} f_ {sv}}$ [maks. całkowity przepływ ze źródła]	zminimalizować ${(u, v) \ in E} c_ {uv} d_ {uv}}$ [min. całkowita pojemność krawędzi w cięciu]
ograniczenia	z zastrzeżeniem ${\ Displaystyle {\ rozpocząć {wyrównane} f_ {uv} i \ równoważnik c_ {uv} & & \ forall (u, v) \ in E \\\ suma _ {u} f_ {uv} - \ suma _{w}f_{vw}&=0&&v\in V\setminus \{s,t\}\end{wyrównane}}}$ [ograniczenie na krawędź i ograniczenie na węzeł niekońcowy]	z zastrzeżeniem $\ Displaystyle {\ rozpocząć {wyrównane} d_ {uv} -z_ {u} + z_ {v} i \ geq 0 i & \ forall (u, v) \ in E, u \ neq s, v \ neq t \\ d_ {sv} +z_{v}&\geq 1&&\forall (s,v)\in E,v\neq t\\d_{ut}-z_{u}&\geq 0&&\forall (u,t)\in E,u\neq s\\d_{st}&\geq 1&&{\text{if }}(s,t)\in E\end{wyrównane}}}$ [ograniczenie na krawędź]
ograniczenia znakowe	${\ Displaystyle {\ rozpocząć {wyrównane} f_ {uv} i \ geq 0 & & \ forall (u, v) \ w E \\\ koniec {wyrównane}}}$	${\ Displaystyle {\ rozpocząć {wyrównane} d_ {uv} i \ geq 0 & & \ forall (u, v) \ in E \\ z_ {v} & \ in \ mathbb {R} && \ forall v \ in V \ setminus \ {s ,t\}\end{wyrównane}}}$

Max-flow LP jest prosty. Podwójny LP jest uzyskiwany przy użyciu algorytmu opisanego w podwójnym programie liniowym : zmienne i ograniczenia znakowe dualnego odpowiadają ograniczeniom pierwotnego, a ograniczenia podwójnego odpowiadają zmiennym i ograniczeniom znakowym pierwotnego. Powstały LP wymaga pewnego wyjaśnienia. Interpretacja zmiennych w LP min-cut jest następująca:

${\ Displaystyle d_ {uv} = {\ rozpocząć {przypadki} 1, & {\ tekst {jeśli}} u \ w S {\ tekst {i}} v \ w T {\ tekst {(krawędź}} uv {\ tekst {jest w cięciu)}} \\ 0, & {\ tekst {inaczej}} \ koniec {przypadki}}} z v$

${\ Displaystyle z_ {v} = {\ rozpocząć {przypadki} 1 i {\ tekst {jeśli}} v \ w S \\ 0 i {\ tekst {inaczej}} \ koniec {przypadków}}}$

Cel minimalizacji sumuje wydajność na wszystkich krawędziach zawartych w cięciu.

Ograniczenia gwarantują, że zmienne rzeczywiście reprezentują legalne cięcie:

• Re $-z_ {u} + z_ {v} \ geq 0}$ (odpowiednik re $\ Displaystyle d_ {uv} \ geq z_ {u} -z_ {v}} )$ gwarantują, że dla węzłów nieterminalnych u, v , jeśli u jest w S i v jest w T , to krawędź ( u , w ) jest liczony w cięciu ( ${\ Displaystyle d_ {uv} \ geq 1}$ ).
• Re $} + z_ {v} \ geq 1}$$jest$ gwarantują że jeśli jest w to krawędź (s, v) liczona w cięciu (ponieważ jest z definicji w S )
• Re ${\ Displaystyle d_ {ut} -z_ {u} \ geq 0}$ odpowiednik $jest$ gwarantują, że jeśli jest w S , krawędź (u, t) cięciu (ponieważ jest z definicji w T ).

Zauważ, że ponieważ jest to problem minimalizacji, nie musimy gwarantować, że krawędź nie jest w cięciu - musimy tylko zagwarantować, że każda krawędź, która powinna być w cięciu, jest sumowana w funkcji celu.

Równość w twierdzeniu o max-flow min-cut wynika z silnego twierdzenia o dualności w programowaniu liniowym , które stwierdza, że ​​jeśli program pierwotny ma rozwiązanie optymalne, x *, to program dualny ma również rozwiązanie optymalne, y *, takie, że optymalne wartości utworzone przez dwa rozwiązania są równe.

Aplikacja

Twierdzenie Cederbauma o maksymalnym przepływie

Zobacz też: Twierdzenie o maksymalnym przepływie Cederbauma

Problem maksymalnego przepływu można sformułować jako maksymalizację prądu elektrycznego przez sieć złożoną z nieliniowych elementów rezystancyjnych. W tym sformułowaniu granica prądu   I _między zaciskami wejściowymi sieci elektrycznej jako napięcia wejściowego $V$ w _podejściach jest wadze zestawu do cięcia o minimalnej masie.

$\ Displaystyle \ lim _ {V _ {\ tekst {w}} \ do \ infty} (I_ {in}) = \ min _ {X_ {C}} \ suma _ {(u, v) \ in X_ {C}} c_ {uv}}$

Uogólnione twierdzenie o maksymalnym przepływie i minimalnym odcięciu

Oprócz przepustowości krawędzi, należy wziąć pod uwagę przepustowość w każdym wierzchołku, to znaczy odwzorowanie przepływ f musi oznaczone przez c ( v ) $spełniać$ że nie   tylko   przepustowości i zachowanie przepływów, ale także ograniczenie

${\ Displaystyle \ forall v \ in V \ setminus \ {s, t \}: \ qquad \ sum \ nolimits _ {\ {u \ in V \ mid (u, v) \ in E \}} f_ {uv} \ równoważnik c (v).}$

Innymi słowy, ilość przepływu przechodzącego przez wierzchołek nie może przekroczyć jego przepustowości. Zdefiniuj przecięcie st jako zbiór wierzchołków i krawędzi takich, że dla dowolnej ścieżki od s do t ścieżka zawiera element przecięcia. W tym przypadku pojemność cięcia jest sumą wydajności każdej krawędzi i wierzchołka w nim.

W tej nowej definicji uogólnione twierdzenie o maksymalnym przepływie i minimalnym cięciu mówi, że maksymalna wartość st przepływu jest równa minimalnej przepustowości st cut w nowym znaczeniu.

Twierdzenie Mengera

Zobacz też: Twierdzenie Mengera

W zadaniu nieskierowanych krawędziowo rozłącznych ścieżek mamy dany graf nieskierowany G = ( V , E ) oraz dwa wierzchołki s i t , i musimy znaleźć maksymalną liczbę krawędziowo rozłącznych ścieżek w G .

Twierdzenie Mengera stwierdza , że ​​maksymalna liczba krawędziowo rozłącznych ścieżek st w grafie nieskierowanym jest równa minimalnej liczbie krawędzi w st-zbiorze przekrojowym.

Kwestia wyboru projektu

Sieciowe sformułowanie problemu wyboru projektu z rozwiązaniem optymalnym

W problemie wyboru projektów jest n projektów i m maszyn. Każdy projekt p _i przynosi dochód r ( pi ₎ , a zakup każdej maszyny q _j kosztuje c ( q _j ) . Każdy projekt wymaga wielu maszyn, a każda maszyna może być współużytkowana przez kilka projektów. Problem polega na określeniu, które projekty i maszyny odpowiednio wybrać i zakupić, aby zysk był jak największy.

Niech P będzie zbiorem niewybranych projektów , a Q zbiorem zakupionych maszyn, wówczas problem można sformułować jako:

${\ Displaystyle \ max \ {g \} = \ suma _ {i} r (p_ {i}) - \ suma _ {p_ {i} \ w P} r (p_ {i}) - \ suma _ {q_ {j} \ w Q} c (q_ {j}).}$

Ponieważ pierwszy termin nie zależy od wyboru P i Q , ten problem maksymalizacji można zamiast tego sformułować jako problem minimalizacji, to znaczy

${\ Displaystyle \ min \ {g' \} = \ suma _ {p_ {i} \ w P} r (p_ {i}) + \ suma _ {q_ {j} \ w Q} c (q_ {j}).}$

r ( pi ₎ odcięcia , konstruując sieć, w której źródło jest podłączone do projektów o przepustowości , a ujście jest połączone maszynami o przepustowości c ( q _j ) . Krawędź ( pi _pi , q _j ) o nieskończonej wymaga _pojemności jest dodawana, jeśli projekt maszyny q _j . St cut-set reprezentuje odpowiednio projekty i maszyny w P i Q. Za pomocą twierdzenia o maksymalnym przepływie i minimalnym odcięciu można rozwiązać problem jako problem maksymalnego przepływu .

Rysunek po prawej przedstawia sformułowanie sieciowe następującego problemu wyboru projektu:

	projekt r ( pi ) _	Maszyna c ( q j )
1	100	200	Projekt 1 wymaga maszyn 1 i 2.
2	200	100	Projekt 2 wymaga maszyny 2.
3	150	50	Projekt 3 wymaga maszyny 3.

Minimalna wydajność cięcia to 250, a suma przychodów każdego projektu to 450; zatem maksymalny zysk g wynosi 450 − 250 = 200, wybierając projekty p ₂ i p ₃ .

Chodzi o to, aby „przepłynąć” zyski każdego projektu przez „rury” jego maszyn. Jeśli nie możemy napełnić rury z maszyny, zwrot z maszyny jest mniejszy niż jej koszt, a algorytm minimalnego cięcia uzna, że ​​taniej będzie odciąć przewagę zysku projektu zamiast krawędzi kosztu maszyny.

Problem z segmentacją obrazu

Zobacz też: Problem z maksymalnym przepływem

Każdy czarny węzeł oznacza piksel.

W problemie segmentacji obrazu jest n pikseli. Każdemu pikselowi i lub _można przypisać wartość pierwszego planu bi _fi wartość tła . Istnieje kara p _ij, jeśli piksele i, j sąsiadują ze sobą i mają różne przypisania. Problem polega na przypisaniu pikseli do pierwszego planu lub tła w taki sposób, aby suma ich wartości pomniejszona o kary była maksymalna.

Niech P będzie zbiorem pikseli przypisanych do pierwszego planu, a Q będzie zbiorem punktów przypisanych do tła, wtedy problem można sformułować jako:

${\ Displaystyle \ max \ {g \} = \ suma _ {i \ w P} f_ {i} + \ suma _ {i \ w Q} b_ {i} - \ suma _ {i \ w P, j \ w Q \ lor j \ w P, i \ w Q} p_ {ij}.}$

Ten problem maksymalizacji można zamiast tego sformułować jako problem minimalizacji, to znaczy

${\ Displaystyle \ min \ {g' \} = \ suma _ {i \ w P, j \ w Q \ lor j \ w P, i \ w Q} p_ {ij}.}$

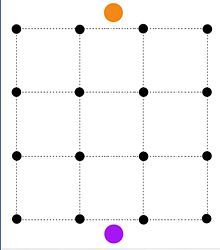
Powyższy problem minimalizacji można sformułować jako problem minimalnego odcięcia, konstruując sieć, w której źródło (węzeł pomarańczowy) jest połączone ze wszystkimi pikselami o pojemności f i , a _ujście (węzeł fioletowy) jest połączone wszystkimi pikselami o pojemności b _i . Dwie krawędzie ( i, j ) oraz ( j, i ) o pojemności p _ij są dodawane między dwoma sąsiednimi pikselami. St cut-set następnie reprezentuje piksele przypisane do pierwszego planu w P i piksele przypisane do tła w Q .

Historia

Relacja z odkrycia twierdzenia została podana przez Forda i Fulkersona w 1962 roku:

„Określenie maksymalnego przepływu w stanie ustalonym z jednego punktu do drugiego w sieci podlegającej ograniczeniom przepustowości na łukach… zostało postawione autorom wiosną 1955 roku przez TE Harrisa, który wraz z generałem FS Rossem (w stanie spoczynku) sformułował uproszczony model przepływu ruchu kolejowego i wskazał ten konkretny problem jako centralny sugerowany przez model. Niedługo potem głównym wynikiem, Twierdzenie 5.1, które nazywamy twierdzeniem o maksymalnym przepływie min-cut, było przypuszczenie ed i ustalono. Od tego czasu pojawiło się wiele dowodów”.

Dowód

Niech G = ( V , E ) będzie siecią (grafem skierowanym), gdzie s i t będą odpowiednio źródłem i ujściem G.

Rozważ przepływ   f   obliczony dla G przez algorytm Forda-Fulkersona . W grafie resztkowym ( G _f ) uzyskanym dla G (po ostatecznym przypisaniu przepływu algorytmem Forda-Fulkersona ) zdefiniuj dwa podzbiory wierzchołków w następujący sposób:

1. A : zbiór wierzchołków osiągalnych z s w G _f
2. A ^c : zbiór pozostałych wierzchołków tj. V − A

Prawo. value( f ) = c ( A , A ^c ) , gdzie wydajność st -cut jest określona przez

${\ Displaystyle c (S, T) = \ suma \ nolimits _ {(u, v) \ w S \ razy T} c_ {uv}}$ .

Teraz wiemy, że dla dowolnego podzbioru wierzchołków A , ${\ Displaystyle value (f) = f_ {out} (A) -f_ {in} (A$ } Dlatego dla value( f ) = c ( A , A ^c ) potrzebujemy:

• Wszystkie krawędzie wychodzące z cięcia muszą być w pełni nasycone .
• Wszystkie krawędzie dochodzące do cięcia muszą mieć zerowy przepływ .

Aby udowodnić powyższe twierdzenie, rozważymy dwa przypadki:

• W G istnieje krawędź wychodząca ${\ Displaystyle (x, y), x \ w A, y \ w A ^ {c}}$ taka, że ​​nie jest nasycona, tj.   fa ( x , y ) < do _xy . Oznacza to, że istnieje przednia krawędź od x do y w G _f , zatem istnieje ścieżka od s do y w G _f , co jest sprzecznością. Stąd każda wychodząca krawędź ( x , y ) jest w pełni nasycona.

• W G istnieje nadchodząca krawędź ${\ Displaystyle (y, x), x \ w A, y \ w A ^ {c}}$ tak, że przenosi pewien niezerowy przepływ, tj.   f ( y , x ) > 0 . Oznacza to, że istnieje tylna krawędź , _od x do y w Gf , _s a zatem istnieje ścieżka od do y w Gf co znowu jest sprzecznością. Stąd każda dochodząca krawędź ( y , x ) musi mieć zerowy przepływ.

Oba powyższe stwierdzenia dowodzą, że uzyskana w wyżej opisany sposób wydajność cięcia jest równa przepływowi uzyskanemu w sieci. Również przepływ został uzyskany za pomocą algorytmu Forda-Fulkersona , więc jest to również maksymalny przepływ sieci.

Ponadto, ponieważ każdy przepływ w sieci jest zawsze mniejszy lub równy przepustowości każdego możliwego odcięcia w sieci, opisane powyżej odcięcie jest również minimalnym odcięciem , które uzyskuje maksymalny przepływ .

Następstwem tego dowodu jest to, że maksymalny przepływ przez dowolny zestaw krawędzi w przecięciu wykresu jest równy minimalnej przepustowości wszystkich poprzednich przekrojów.

Zobacz też

• Przypuszczenie GNRS
• Programowanie liniowe
• Maksymalny przepływ
• Minimalne cięcie
• Sieć przepływu
• Algorytm Edmondsa-Karpa
• Algorytm Forda-Fulkersona
• Przybliżone twierdzenie o maksymalnym przepływie i minimalnym cięciu
• Twierdzenie Mengera

•   Eugeniusza Lawlera (2001). „4.5. Kombinatoryczne implikacje twierdzenia o minimalnym przecięciu maksymalnego przepływu, 4.6. Interpretacja programowania liniowego twierdzenia o minimalnym przecięciu maksymalnego przepływu”. Optymalizacja kombinatoryczna: sieci i matroidy . Dover. s. 117–120. ISBN 0-486-41453-1 .
•   Christos H. Papadimitriou , Kenneth Steiglitz (1998). „6.1 Twierdzenie o maksymalnym przepływie i minimalnym cięciu” . Optymalizacja kombinatoryczna: algorytmy i złożoność . Dover. s. 120–128. ISBN 0-486-40258-4 .
•   Vijay V. Vazirani (2004). „12. Wprowadzenie do dualizmu LP”. Algorytmy aproksymacji . Skoczek. s. 93–100. ISBN 3-540-65367-8 .