Wątkowe drzewo binarne
W informatyce drzewo binarne z wątkami jest wariantem drzewa binarnego , który ułatwia przechodzenie w określonej kolejności (często w tej samej kolejności, która została już zdefiniowana dla drzewa).
Całe drzewo wyszukiwania binarnego można łatwo przeglądać w kolejności klucza głównego, ale mając tylko wskaźnik do węzła , znalezienie następnego węzła może być powolne lub niemożliwe. Na przykład węzły liści z definicji nie mają potomków, więc mając tylko wskaźnik do węzła liścia, nie można dotrzeć do żadnego innego węzła. Drzewo wątkowe dodaje dodatkowe informacje w niektórych lub wszystkich węzłach, dzięki czemu dla dowolnego pojedynczego węzła można szybko znaleźć „następny” węzeł, umożliwiając przechodzenie przez drzewo bez rekurencji i dodatkową pamięć (proporcjonalną do głębokości drzewa), której wymaga rekurencja.
Gwintowanie
„Drzewo binarne jest połączone w wątki , tworząc wszystkie prawe wskaźniki potomne, które normalnie byłyby puste, wskazują na następcę węzła w kolejności ( jeśli istnieje), a wszystkie lewe wskaźniki potomne, które normalnie byłyby puste, wskazują na poprzednika w kolejności węzła".
Zakłada to, że kolejność przechodzenia jest taka sama, jak kolejność przechodzenia przez drzewo. Jednak wskaźniki można zamiast tego (lub dodatkowo) dodawać do węzłów drzewa, zamiast zastępować. połączone listy są również powszechnie nazywane „wątkami” i mogą być używane do umożliwienia przechodzenia w dowolnej pożądanej kolejności. Na przykład drzewo, którego węzły reprezentują informacje o ludziach, może być sortowane według nazwisk, ale ma dodatkowe wątki umożliwiające szybkie przechodzenie w kolejności według daty urodzenia, wagi lub dowolnej innej znanej cechy.
Motywacja
Drzewa, w tym (między innymi) drzewa wyszukiwania binarnego , mogą być używane do przechowywania elementów w określonej kolejności, na przykład wartości niektórych właściwości przechowywanych w każdym węźle, często nazywanych kluczami . Jedną użyteczną operacją na takim drzewie jest przechodzenie : odwiedzanie wszystkich elementów w kolejności klucza.
Prosty rekurencyjny algorytm przechodzenia, który odwiedza każdy węzeł drzewa wyszukiwania binarnego, jest następujący. Załóżmy, że t jest wskaźnikiem do węzła lub nil . „Odwiedzanie” może oznaczać wykonanie dowolnej czynności na węźle t lub jego zawartości.
Trawers algorytmu( t ):
- Dane wejściowe: wskaźnik t do węzła (lub nil )
- Jeśli t = zero , wróć.
- W przeciwnym razie:
- traverse(lewe dziecko( t ))
- odwiedź t
- trawers(prawe dziecko( t ))
Jednym z problemów z tym algorytmem jest to, że ze względu na swoją rekurencję wykorzystuje przestrzeń stosu proporcjonalną do wysokości drzewa. Jeśli drzewo jest dość zrównoważone, odpowiada to O (log n ) dla drzewa zawierającego n elementów. W najgorszym przypadku, gdy drzewo przybiera postać łańcucha , wysokość drzewa wynosi n , więc algorytm zajmuje O ( n ) przestrzeni. Drugi problem polega na tym, że wszystkie przechodzenia muszą zaczynać się od korzenia, gdy węzły mają wskaźniki tylko do swoich dzieci. Powszechne jest posiadanie wskaźnika do określonego węzła, ale to nie wystarczy, aby wrócić do reszty drzewa, chyba że zostaną dodane dodatkowe informacje, takie jak wskaźniki wątków.
W tym podejściu może nie być możliwe stwierdzenie, czy lewy i/lub prawy wskaźnik w danym węźle faktycznie wskazują dzieci, czy też są konsekwencją wątkowania. Jeśli rozróżnienie jest konieczne, wystarczy dodać jeden bit do każdego węzła, aby go zarejestrować.
W podręczniku z 1968 roku Donald Knuth zapytał, czy istnieje nierekurencyjny algorytm do przechodzenia w kolejności, który nie używa stosu i pozostawia niezmodyfikowane drzewo. Jednym z rozwiązań tego problemu jest wątkowanie drzew, przedstawione przez Josepha M. Morrisa w 1979 r. W kolejnym wydaniu z 1969 r. Knuth przypisał reprezentację drzewa wątkowego Perlisowi i Thorntonowi (1960).
Relacja do wskaźników nadrzędnych
Innym sposobem osiągnięcia podobnych celów jest umieszczenie w każdym węźle wskaźnika do węzła nadrzędnego tego węzła. Biorąc to pod uwagę, zawsze można dotrzeć do „następnego” węzła. „właściwe” wskaźniki są nadal puste, gdy nie ma właściwych dzieci. Aby znaleźć „następny” węzeł z węzła, którego prawy wskaźnik jest pusty, przejdź w górę przez wskaźniki „rodzica”, aż dotrzesz do węzła, którego prawy wskaźnik nie jest pusty i nie jest dzieckiem, z którego właśnie wyszedłeś. Ten węzeł jest „następnym” węzłem, a po nim następują jego potomkowie po prawej stronie.
Możliwe jest również odkrycie rodzica węzła z wielowątkowego drzewa binarnego, bez jawnego użycia wskaźników nadrzędnych lub stosu, chociaż jest to wolniejsze. Aby to zobaczyć, rozważmy węzeł k z prawym dzieckiem r . Wtedy lewy wskaźnik r musi być dzieckiem lub wątkiem z powrotem do k . W przypadku, gdy r ma lewe dziecko, to lewe dziecko musi z kolei mieć albo własne lewe dziecko, albo wątek z powrotem do k i tak dalej dla wszystkich kolejnych lewych dzieci. Więc podążając za łańcuchem lewych wskaźników od r , w końcu znajdziemy wątek wskazujący z powrotem na k . Sytuacja jest symetrycznie podobna, gdy q jest lewym dzieckiem p — możemy podążać za prawymi dziećmi q do wątku skierowanego do przodu do p .
W Pythonie :
def parent ( węzeł ): jeśli węzeł jest węzłem . drzewo . root : return Brak x = węzeł y = węzeł podczas True : if is_thread ( y ): p = y . dobrze , jeśli p jest Brak lub p . lewy nie jest węzłem : p
= x podczas gdy nie is_thread ( p . lewy ): p = p . lewo p = p . lewy powrót p elif is_thread ( x ): p = x . w lewo , jeśli p jest Brak lub p . prawy nie jest węzłem : p = y while
nie jest_wątkiem ( p . po prawej ): p = p . prawo p = p . powrót w prawo p x = x . lewo y = y . Prawidłowy
typy
- Pojedynczy wątek: każdy węzeł jest połączony z poprzednikiem lub następcą w kolejności (lewy lub prawy).
- Podwójny wątek: każdy węzeł jest połączony zarówno z poprzednikiem , jak i następnikiem w kolejności (lewy i prawy).
Tablica przechodzenia w kolejności
Wątki są odniesieniami do poprzedników i następników węzła zgodnie z przechodzeniem w kolejności.
Kolejność przechodzenia przez gwintowane drzewo to A,B,C,D,E,F,G,H,I , poprzednikiem E jest D , następnikiem E jest F .
Przykład
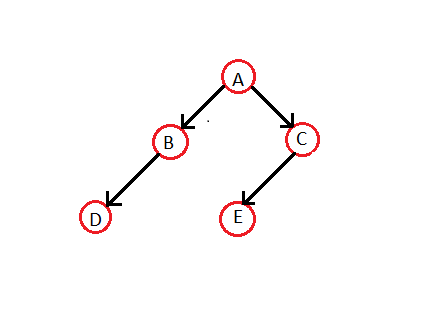
Zróbmy drzewo Threaded Binary z normalnego drzewa binarnego:
Przechodzenie w kolejności dla powyższego drzewa to — DBAE C. Tak więc odpowiednie drzewo wątków binarnych będzie --
Zerowe linki
W m -drożnym drzewie binarnym z n węzłami jest n × m − ( n −1) pustych łączy.