Ważony problem spełnienia ograniczeń

W badaniach nad sztuczną inteligencją i operacjami ważony problem spełnienia ograniczeń ( WCSP ) jest uogólnieniem problemu spełnienia ograniczeń (CSP), w którym niektóre ograniczenia mogą zostać naruszone (zgodnie ze stopniem naruszenia) i w którym preferencje wśród rozwiązań można wyrazić. Uogólnienie to umożliwia przedstawienie większej liczby rzeczywistych problemów, w szczególności tych, które są nadmiernie ograniczone (nie można znaleźć rozwiązania bez naruszenia przynajmniej jednego ograniczenia) lub takich, w których chcemy znaleźć rozwiązanie o minimalnym koszcie (zgodnie z funkcja kosztu ) wśród wielu możliwych rozwiązań.

Definicja formalna

Sieć z ograniczeniami ważonymi (WCN), znana również jako sieć funkcji kosztu (CFN), jest trójką $,$ $k \ rangle}$ { \ dyskretnych zmiennych $}$ skończonym zbiorem miękkich ograniczeń i $jest$ albo naturalną liczbą całkowitą, albo $∞$ .

$uporządkowany$ ograniczenie $l(S)}$ zestaw zmiennych, zwany jego zakresem, i jest definiowany jako funkcja $z$ $\$ do ${\ Displaystyle \ langle 0, ..., k \ rangle}$ gdzie ${\ Displaystyle l (S)}$ zbiorem możliwych instancji ${\ displaystyle S}$ . Kiedy podana jest instancja ${\ Displaystyle I \ w l (S)}$ koszt ${\ Displaystyle k}$ , tj. ${\ Displaystyle c_ {S} (I) =k}$ , mówi się, że jest to zabronione. W przeciwnym razie jest to dozwolone z odpowiednim kosztem (0 jest całkowicie zadowalające).

$określonej podklasie$ ${\ Displaystyle \ forall \ alfa, \ beta \ in \ langle 0, ..., k \ rangle, \ alfa \ oplus \ beta =$ ), koszty są łączone z określonym operatorem zdefiniowanym jako: . Częściowa odwrotność ${\ Displaystyle \ oplus}$ $jest$ zdefiniowana : if ${\ Displaystyle 0 \ równoważnik \ beta \ równoważnik \ alfa <k$ } ${\ Displaystyle \ alfa \ ominus \ beta = \ alfa - \ beta}$ i jeśli ${\ Displaystyle 0 \ równoważnik \ beta <k}$ , ${\ Displaystyle k \ ominus \ beta = k}$ .

Bez utraty ogólności, istnienie ograniczenia zerowego $\ pusty zbiór$ ${\ displaystyle x} .$ również obecność ograniczenia jednoargumentowego dla każdej zmiennej $}}$ zakłada się

$X)}$ pełnej instancji jest ograniczoną sumą kosztu dla $I \$ $\ Displaystyle$ w l wszystkie miękkie ograniczenia $\ Displaystyle c _$ , w tym koszt zerowy $pusty zestaw}}$ koszty jednoargumentowe dla zmiennych w ${\ displaystyle I}$ ${\ Displaystyle X}$ .

Biorąc pod uwagę WCN/CFN, typowym (NP-trudnym) zadaniem WCSP jest znalezienie kompletnej instancji przy minimalnym koszcie. Można zdefiniować inne zadania w pokrewnej dziedzinie modelu graficznego .

Rozdzielczość binarnych/potrójnych WCSP

Podejście z operacjami transferu kosztów

Konsystencja węzła (NC) i spójność łuku (AC), wprowadzone dla problemu spełnienia ograniczeń (CSP), zostały później zbadane w kontekście WCSP. Ponadto zaproponowano kilka konsystencji dotyczących najlepszej postaci spójności łuku: spójność pełnego łuku kierunkowego (FDAC) , spójność łuku kierunkowego egzystencjalnego (EDAC) , spójność łuku wirtualnego (VAC) i spójność optymalnego łuku miękkiego (OSAC) .

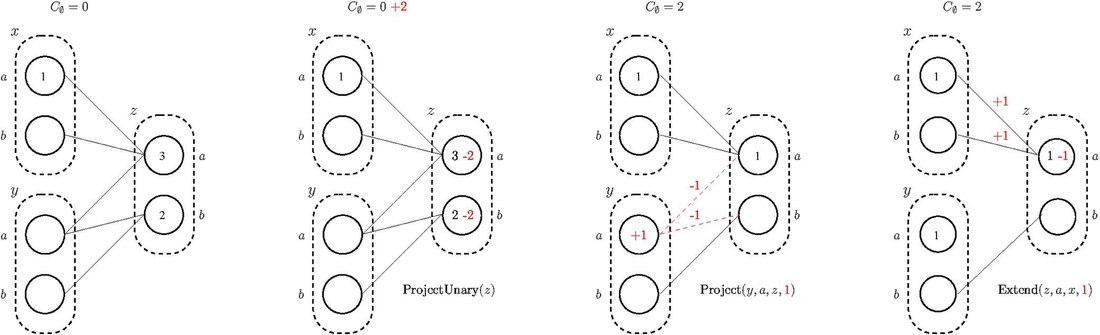
Algorytmy wymuszające takie właściwości są oparte na transformacjach zachowujących równoważność (EPT), które pozwalają na bezpieczne przemieszczanie kosztów pomiędzy ograniczeniami. Trzy podstawowe operacje przeniesienia kosztów to:

Projekt: transfer kosztów z ograniczeń do ograniczeń jednoargumentowych
ProjectUnary : transfer kosztów z ograniczenia jednoargumentowego do ograniczenia zerowego
Rozszerz: przeniesienie kosztów z jednoargumentowego ograniczenia do ograniczenia

Basic Equivalence Preserving Transformations

Podstawowe przekształcenia zachowujące równoważność.

Celem transformacji zachowujących równoważność jest skoncentrowanie kosztów na ograniczeniu zerowym $displaystyle$ instancji i wartości z kosztem dodanym do , który do $c_ {\ pusty zestaw}}$ jest większy lub równy kosztowi zabronionemu lub kosztowi najlepszego dotychczas znalezionego rozwiązania. Metoda rozgałęzień i ograniczeń jest zwykle używana do rozwiązywania WCSP, z dolną granicą $displaystyle$ granicą $k}$ .

Podejście bez operacji przenoszenia kosztów

Alternatywą dla algorytmów transferu kosztów jest algorytm PFC-MRDAC , który jest klasycznym algorytmem rozgałęzienia i ograniczeń, który oblicza dolną granicę $węźle$ drzewa wyszukiwania, co odpowiada niedoszacowaniu kosztu dowolne rozwiązanie, które można uzyskać z tego węzła. Koszt najlepszego znalezionego rozwiązania wynosi ${\ displaystyle ub}$ . Kiedy ${\ displaystyle lb \ geq ub}$ , drzewo wyszukiwania z tego węzła jest przycinane.

Inne nowsze podejście opiera się na superreparametryzacji, która pozwala rozluźnić problem w celu obliczenia ściślejszych granic.

Rozwiązanie n-arnych WCSP

Wykazano, że algorytmy transferu kosztów są szczególnie skuteczne w rozwiązywaniu rzeczywistych problemów, gdy miękkie ograniczenia są binarne lub trójskładnikowe (maksymalna liczba ograniczeń w problemie jest równa 2 lub 3). W przypadku miękkich więzów o dużej arytmetyce transfer kosztów staje się poważnym problemem, ponieważ należy kontrolować ryzyko eksplozji kombinatorycznej .

Zaproponowano algorytm o nazwie Generalized Arc Consistency ( $GAC) w celu$ i ich koszty. Algorytm ten łączy w sobie dwie techniki, a mianowicie prostą redukcję tabelaryczną ( STR ) i przeniesienie kosztów. Wartości, które nie są już spójne w odniesieniu do GAC, są identyfikowane i obliczane są minimalne koszty wartości. Jest to szczególnie przydatne do wydajnego wykonywania operacji projekcji, które są wymagane do ustanowienia GAC.

Zbadano również funkcje kosztu globalnego z dedykowaną semantyką (np. SoftAllDifferent, SoftAmong) i policzasową złożonością.

Solvery

https://www.ics.uci.edu/~dechter/software.html
https://miat.inrae.fr/toulbar2 (na podstawie operacji przeniesienia kosztów)

Wzorce

Wiele rzeczywistych testów porównawczych WCSP jest dostępnych na http://genoweb.toulouse.inra.fr/~degivry/evalgm i https://forgemia.inra.fr/thomas.schiex/cost-function-library (starsza wersja na http ://costfunction.org/en/benchmark ). Więcej testów porównawczych MaxCSP jest dostępnych na http://www.cril.univ-artois.fr/~lecoutre/#/benchmarks (przestarzała witryna, zobacz też http://xcsp.org/series ).

Zobacz też