Wykrywanie kroków

Przykłady sygnałów, które mogą zawierać kroki uszkodzone przez szum. (a) stosunki liczby kopii DNA z danych z mikromacierzy , (b) natężenie promieniowania kosmicznego z monitora neutronowego , (c) prędkość obrotowa w funkcji czasu silnika wiciowego R. Sphaeroides oraz (d) intensywność czerwonego piksela z pojedynczej linii skanowania obraz cyfrowy.

W statystyce i przetwarzaniu sygnałów wykrywanie kroków (znane również jako wygładzanie kroków , filtrowanie kroków , wykrywanie przesunięć , wykrywanie skoków lub wykrywanie krawędzi ) to proces znajdowania nagłych zmian (kroków, skoków, przesunięć) średniego poziomu szeregu czasowego lub sygnał. Zwykle uważa się to za szczególny przypadek metody statystycznej znanej jako wykrywanie zmian lub zmienić wykrywanie punktu. Często krok jest mały, a szereg czasowy jest zniekształcony przez jakiś szum , co sprawia, że problem jest trudny, ponieważ krok może być ukryty przez szum. Dlatego często wymagane są algorytmy statystyczne i/lub przetwarzania sygnałów.

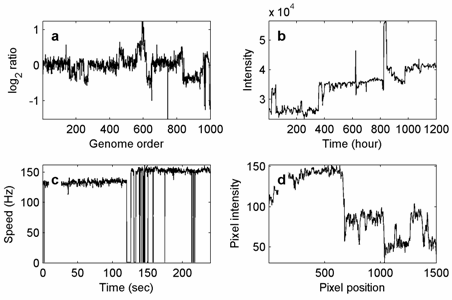
Problem wykrywania stopni występuje w wielu kontekstach naukowych i inżynierskich, na przykład w statystycznej kontroli procesu ( wykres kontrolny jest metodą najbardziej bezpośrednio powiązaną), w geofizyce eksploracyjnej (gdzie problemem jest podzielenie zapisu dziennika odwiertu na strefy stratygraficzne ), w genetyce (problem rozdzielania danych z mikromacierzy na podobne reżimy liczby kopii ) oraz w biofizyce (wykrywanie przejść stanów w maszynie molekularnej jak zapisano w śladach czasowo-pozycyjnych). W przypadku sygnałów 2D powiązany problem wykrywania krawędzi był intensywnie badany pod kątem przetwarzania obrazu .

Algorytmy

Kiedy wykrywanie kroków musi być wykonywane w momencie nadejścia danych, zwykle stosuje się algorytmy online i staje się to szczególnym przypadkiem analizy sekwencyjnej . Do takich algorytmów należy klasyczna CUSUM stosowana do zmian średniej.

Z kolei algorytmy offline są stosowane do danych potencjalnie długo po ich otrzymaniu. Większość algorytmów offline do wykrywania kroków w danych cyfrowych można podzielić na metody odgórne , oddolne , przesuwne lub globalne .

Z góry na dół

Algorytmy te zaczynają się od założenia, że nie ma kroków i wprowadzają możliwe kroki kandydujące pojedynczo, testując każdego kandydata, aby znaleźć ten, który minimalizuje niektóre kryteria (takie jak dopasowanie metodą najmniejszych kwadratów oszacowanego, bazowego sygnału o stałej częściowej). Przykładem jest rozmieszczania skoków krokowych , po raz pierwszy badany w problemach geofizycznych, który znalazł ostatnio zastosowanie we współczesnej biofizyce.

Od dołu do góry

Algorytmy oddolne przyjmują podejście „przeciwne” do metod odgórnych, najpierw zakładając, że między każdą próbką w sygnale cyfrowym występuje krok, a następnie sukcesywnie łącząc kroki w oparciu o pewne kryteria przetestowane dla każdego potencjalnego połączenia.

Okno przesuwne

Biorąc pod uwagę małe „okno” sygnału, algorytmy te szukają dowodów na krok występujący w tym oknie. Okno „przesuwa się” po szeregu czasowym, krok po kroku. Dowody na krok są testowane za pomocą procedur statystycznych, na przykład za pomocą testu t-Studenta dla dwóch prób . Alternatywnie do sygnału stosuje się filtr nieliniowy , taki jak filtr medianowy . Filtry takie jak te próbują usunąć szum, zachowując nagłe kroki.

Światowy

Algorytmy globalne biorą pod uwagę cały sygnał za jednym razem i próbują znaleźć kroki w sygnale za pomocą pewnego rodzaju procedury optymalizacji. Algorytmy obejmują falkowe i całkowite odszumianie zmienności , które wykorzystuje metody optymalizacji wypukłej . Tam, gdzie kroki można modelować jako łańcuch Markowa , często stosuje się również ukryte modele Markowa (podejście popularne w środowisku biofizyków). Gdy istnieje tylko kilka unikalnych wartości średniej, można również zastosować grupowanie k-średnich .

Liniowe i nieliniowe metody przetwarzania sygnałów do wykrywania kroków

Ponieważ kroki i (niezależny) szum mają teoretycznie nieskończoną szerokość pasma , a zatem nakładają się na podstawę Fouriera , podejścia przetwarzania sygnału do wykrywania kroków generalnie nie wykorzystują klasycznych technik wygładzania, takich jak filtr dolnoprzepustowy . Zamiast tego większość algorytmów jest wyraźnie nieliniowa lub zmienna w czasie.

Wykrywanie kroków i odcinkowo stałe sygnały

Ponieważ celem wykrywania kroków jest znalezienie serii chwilowych skoków średniej sygnału, pożądany, bazowy, średni sygnał jest fragmentarycznie stały . Z tego powodu wykrywanie kroków można z zyskiem postrzegać jako problem odzyskiwania fragmentarycznie stałego sygnału zniekształconego przez szum. Istnieją dwa uzupełniające się modele dla fragmentarycznie stałych sygnałów: jako splajny 0 stopni z kilkoma węzłami lub jako zestawy poziomów z kilkoma unikalnymi poziomami. Dlatego wiele algorytmów wykrywania kroków najlepiej rozumieć jako metody dopasowania splajnu 0 stopni lub odzyskiwania zestawu poziomów.

Wykrywanie kroków jako przywracanie ustawionego poziomu

Gdy istnieje tylko kilka unikalnych wartości średniej, odpowiednie są techniki grupowania, takie jak grupowanie k-średnich lub przesunięcie średniej . Techniki te są najlepiej rozumiane jako metody znajdowania opisu zestawu poziomów podstawowego, fragmentarycznie stałego sygnału.

Wykrywanie stopni jako dopasowanie splajnu 0 stopni

Wiele algorytmów wyraźnie dopasowuje splajny 0 stopni do zaszumionego sygnału w celu wykrycia kroków (w tym metody umieszczania skoków krokowych), ale istnieją inne popularne algorytmy, które można również postrzegać jako metody dopasowywania splajnów po pewnej transformacji, na przykład odszumianie całkowitej zmienności .

Uogólnione wykrywanie kroków przez fragmentaryczne stałe odszumianie

Wszystkie wymienione powyżej algorytmy mają pewne zalety i wady w określonych okolicznościach, jednak zaskakująco duża liczba tych algorytmów wykrywania kroków to szczególne przypadki bardziej ogólnego algorytmu. Algorytm ten polega na minimalizacji globalnego funkcjonału:

{\ Displaystyle H [m] = \ suma _ {i=1}^{N}\suma _{j=1}^{N}\Lambda (x_{i}-m_{j},m_{i}-m_{j},x_{i}-x_ {j},ij)}

()

Tutaj x _i dla i = 1, ...., N jest sygnałem wejściowym w czasie dyskretnym o długości N , a m _i jest sygnałem wyjściowym algorytmu. Celem jest zminimalizowanie H [ m ] w odniesieniu do sygnału wyjściowego m . Postać funkcji $.$ konkretny algorytm Na przykład wybierając:

{\ Displaystyle \ Lambda = {\ Frac {1} {2}} \ lewo | x_ {i} -m_ {j} \ prawo | ^ {2} ja (ij = 0) + \gamma \left|m_{i}-m_{j}\right|I(ij=1)}

gdzie ja ( S ) = 0, jeśli warunek S jest fałszywy, a jeden w przeciwnym razie, uzyskuje algorytm odszumiania całkowitej zmienności z $regularyzacji$ . Podobnie:

{\ Displaystyle \ Lambda = \ min \ lewo \ {{\ Frac {1} {2}} \ lewo | m_ {i} -m_ {j} \ prawo | ^ {2}, W \ prawo \ }}

prowadzi do algorytmu przesunięcia średniego , gdy używany jest integrator Eulera o adaptacyjnym rozmiarze kroku, inicjalizowany sygnałem wejściowym x . Tutaj W > 0 jest parametrem, który określa wsparcie jądra przesunięcia średniego. Innym przykładem jest:

{\ Displaystyle \ Lambda = {\ Frac {1- \ exp (- \ beta |m_{i}-m_{j}|^{2}/2)}{\beta }}\cdot I(|ij|\leq W)}

$prowadząc$ do filtra dwustronnego , gdzie tonalnym parametrem jądra, a jest przestrzennym wsparciem jądra. Jeszcze innym szczególnym przypadkiem jest:

{\ Displaystyle \ Lambda = {\ Frac {1} {2}} \ lewo | x_ {i} -m_ {j} \ prawo | ^ {2} ja (ij = 0) + \gamma \left|m_{i}-m_{j}\right|^{0}I(ij=1)}

określenie grupy algorytmów, które próbują zachłannie dopasować splajny 0 stopni do sygnału. Tutaj, ${\ displaystyle \ scriptstyle \ lewo | x \ prawo | ^ {0}}$ jest zdefiniowane jako zero, jeśli x = 0, a jeden w przeciwnym razie.

Wiele funkcjonałów w równaniu ( 1 ) zdefiniowanych przez konkretny wybór jest wypukłych : można $za$ zminimalizować pomocą metod optymalizacji wypukłej . Jeszcze inne nie są wypukłe, ale opracowano szereg algorytmów minimalizujących te funkcjonały.

Wykrywanie kroków za pomocą modelu Pottsa

Klasyczną metodą wariacyjną wykrywania kroków jest model Pottsa. Daje to problem optymalizacji niewypukłej

{\ Displaystyle u ^ {*} = \ arg \ min _ {u \ w \ mathbb {R} ^ {N} }\gamma \|\nabla u\|_{0}+\|ux\|_{p}^{p}}

Termin ${\ Displaystyle \|\ nabla u \|_ {0} = \ # \ {i: u_ {i} \ neq u_ {i + 1}\}}$ penalizuje liczbę skoków i wyraz ${\ Displaystyle \|ux \|_ {p} ^ {p} = \ suma _ {i = 1} ^ {N} | u_ {i} -x_ {i} | ^ {p}} mierzy wierność$ danych x . Parametr γ > 0 kontroluje kompromis między regularnością a wiernością danych . Ponieważ minimalizator $,$ kroki są określone przez niezerowe lokalizacje gradientu $}}$ . p ${\ displaystyle p = 2}$ i $p = 1}$ istnieją szybkie algorytmy, które dają dokładne rozwiązanie problemu Pottsa w ${\ Displaystyle O (N ^ {2})}$ .

Zobacz też

Segmentacja szeregów czasowych

Linki zewnętrzne