Zasada dodawania

A collection of five dots and one of zero dots merge into one of five dots.

5+0=5 ilustrowane zbiorami kropek.

W kombinatoryce zasada dodawania lub reguła sumy jest podstawową zasadą liczenia . Mówiąc prościej, jest to intuicyjny pomysł, że jeśli mamy kilka sposobów zrobienia czegoś i B liczbę sposobów zrobienia innej rzeczy i nie możemy zrobić obu jednocześnie, to są ${\ displaystyle A + B}$ sposoby wyboru jednej z akcji. Z matematycznego punktu widzenia zasada dodawania mówi, że dla zbiorów rozłącznych A i B mamy ${\ Displaystyle | A \ kubek B | = | A | + | B |}$ .

Reguła sumy jest faktem dotyczącym teorii mnogości . ^{[ potrzebne źródło ]}

Zasadę dodawania można rozszerzyć na kilka zestawów. Jeśli ${\ Displaystyle S_ {1}, S_ {2}, \ ldots, S_ {n}}$ są parami rozłącznymi zbiorami, to mamy:

{\ Displaystyle | S_ {1} | + | S_ {2} | + \ cdots + | S_ {n} | = | S_ {1} \ kubek S_ {2} \ kubek \ cdots \ kubek S_ {n} |. }

Twierdzenie to można udowodnić z zasady dodawania przez indukcję względem n .

Prosty przykład

Five shapes split into a group of three shapes and one of two shapes.

3+2=5 ilustrowane kształtami.

Pewna osoba zdecydowała się dziś na zakupy w jednym sklepie w północnej lub południowej części miasta. Jeśli odwiedzą północną część miasta, zrobią zakupy w centrum handlowym, sklepie meblowym lub sklepie jubilerskim (3 sposoby). Jeśli odwiedzą południową część miasta, zrobią zakupy w sklepie odzieżowym lub obuwniczym (2 sposoby).

Tak więc istnieje $, w których$ dana osoba mogłaby dziś zrobić zakupy.

Zasada włączenia-wyłączenia

A series of Venn diagrams illustrating the principle of inclusion-exclusion.

Seria diagramów Venna ilustrujących zasadę włączenia-wyłączenia.

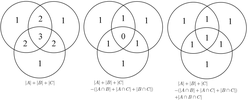
Zasada włączenia-wykluczenia (znana również jako zasada sita ) może być traktowana jako uogólnienie reguły sumy, ponieważ również wylicza liczbę elementów w zjednoczeniu niektórych zbiorów (ale nie wymaga, aby zbiory były rozłączne ). Stwierdza, że jeśli An _A 1 _, ..., są zbiorami skończonymi, to

{\ Displaystyle \ lewo | \ bigcup _ {i = 1} ^ {n} A_ {i} \ prawo | = \ suma _ {i = 1} ^ {n} \ lewo | A_ {i} \ prawo | - \ suma _{i,j\,:\,1\równoważnik i<j\równoważnik n}\left|A_{i}\cap A_{j}\right|+\sum _{i,j,k\,: \,1\leq i<j<k\leq n}\left|A_{i}\cap A_{j}\cap A_{k}\right|-\ \cdots \ +(-1)^{n- 1}\left|A_{1}\cap \cdots \cap A_{n}\right|.}

Zasada odejmowania

Podobnie, dla danego zbioru skończonego S i innego zbioru $jeśli$ to ${\ Displaystyle | A ^ {c} | = | S | - | A |}$ . Aby to udowodnić, zauważ, że ${\ Displaystyle | A ^ {c}|+|A|=|S|}$ na zasadzie dodawania.

Aplikacje

Zasada dodawania może być wykorzystana do udowodnienia reguły Pascala w sposób kombinatoryczny. Aby obliczyć $.$ to potraktować jako liczbę sposobów wybrania k pokoju zawierającego n dzieci 1 $Następnie$ istnieją wybierania ludzi bez ${\ displaystyle {\ binom {n} {k-1}}}$ sposoby wybierania osób, w tym nauczyciela. Zatem ${\ Displaystyle {\ binom {n + 1} {k}} = {\ binom {n} {k}} + {\ binom { n}{k-1}}}$ .

Zasadę dodawania można również wykorzystać do udowodnienia zasady mnożenia .

Bibliografia

Biggs, Norman L. (2002). Matematyka dyskretna . Indie: Oxford University Press . ISBN 978-0-19-871369-2 .

Zobacz też