Dominujący zestaw

Trzy dominujące zestawy tego samego wykresu (na czerwono). Liczba dominacji tego wykresu to 2: (b) i (c) pokazują, że istnieje zbiór dominujący z 2 wierzchołkami i nie ma zbioru dominującego z tylko 1 wierzchołkiem.

W teorii grafów dominującym zbiorem grafu G $jest$ podzbiór $D$ jego wierzchołków, taki że dowolny wierzchołek G $jest$ albo w $D$ , albo ma sąsiada w $D$ . Liczba dominacji $γ(G)$ to liczba wierzchołków w najmniejszym zbiorze dominującym dla $G$ .

Problem zbioru dominującego dotyczy sprawdzenia, czy $γ(G) \leq K$ dla danego grafu $G$ i wejścia $K$ ; jest to klasyczny NP-zupełny problem decyzyjny w teorii złożoności obliczeniowej . Dlatego uważa się, że może nie być wydajnego algorytmu , który mógłby obliczyć $γ(G)$ dla wszystkich grafów $G$ . Istnieją jednak wydajne algorytmy aproksymacyjne , jak również wydajne algorytmy dokładne dla niektórych klas grafów.

Zestawy dominujące mają praktyczne znaczenie w kilku obszarach. W sieciach bezprzewodowych zestawy dominujące służą do znajdowania wydajnych tras w sieciach komórkowych ad-hoc. Wykorzystywano je również w podsumowaniu dokumentów oraz w projektowaniu bezpiecznych systemów dla sieci elektroenergetycznych .

Definicja formalna

Biorąc pod uwagę wykres nieskierowany $, setminus u \in V u$ podzbiór wierzchołków nazywany jest $re}$ dominującym $,$ jeśli dla każdego wierzchołka $w V$ ${\ displaystyle (u, v) \ in$ istnieje wierzchołek $E$ , że .

Każdy wykres ma co najmniej jeden zestaw dominujący: jeśli zbiór wszystkich wierzchołków, to z definicji D $,$ dominującym ponieważ nie ma wierzchołka $displaystyle u\in V\setminus D}$ . Bardziej interesującym wyzwaniem jest znalezienie małych dominujących zestawów. Liczba dominacji G jest zdefiniowana jako: ${\ Displaystyle \ gamma (G): = \ min \ {| D |: D {\ tekst { jest dominującym zbiorem }} G \}}$ $=$ .

Warianty

Spójny zestaw dominujący to zbiór dominujący, który jest również spójny . Jeśli S jest połączonym zbiorem dominującym, można utworzyć drzewo rozpinające G , w którym S tworzy zbiór nieliściastych wierzchołków drzewa; odwrotnie, jeśli T jest dowolnym drzewem rozpinającym na grafie z więcej niż dwoma wierzchołkami, wierzchołki T nie będące liśćmi tworzą połączony zbiór dominujący. Dlatego znalezienie minimalnych spójnych zbiorów dominujących jest równoznaczne ze znalezieniem drzew rozpinających o maksymalnej możliwej liczbie liści.

Całkowity zbiór dominujący (lub zbiór silnie dominujący ) to zbiór wierzchołków, w którym wszystkie wierzchołki w grafie, w tym same wierzchołki w zbiorze dominującym, mają sąsiada w zbiorze dominującym. To znaczy: dla każdego wierzchołka $, v) \w E}$ $wierzchołek$ taki $u$ u . Rysunek (c) powyżej przedstawia zestaw dominujący, który jest połączonym zestawem dominującym i całkowitym zestawem dominującym; przykłady na rysunkach (a) i (b) nie są żadne. W przeciwieństwie do prostego zestawu dominującego, całkowity zestaw dominujący może nie istnieć. Na przykład graf z jednym lub więcej wierzchołkami i bez krawędzi nie ma całkowitego zbioru dominującego. Silna liczba dominacji G $jest$ zdefiniowana jako: ${\ Displaystyle \ gamma ^ {strong} (G): = \ min \ {| D |: D {\ tekst { jest silnie dominującym zbiorem}} G \} }$ ; oczywiście ${\ Displaystyle \ gamma ^ {silny} (G) \ geq \ gamma (G)}$ .

Dominujący zestaw krawędzi to zbiór krawędzi (par wierzchołków), których suma jest zbiorem dominującym; taki zestaw może nie istnieć (na przykład graf z jednym lub więcej wierzchołkami i bez krawędzi go nie ma). Jeśli istnieje, to połączenie wszystkich jego krawędzi jest zbiorem silnie dominującym. $_$ najmniejszy _

W przeciwieństwie do tego, zbiór dominujący na krawędziach to zbiór D krawędzi, taki że każda krawędź spoza D sąsiaduje z co najmniej jedną krawędzią z D ; taki zestaw zawsze istnieje (na przykład zbiór wszystkich krawędzi jest zbiorem dominującym na krawędzi).

Zbiór k -dominujący to zbiór wierzchołków taki, że każdy wierzchołek nienależący do zbioru ma co najmniej k sąsiadów w zbiorze (standardowy zbiór dominujący to zbiór dominujący 1). Podobnie, dominujący zbiór k -krotek to zbiór wierzchołków taki, że każdy wierzchołek grafu ma co najmniej k sąsiadów w zbiorze (całkowity zbiór dominujący to zbiór dominujący o 1 krotce). $(1 + log n)$ -przybliżenie minimalnego zbioru dominującego k -krotki można znaleźć w czasie wielomianowym. Każdy graf dopuszcza k -dominujący (na przykład zbiór wszystkich wierzchołków); ale tylko grafy o minimalnym stopniu $k - 1$ dopuszczają zbiór dominujący k - krotki. Jednak nawet jeśli graf dopuszcza k - krotki, minimalny zbiór dominujący k - krotki może być prawie k razy większy niż minimalny zbiór dominujący k dla tego samego grafu; $(1,7 + log Δ)$ -przybliżenie minimalnego zbioru k -dominującego można również znaleźć w czasie wielomianowym.

Zbiór dominujący w gwiazdach to podzbiór D z V taki, że dla każdego wierzchołka v w V , gwiazda v ( zbiór krawędzi sąsiadujących z v ) przecina gwiazdę jakiegoś wierzchołka w D . Oczywiście, jeśli G ma izolowane wierzchołki , to nie ma zbiorów dominujących w gwiazdach (ponieważ gwiazda izolowanych wierzchołków jest pusta). Jeśli G nie ma izolowanych wierzchołków, to każdy zbiór dominujący jest zbiorem dominującym w gwiazdę i odwrotnie. Rozróżnienie między dominacją gwiazd i zwykłą dominacją jest bardziej znaczące, gdy weźmie się pod uwagę ich ułamkowe warianty.

Domatyczny podział to podział wierzchołków na rozłączne zbiory dominujące. Numer domatic to maksymalny rozmiar partycji domatic.

Wieczny zbiór dominujący to dynamiczna wersja dominacji, w której wierzchołek v w zbiorze dominującym D jest wybierany i zastępowany sąsiadem u ( u nie jest w D ) tak, że zmodyfikowany D jest również zbiorem dominującym i proces ten można powtórzyć nad dowolnym nieskończonym ciągiem wyborów wierzchołków v .

Zestawy dominujące i niezależne

Zbiory dominujące są blisko spokrewnione ze zbiorami niezależnymi : zbiór niezależny jest także zbiorem dominującym wtedy i tylko wtedy, gdy jest zbiorem niezależnym maksymalnym , więc każdy maksymalny zbiór niezależny na grafie jest z konieczności także minimalnym zbiorem dominującym.

Dominacja niezależnych zestawów

Zestaw dominujący może, ale nie musi, być zestawem niezależnym. Na przykład, rysunki (a) i (b) powyżej przedstawiają niezależne zestawy dominujące, podczas gdy rysunek (c) ilustruje zestaw dominujący, który nie jest zestawem niezależnym.

Niezależna liczba dominacji $i (G)$ grafu $G$ jest wielkością najmniejszego zbioru dominującego, który jest zbiorem niezależnym. Równoważnie, jest to rozmiar najmniejszego maksymalnego niezależnego zestawu. Minimum w $i (G)$ jest przejmowane przez mniej elementów (rozważane są tylko zbiory niezależne), więc $γ (G) \leq i (G)$ dla wszystkich grafów $G$ .

Nierówność może być ścisła - istnieją wykresy $G$ , dla których $γ (G)< i (G)$ . Na przykład, niech $G$ będzie wykresem podwójnej gwiazdy składającym się z wierzchołków ${\ Displaystyle x_ {1}, \ ldots, x_ {p}, a, b,y_{1},\ldots,y_{q}}$ , gdzie $p, q > 1$ . Krawędzie $G$ są zdefiniowane w następujący sposób: każdy $x i$ sąsiaduje z $a$ , $a$ sąsiaduje z $b$ , a $b$ sąsiaduje z każdym $y j$ . Wtedy $γ(G) = 2,$ ponieważ ${a, b}$ jest najmniejszym zbiorem dominującym. Jeśli $p \leq q$ , to $ja (sol) = p + 1$ ponieważ ${\ Displaystyle \ {x_ {1}, \ ldots, x_ {p}, b \}}$ jest najmniejszy zbiór dominujący, który jest jednocześnie niezależny (jest to najmniejszy zbiór maksymalny niezależny).

Istnieją rodziny grafów, w których $γ(G) = i (G)$ , to znaczy każdy minimalny maksymalny niezależny zbiór jest minimalnym zbiorem dominującym. Na przykład $γ(G) = i (G)$ , jeśli $G$ jest grafem bez pazurów .

Graf $G$ nazywany jest grafem z dominacją idealną, jeśli $γ (H) = i (H)$ w każdym indukowanym podgrafie $H$ z $G$ . Ponieważ indukowany podgraf grafu bez pazurów jest pozbawiony pazurów, wynika z tego, że każdy graf bez pazurów jest również doskonały pod względem dominacji.

Dla dowolnego grafu $G$ jego wykres liniowy $L (G)$ jest wolny od pazurów, a zatem minimalny maksymalny niezależny zbiór w $L (G)$ jest również minimalnym zbiorem dominującym w $L (G)$ . Niezależny zestaw w $L (G)$ odpowiada dopasowaniu w G $,$ a zestaw dominujący w $L (G)$ odpowiada zestawowi dominującemu krawędzi w $G.$ Dlatego minimalne dopasowanie maksymalne ma taki sam rozmiar jak minimalny zestaw dominujący na krawędzi.

Dominacja niezależnych zestawów

Liczba dominacji niezależności $iγ (G)$ grafu $G$ jest maksimum, nad wszystkimi niezależnymi zbiorami $A$ z $G$ , najmniejszego zbioru dominującego $A$ . Dominowanie podzbiorów wierzchołków wymaga potencjalnie mniejszej liczby wierzchołków niż dominowanie wszystkich wierzchołków, więc $iγ (G) \leq γ (G)$ dla wszystkich grafów $G$ .

Nierówność może być ścisła – istnieją grafy $G$ , dla których $iγ (G)< γ (G)$ . Na przykład dla pewnej liczby całkowitej $n$ niech $G$ będzie grafem, w którym wierzchołki są wierszami i kolumnami tablicy $n$ -na- $n$ , a dwa takie wierzchołki są połączone wtedy i tylko wtedy, gdy się przecinają. Jedynymi niezależnymi zbiorami są zbiory tylko wierszy lub zbiory tylko kolumn, a każdy z nich może być zdominowany przez pojedynczy wierzchołek (kolumnę lub wiersz), więc $iγ (G) = 1$ . Aby jednak zdominować wszystkie wierzchołki, potrzebujemy co najmniej jednego wiersza i jednej kolumny, więc $γ (G) = 2$ . Ponadto stosunek między $γ (G) / iγ (G)$ może być dowolnie duży. Na przykład, jeśli wierzchołki $G$ są wszystkimi podzbiorami kwadratów planszy $n$ na $n$ , to nadal $iγ (G) = 1$ , ale $γ (G) = n$ .

Bi -niezależna liczba dominacji $iγi (G)$ grafu $G$ jest maksimum, spośród wszystkich niezależnych zbiorów $A$ z $G$ , najmniejszego niezależnego zbioru dominującego $A$ . Dla dowolnego grafu $G$ zachodzą następujące zależności :

{\ Displaystyle {\ rozpocząć {wyrównane} i (G) i \ geq \ gamma (G)\geq i\gamma (G)\\i(G)&\geq i\gamma i(G)\geq i\gamma (G)\end{wyrównane}}}

Historia

Problem dominacji był badany od lat pięćdziesiątych XX wieku, ale tempo badań nad dominacją znacznie wzrosło w połowie lat siedemdziesiątych. W 1972 roku Richard Karp udowodnił , że problem z okładką zestawu jest NP-zupełny . Miało to natychmiastowe implikacje dla problemu zbioru dominującego, ponieważ między tymi dwoma problemami istnieją proste wierzchołki do ustawienia i krawędź do nierozłącznego przecięcia. To dowiodło, że dominujący problem zbioru jest również NP-zupełny .

Algorytmy i złożoność obliczeniowa

Problem pokrycia zestawu jest dobrze znanym problemem NP-trudnym – decyzyjna wersja pokrycia zestawu była jednym z 21 problemów NP-zupełnych Karpa . Istnieje para redukcji L w czasie wielomianowym między problemem minimalnego zbioru dominującego a problemem pokrycia zbioru . Te redukcje ( patrz poniżej ) pokazują, że wydajny algorytm dla problemu minimalnego zbioru dominującego zapewniłby wydajny algorytm dla problemu zestawu pokrycia i odwrotnie. Co więcej, redukcje zachowują współczynnik aproksymacji : dla dowolnego α algorytm aproksymacji α w czasie wielomianowym dla minimalnych zbiorów dominujących zapewniłby algorytm aproksymacji α w czasie wielomianowym dla problemu pokrycia zestawu i odwrotnie. Oba problemy są w rzeczywistości Log-APX-complete .

Aproksymacja pokrycia zestawu jest również dobrze rozumiana: logarytmiczny współczynnik przybliżenia można znaleźć za pomocą prostego algorytmu zachłannego , a znalezienie sublogarytmicznego współczynnika przybliżenia jest NP-trudne. Mówiąc dokładniej, algorytm zachłanny zapewnia czynnik $1 + log| V |$ aproksymacja minimalnego zbioru dominującego, a żaden algorytm czasu wielomianowego nie może osiągnąć współczynnika aproksymacji lepszego niż $c log| V |$ dla pewnego $c > 0$ chyba że P = NP .

redukcje L

Następujące dwie redukcje pokazują, że problem minimalnego zbioru dominującego i problem pokrycia zbioru są równoważne przy L-redukcjach : biorąc pod uwagę przypadek jednego problemu, możemy skonstruować równoważny przypadek drugiego problemu.

Od zestawu dominującego do zestawu obejmującego

Biorąc pod uwagę graf $G = (V, E)$ z $V = {1, 2, ..., n},$ skonstruuj instancję okładki zestawu $(U, S)$ w następujący sposób: wszechświat $U$ to $V$ , a rodzina podzbiorów to $S = {S 1, S 2, ..., S n}$ takie, że $S v$ składa się z wierzchołka $v$ i wszystkich wierzchołków przylegających do $v$ w $G$ .

Teraz, jeśli $D$ jest zbiorem dominującym dla $G$ , to $C = {S v : v \in D}$ jest wykonalnym rozwiązaniem problemu zestawu pokrycia, gdzie $| C | = | D |$ . I odwrotnie, jeśli $C = {S v : v \in D}$ jest możliwym rozwiązaniem problemu zestawu pokrycia, to $D$ jest zbiorem dominującym dla $G$ , gdzie $| D | = | C |$ .

Stąd rozmiar minimalnego zestawu dominującego dla $G$ jest równy rozmiarowi minimalnego zestawu pokrycia dla $(U, S)$ . Ponadto istnieje prosty algorytm, który odwzorowuje zestaw dominujący na okładkę zestawu o tej samej wielkości i odwrotnie. W szczególności wydajny aproksymacji α dla pokrycia zestawu zapewnia wydajny algorytm aproksymacji α dla minimalnych zbiorów dominujących.

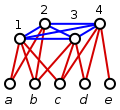
Na przykład, biorąc pod uwagę wykres

G

pokazany po prawej stronie, konstruujemy instancję zestawu okładek ze wszechświatem

U = {1, 2, ..., 6}

i podzbiorami

S 1 = {1, 2, 5},

S 2 = {1, 2, 3, 5},

S 3 = {2, 3, 4, 6},

S 4 = {3, 4},

S 5 = {1, 2, 5, 6}

i

S 6 = {3, 5, 6}.

W tym przykładzie

D = {3, 5}

jest zbiorem dominującym dla

G

– odpowiada to zbiorowi pokrycia

C = {S 3, S 5}.

Na przykład wierzchołek

4 \in V

jest zdominowany przez wierzchołek

3 \in D

, a element

4 \in U

jest zawarty w zbiorze

S 3 \in C

.

Od zestawu zakrywającego do zestawu dominującego

Niech $(S, U)$ będzie przykładem problemu zestawu okładek ze wszechświatem $U$ i rodziną podzbiorów $S = {S i : i \in I};$ zakładamy, że $U$ i zbiór indeksów $I$ są rozłączne. Skonstruuj graf $G = (V, E)$ w następujący sposób: zbiór wierzchołków to $V = I \cup U$ , istnieje krawędź ${i, j} \in E$ między każdą parą $i, j \in I$ , istnieje też krawędź ${ja, u}$ dla każdego $ja \in ja$ i $u \in S ja$ . Oznacza to, że $G$ jest grafem podzielonym : $I$ jest kliką , a $U$ jest niezależnym zbiorem .

Teraz, jeśli $C = {S i : i \in D}$ jest wykonalnym rozwiązaniem problemu zbioru pokrycia dla pewnego podzbioru $D \subseteq I$ , to $D$ jest zbiorem dominującym dla $G$ , gdzie $| D | = | C |$ : Po pierwsze, dla każdego $u \in U$ istnieje $i \in D$ takie, że $u \in S i$ , a konstrukcyjnie $u$ oraz $i$ sąsiadują w $G$ ; stąd $u$ jest zdominowane przez $i$ . Po drugie, ponieważ $D$ musi być niepuste, każdy $i \in I$ sąsiaduje z wierzchołkiem w $D$ .

I odwrotnie, niech $D$ będzie zbiorem dominującym dla $G$ . Wtedy możliwe jest skonstruowanie innego zbioru dominującego $X$ takiego, że $| X | \leq | D |$ i $X \subseteq I$ : po prostu zamień każde $u \in D \cap U$ na sąsiada $i \in I$ z $u$ . Wtedy $C = {S i : i \in X}$ jest wykonalnym rozwiązaniem problemu zestawu pokrycia, gdzie $| C | = | X | \leq | D |$ .

Ilustracja po prawej pokazuje konstrukcję dla

U = {a, b, c, d, e}, I = {1, 2, 3, 4},

S 1 = {a, b, c},

S 2 = {za, b},

S 3 = {b, do, re}

i

S 4 = {do, re, mi}.

W tym przykładzie

C = {S 1, S 4}

to zestaw okładek; odpowiada to dominującemu zestawowi

D = {1, 4}.

D = {a, 3, 4}

to kolejny dominujący zbiór dla grafu

G

. Biorąc pod uwagę

D

, możemy skonstruować dominujący zbiór

X = {1, 3, 4}

, który nie jest większy niż

D

i który jest podzbiorem

I

. Zbiór dominujący

X

odpowiada okładce zestawu

C = {S 1, S 3, S 4}.

Przypadki specjalne

Jeśli wykres ma maksymalny stopień Δ, to algorytm zachłannej aproksymacji znajduje $O (log Δ)$ -aproksymację minimalnego zbioru dominującego. Niech również $d g$ będzie licznością zbioru dominującego otrzymanego za pomocą zachłannego przybliżenia, a następnie zachodzi następująca relacja, ${\ Displaystyle d_ {g} \ równoważnik N + 1- {\ sqrt {2M + 1}}}$ , gdzie $N$ to liczba węzłów, a $M$ to liczba krawędzi danego grafu nieskierowanego. Dla ustalonego Δ kwalifikuje się to jako dominujący zestaw dla członkostwa APX ; w rzeczywistości jest APX-kompletny.

Problem dopuszcza schemat aproksymacji w czasie wielomianowym (PTAS) dla szczególnych przypadków, takich jak grafy dysków jednostkowych i grafy planarne . Minimalny zestaw dominujący można znaleźć w czasie liniowym na grafach szeregowo-równoległych .

Dokładne algorytmy

Minimalny zbiór dominujący grafu $n$ -wierzchołków można znaleźć w czasie $O (2 n n)$ , sprawdzając wszystkie podzbiory wierzchołków. Fomin, Grandoni i Kratsch (2009) pokazują, jak znaleźć minimalny zbiór dominujący w czasie $O (1,5137 n)$ i przestrzeni wykładniczej oraz w czasie $O (1,5264 n)$ i przestrzeni wielomianowej. Szybszy algorytm wykorzystujący $O (1,5048 n)$ został znaleziony przez van Rooij, Nederlof i van Dijk (2009) , którzy również wykazali, że w tym czasie można obliczyć liczbę minimalnych zestawów dominujących. Liczba minimalnych zbiorów dominujących wynosi co najwyżej $1,7159 n$ i wszystkie takie zbiory można wymienić w czasie $O (1,7159 n)$ .

Złożoność parametryczna

Znalezienie dominującego zbioru o rozmiarze $k$ odgrywa kluczową rolę w teorii złożoności parametrycznej. Jest to najbardziej znany problem kompletny dla klasy W[2] i używany w wielu redukcjach, aby pokazać trudność innych problemów. W szczególności problem nie jest rozwiązywany przy użyciu stałych parametrów w tym sensie, że nie istnieje żaden algorytm z czasem działania $f (k) n O(1)$ dla dowolnej funkcji $f$ , chyba że hierarchia W zwinie się do FPT=W[2].

Z drugiej strony, jeśli graf wejściowy jest planarny, problem pozostaje NP-trudny, ale znany jest algorytm o stałych parametrach. W rzeczywistości problem ma jądro o rozmiarze liniowym w $k$ , a czasy wykonywania, które są wykładnicze w √ k i sześcienne w $n$ , można uzyskać, stosując programowanie dynamiczne do rozkładu gałęzi jądra. Mówiąc bardziej ogólnie, problem zbioru dominującego i wiele wariantów tego problemu można rozwiązać ze stałymi parametrami, gdy jest sparametryzowany zarówno przez rozmiar zbioru dominującego, jak i rozmiar najmniejszego zabronionego kompletnego podgrafu dwudzielnego ; to znaczy, problemem jest FPT na grafach bez biclique , bardzo ogólnej klasie rzadkich grafów, która obejmuje grafy planarne.

Zestaw komplementarny do zestawu dominującego, nonblocker , można znaleźć za pomocą algorytmu o stałych parametrach na dowolnym wykresie.

Zobacz też

Hipoteza Vizinga - wiąże liczbę dominacji iloczynu kartezjańskiego grafów z liczbą dominacji jego czynników.
Ustaw problem z okładką
Numer niewoli
Nonblocker - uzupełnienie zestawu dominującego.

Notatki

Alber, Jochen; Stypendyści, Michael R .; Niedermeier, Rolf (2004), „Redukcja danych w czasie wielomianowym dla zbioru dominującego”, Journal of the ACM , 51 (3): 363–384, arXiv : cs/0207066 , doi : 10.1145/990308.990309 , S2CID 488501 .
Allan, Robert B.; Laskar, Renu (1978), „O dominacji i niezależnych liczbach dominacji wykresu”, Discrete Mathematics , 23 (2): 73–76, doi : 10.1016 / 0012-365X (78) 90105-X .
Crescenzi, Pierluigi; Kann, Viggo; Halldórsson, Magnus; Karpiński, Marek ; Woeginger, Gerhard (2000), „Minimalny zestaw dominujący”, Kompendium problemów optymalizacji NP .
Dehne, Frank; Stypendyści, Michael; Fernau, Henning; Prieto, Elena; Rosamond , Frances ( 2006 ) , Notatki z wykładów z informatyki, tom. 3831, Springer, s. 237–245, doi : 10.1007/11611257_21 .
Escoffier, Bruno; Paschos, Vangelis Th. (2006), „Kompletność w klasach aproksymacji poza APX”, Teoretyczna informatyka , 359 (1–3): 369–377, doi : 10.1016/j.tcs.2006.05.023
Faudree, Ralph ; Flandrin, Evelyne; Ryjáček, Zdeněk (1997), „Wykresy bez pazurów - ankieta”, Matematyka dyskretna , 164 (1–3): 87–147, doi : 10.1016/S0012-365X (96) 00045-3 , MR 1432221 .
Fomin, Fedor V.; Grandoni, Fabrizio; Kratsch, Dieter (2009), „Podejście miary i podboju do analizy dokładnych algorytmów”, Journal of the ACM , 56 (5): 25: 1–32, doi : 10.1145/1552285.1552286 , S2CID 1186651 .
Fomin, Fedor V.; Grandoni, Fabrizio; Piatkin, Artem; Stepanov, Alexey (2008), „Granice kombinatoryczne poprzez pomiar i podbijanie: ograniczanie minimalnych dominujących zestawów i aplikacji”, ACM Transactions on Algorithms , 5 (1): 9: 1–17, doi : 10.1145/1435375.1435384 , S2CID 2489447 .
Fomin, Fedor V.; Thilikos, Dimitrios M. (2006), „Zbiory dominujące w grafach planarnych: szerokość gałęzi i przyspieszenie wykładnicze”, SIAM Journal on Computing , 36 (2): 281, doi : 10.1137/S0097539702419649 , S2CID 5232238 .
Förster, Klaus-Tycho. (2013), „Przybliżona dominacja odporna na błędy w ogólnych wykresach”, Proc. z Dziesiątych Warsztatów Algorytmiki Analitycznej i Kombinatoryki ANALCO , SIAM, s. 25–32, doi : 10.1137 / 1.9781611973037.4 , ISBN 978-1-61197-254-2 .
Garey, Michael R .; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness , WH Freeman , ISBN 0-7167-1045-5 , s. 190, problem GT2.
Hedetniemi, ST; Laskar, RC (1990), „Bibliografia dotycząca dominacji na wykresach i niektóre podstawowe definicje parametrów dominacji”, Discrete Mathematics , 86 (1–3): 257–277, doi : 10.1016 / 0012-365X (90) 90365-O .
Kann, Viggo (1992), O zbliżeniu problemów optymalizacji NP-zupełnej (PDF) . Praca doktorska, Department of Numerical Analysis and Computing Science, Royal Institute of Technology , Sztokholm {{ cytowanie }} : CS1 maint: postscriptum ( link ) .
Klasing, Ralf; Laforest, Christian (2004), „Wyniki twardości i algorytmy aproksymacji dominacji k-krotek na wykresach”, Information Processing Letters , 89 (2): 75–83, doi : 10.1016/j.ipl.2003.10.004 .
Papadimitriou, Christos H.; Yannakakis, Mihailis (1991), „Optymalizacja, przybliżenie i klasy złożoności”, Journal of Computer and System Sciences , 43 (3): 425–440, doi : 10.1016 / 0022-0000 (91) 90023-X
Parekh, Abhay K. (1991), „Analiza zachłannej heurystyki do znajdowania małych dominujących zestawów na grafach”, Information Processing Letters , 39 (5): 237–240, doi : 10.1016/0020-0190 (91) 90021-9
Raz, R .; Safra, S. (1997), „Test niskiego stopnia prawdopodobieństwa błędu sub-stałego i charakterystyka PCP prawdopodobieństwa błędu sub-stałego NP”, Proc. 29. doroczne sympozjum ACM na temat teorii informatyki , ACM, s. 475–484, doi : 10.1145/258533.258641 , ISBN 0-89791-888-6 , S2CID 15457604 .
Takamizawa, K.; Nishizeki, T .; Saito, N. (1982), „Obliczalność w czasie liniowym problemów kombinatorycznych na grafach szeregowo-równoległych”, Journal of the ACM , 29 (3): 623–641, doi : 10.1145 / 322326.322328 , S2CID 16082154 .
Telle, Jan Arne; Villanger, Yngve (2012), „Algorytmy FPT do dominacji w grafach bez biclique”, w: Epstein, Leah; Ferragina, Paolo (red.), Algorytmy - ESA 2012: 20. doroczne sympozjum europejskie, Lublana, Słowenia, 10–12 września 2012 r., Proceedings , Lecture Notes in Computer Science , tom. 7501, Springer, s. 802–812, doi : 10.1007/978-3-642-33090-2_69 .
van Rooij, JMM; Nederlof, J.; van Dijk, TC (2009), „Włączenie / wykluczenie spotyka się z pomiarem i zwyciężaniem: dokładne algorytmy liczenia dominujących zestawów”, Proc. 17. doroczne europejskie sympozjum poświęcone algorytmom, ESA 2009 , Notatki z wykładów z informatyki, tom. 5757, Springer, s. 554–565, doi : 10.1007/978-3-642-04128-0_50 , ISBN 978-3-642-04127-3 .

Dalsza lektura

Grandoni, F. (2006), „Uwaga o złożoności minimalnego zbioru dominującego”, Journal of Discrete Algorithms , 4 (2): 209–214, CiteSeerX 10.1.1.108.3223 , doi : 10.1016/j.jda.2005.03 0,002 .
Guha, S.; Khuller, S. (1998), „Algorytmy aproksymacji dla połączonych zestawów dominujących” (PDF) , Algorithmica , 20 (4): 374–387, doi : 10.1007/PL00009201 , hdl : 1903/830 , S2CID 1249122 .
Haynes, Teresa W .; Hedetniemi, Stefan; Slater, Peter (1998a), Podstawy dominacji w wykresach , Marcel Dekker, ISBN 0-8247-0033-3 , OCLC 37903553 .
Haynes, Teresa W .; Hedetniemi, Stefan; Slater, Peter (1998b), Domination in Graphs: Advanced Topics , Marcel Dekker, ISBN 0-8247-0034-1 , OCLC 38201061 .
West, Douglas B. (2001), Wprowadzenie do teorii grafów (wyd. 2), Pearson Education .