Diagram decyzyjny z tłumieniem zera

Diagram decyzyjny z pomijaniem zera ( ZSDD lub ZDD ) jest szczególnym rodzajem binarnego diagramu decyzyjnego ( BDD ) ze stałą kolejnością zmiennych. Ta struktura danych zapewnia kanonicznie zwartą reprezentację zbiorów, szczególnie odpowiednią dla niektórych problemów kombinatorycznych . Przypomnij sobie strategię redukcji uporządkowanego binarnego diagramu decyzyjnego (OBDD), tj. węzeł jest zastępowany jednym z jego dzieci, jeśli obie krawędzie zewnętrzne wskazują na ten sam węzeł. W przeciwieństwie do tego, węzeł w ZDD jest zastępowany swoim ujemnym dzieckiem, jeśli jego dodatnia krawędź wskazuje na końcowy węzeł 0. Zapewnia to alternatywną silną postać normalną z ulepszoną kompresją rzadkich zbiorów. Opiera się na zasadzie redukcji opracowanej przez Shin-ichi Minato w 1993 roku.

Tło

Na binarnym diagramie decyzyjnym funkcja boolowska może być reprezentowana jako ukorzeniony, skierowany, acykliczny wykres , który składa się z kilku węzłów decyzyjnych i węzłów końcowych. W 1993 roku Shin-ichi Minato z Japonii zmodyfikował BDD Randala Bryanta w celu rozwiązywania problemów kombinatorycznych . Jego BDD „Zero-Suppressed” mają na celu reprezentowanie i manipulowanie rzadkimi zestawami wektorów bitowych . Jeśli dane problemu są reprezentowane jako wektory bitowe o długości n, to dowolny podzbiór wektorów może być reprezentowany przez funkcję boolowską po n zmiennych dających 1, gdy wektor odpowiadający przypisaniu zmiennej znajduje się w zbiorze.

Według Bryanta możliwe jest użycie form funkcji logicznych do wyrażenia problemów obejmujących sumę produktów. Takie formy są często reprezentowane jako zestawy „kostek”, z których każdy jest oznaczony ciągiem zawierającym symbole 0, 1 i -. Na przykład funkcja ${\ Displaystyle ({\ bar {x}} _ {1} \ ziemi x_ {2}) \ lor ({\ bar {x}}_{2}\oplus x_{3})}$ można zilustrować zbiorem ${\ Displaystyle \ {01-, -11, -00 \}}$ . Używając bitów 10, 01 i 00 do oznaczenia odpowiednio symboli 1, 0 i -, można przedstawić powyższy zestaw za pomocą wektorów bitowych w postaci { 011000 , 001010 , $011000,001010,000101 \}}$ . Zauważ, że zbiór wektorów bitowych jest rzadki, ponieważ liczba wektorów jest mniejsza niż 2 ⁿ , czyli maksymalna liczba wektorów bitowych, a zbiór zawiera wiele elementów równych zeru. W takim przypadku węzeł można pominąć, jeśli ustawienie zmiennej węzła na 1 powoduje, że funkcja daje 0. Jest to widoczne w warunku, że 1 na jakiejś pozycji bitowej oznacza, że wektora nie ma w zbiorze. W przypadku zbiorów rzadkich ten warunek jest powszechny, a zatem możliwych jest wiele eliminacji węzłów.

Minato udowodnił, że ZDD są szczególnie odpowiednie dla problemów kombinatorycznych , takich jak klasyczne problemy minimalizacji logiki dwupoziomowej , problem trasy skoczka , symulacja błędów, analiza czasu, problem N-królowych , a także słaby podział. Używając ZDD, można zmniejszyć rozmiar reprezentacji zestawu n-bitowych wektorów w OBDD co najwyżej o współczynnik n. W praktyce optymalizacja jest istotna statystycznie .

Definicje

Diagram decyzyjny z tłumieniem zera (ZDD) definiujemy jako dowolny skierowany graf acykliczny taki, że:

1. Węzłem końcowym jest:

Specjalny ⊤ węzeł, który reprezentuje rodzinę jednostek $)$ tj zbiór lub
Specjalny węzeł ⊥ reprezentujący pustą rodzinę ${\ displaystyle \ emptyset}$ .

2. Każdy węzeł nieterminalny spełnia następujące warunki

: Węzeł jest oznaczony dodatnią liczbą całkowitą v. Ta etykieta nie musi być unikalna.

B. Węzeł ma stopień wyjściowy równy 2. Jedna z wychodzących krawędzi nosi nazwę „LO”, a druga „HI”. (Na diagramach można narysować linie przerywane dla krawędzi LO i linie ciągłe dla krawędzi HI)

c. Węzeł docelowy jest albo końcowy, albo oznaczony liczbą całkowitą ściśle większą niż v. W ten sposób można pominąć groty strzałek na diagramach, ponieważ kierunki krawędzi można wywnioskować z etykiet.

D. Krawędź HI nigdy nie wskazuje na węzeł ⊥.

3. Istnieje dokładnie jeden węzeł z zerowym stopniem — węzeł główny. Węzeł główny jest końcowy lub oznaczony najmniejszą liczbą całkowitą na diagramie.

4. Jeśli dwa węzły mają tę samą etykietę, to ich krawędzie LO lub HI wskazują różne węzły. Innymi słowy, nie ma zbędnych węzłów.

Nazywamy Z niezredukowanym ZDD, jeśli krawędź HI wskazuje na węzeł ⊥ lub warunek 4 nie jest spełniony. W programach komputerowych funkcje boolowskie można wyrazić w bitach, więc węzeł ⊤ i węzeł ⊥ mogą być reprezentowane przez 1 i 0. Na podstawie powyższej definicji możemy wydajnie reprezentować zbiory kombinacji, stosując dwie reguły do BDD:

1. Wyeliminuj wszystkie węzły, których krawędź 1 wskazuje na węzeł 0-końcowy (Rysunek 1). Następnie połącz krawędź bezpośrednio z innym podgrafem.

2. Udostępnij wszystkie równoważne podwykresy tak samo, jak w przypadku oryginalnych BDD.

Jeśli liczba i kolejność zmiennych wejściowych są stałe, BDD z supresją zerową reprezentuje funkcję boolowską w unikalny sposób (jak pokazano na rysunku 2, możliwe jest użycie BDD do przedstawienia binarnego drzewa boolowskiego).

Reprezentowanie rodziny zbiorów

Niech F będzie ZDD. Niech v będzie jego węzłem głównym. Następnie:

1. Jeśli v = ⊥ , to nie może być innych węzłów, a F reprezentuje Ø, pustą rodzinę.

2. Jeśli v = ⊤, to nie może być innych węzłów, a F reprezentuje rodzinę zawierającą tylko zbiór pusty { Ø }. Nazywamy to rodziną jednostek i oznaczamy ją przez .

3. Jeśli v ma dwoje dzieci. Niech v0 będzie węzłem LO, a v1 węzłem HI. Niech Fi będzie rodziną reprezentowaną przez ZDD zakorzenioną w vi, co można wykazać za pomocą dowodu indukcji. Wtedy F reprezentuje rodzinę

{\ Displaystyle F_ {0} \ kubek \ {\ alfa \ kubek \ {v \} \ środkowy \ alfa \ w F_ {1} \}}

Gałąź LO można przedstawić jako zbiory w F, które nie zawierają v : ${\ Displaystyle F_ {0} = \ {\ alfa: \ alfa \ w F, v\notin \alpha \}}$

A gałąź HI jako zbiory w F, które zawierają v : ${\ Displaystyle F_ {1} = \ {\ alfa \ ukośnik odwrotny \ {v \ }:\alpha \in F,v\in \alpha \}}$

Przykład

Rysunek 3
Rysunek 4
Rysunek 5
Rysunek 6

Rysunek 3: Rodzina ${\ Displaystyle \ pusty zestaw \ kubek \ {\ pusty zestaw \ kubek \ {2 \} \} = \ {\ {2 \} \} }$ . Możemy to $elementarną$ . Rodziny elementarne składają się z formy i są oznaczone przez $\ displaystyle$ $}$ n

Rysunek 4: Rodzina ${\ Displaystyle \ {\ pusty zestaw \} \ kubek \ {\ pusty zestaw \ kubek \ {2 \} \} = \ {\pusty zbiór,\{2\}\}}$

Rysunek 5: Rodzina ${\ Displaystyle \ {\ {2 \} \} \ kubek \ {\ pusty zestaw \ kubek \ { 1\}\}=\{\{1\},\{2\}\}}$

Rysunek 6: Rodzina ${\ Displaystyle \ {\ {1 \} \ kubek \ {2 \} \} = \ {\ {1,2 \ }\}}$

Cechy

Jedną z cech ZDD jest to, że forma nie zależy od liczby zmiennych wejściowych, o ile zestawy kombinacji są takie same. Nie ma potrzeby ustalania liczby zmiennych wejściowych przed wygenerowaniem wykresów. ZDD automatycznie pomijają zmienne dla obiektów, które nigdy nie pojawiają się w kombinacji, stąd efektywność manipulowania rzadkimi kombinacjami. Kolejną zaletą ZDD jest to, że liczba ścieżek 1 na grafie jest dokładnie równa liczbie elementów w zbiorze kombinacji. W oryginalnych BDD eliminacja węzła łamie tę właściwość. Dlatego ZDD są lepsze niż proste BDD do reprezentowania zestawów kombinacji. Jednak lepiej jest używać oryginalnych BDD do reprezentowania zwykłych funkcji boolowskich, jak pokazano na rysunku 7.

Rysunek 7: Manipulowanie bitami i podstawowe operacje. Rysunek 8: Tłumienie nieistotnych zmiennych

Podstawowe operacje

Tutaj mamy podstawowe operacje dla ZDD, ponieważ różnią się one nieco od tych z oryginalnych BDD. Przykłady wygenerowane z poniższej tabeli można znaleźć na rysunku 8.

Empty() zwraca ř (pusty zbiór)

Base() zwraca{0}

Podzbiór1(P, var) zwraca podzbiór P, na przykład var = 1

Podzbiór0(P, var) zwraca podzbiór P, na przykład var = 0

Change( P, var) zwraca P, gdy var jest odwrócone

Union (P, Q) zwraca (

{\ Displaystyle P \ puchar Q}

)

Intsec (P, Q) zwraca (

{\ Displaystyle P \ cap Q}

)

Różn.(P, Q) zwraca (

{\ Displaystyle PQ}

)

Count (P) zwraca

{\ Displaystyle \ lewo \ vert P \ prawo \ vert}

. (liczba elementów)

W ZDD nie ma operacji NOT, która jest podstawową operacją w oryginalnych BDD. Powodem jest to, że zbioru dopełniacza $nie$ $można$ bez zdefiniowania . W ZDD $.$ obliczyć jako Diff (U, P

Algorytmy

Załóżmy ${\ Displaystyle \ lewo \ vert P \ right \ vert = \ lewo \ vert P_ {0} \ right \ vert + \ lewo \ vert P_ {1} \ right \ vert } , możemy rekurencyjnie obliczyć liczbę zestawów$ w a ZDD, dzięki czemu udało nam się 34. wyznaczyć 54-osobową rodzinę. Dostęp swobodny jest szybki, a każda możliwa operacja dla tablicy zestawów może być wydajnie wykonywana na ZDD.

Według Minato, powyższe operacje dla ZDD mogą być wykonywane rekurencyjnie, tak jak oryginalne BDD. Aby w prosty sposób opisać algorytmy, zdefiniujemy procedurę Getnode(top, P0, P1) , która zwraca węzeł dla zmiennej top i dwóch podgrafów P0 i P1. Możemy użyć tablicy mieszającej, zwanej tabelą uniq, aby każdy węzeł był unikalny. Eliminacja i udostępnianie węzłów jest zarządzane tylko przez Getnode() .

Getnode (top, P0, P1) { if (P1 == ø) return P0; /* eliminacja węzła */ P = wyszukaj węzeł z (top, P0, P1 ) w tabeli uniq; jeśli (P istnieje) zwróć P; /* udostępnianie węzłów */ P = generowanie węzła z (top, P0, P1 ); dołącz P do tabeli uniq; powrót P; }

Używając Getnode() , możemy następnie przedstawić inne podstawowe operacje w następujący sposób:

 Podzbiór1 (P, var) { if (P.top < var) return ø; jeśli (P.top == var) zwróć P1;  if (P.top > var) return Getnode (P.top, Subset1(P0, var), Subset1(P1, var));  }

 Podzbiór0 (P, var) { if (P.top < var) return ø; jeśli (P.top == var) zwróć P0;  if (P.top > var) return Getnode (P.top, Subset0(P0, var), Subset0(P1, var));  }

 Zmień (P, var) { if (P.top < var) return Getnode (var, ø, P); if (P.top == var) zwróć Getnode (var, P1, P0);  if (P.top > var) return Getnode (P.top, Change(P0, var), Change(P1, var));  } Suma (P, Q) { jeśli (P == ø) powrót Q;  jeśli (Q == ø) zwróć P;  jeśli (P == Q) zwróć P;  if (P.top > Q.top) zwróć Getnode (P.top, Union(P0, Q), P1);  if (P.top < Q.top) return Getnode (Q.top, Union(P, Q0), Q1);  if (P.top == Q.top) return Getnode (P.top, Union(P0, Q0), Union(P1, Q1));  }

 Intsec (P, Q) { jeśli (P == ø) return ø; jeśli (Q == ø) zwróć ø;  jeśli (P == Q) zwróć P;  if (P.top > Q.top) return Intsec(P0, Q);  jeśli (P.top < Q.top) zwróć Intsec (P, Q0);  if (P.top == Q.top) return Getnode (P.top, Intsec(P0, Q0), Intsec(P1, Q1));  }

 Różn. (P, Q) { jeśli (P == ø) zwróć ø; jeśli (Q == ø) zwróć P;  jeśli (P == Q) zwróć ø;  if (P.top > Q.top) zwróć Getnode(P.top, Diff(P0, Q), P1;) if (P.top < Q.top) zwróć Diff(P, Q0);  if (P.top == Q.top) return Getnode (P.top, Diff(P0, Q0), Diff(P1, Q1));  }

 Policz (P) { jeśli (P == ø) zwróć 0; jeśli (P == {ø}) zwróć 1;  return Liczba(P0) + Liczba(P1);  }

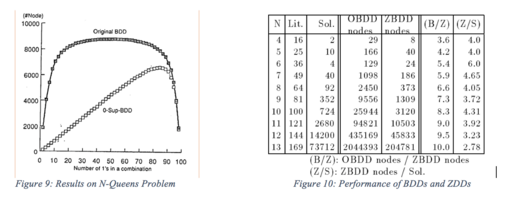
Algorytmy te w najgorszym przypadku zajmują wykładniczy czas dla liczby zmiennych; możemy jednak poprawić wydajność, używając pamięci podręcznej, która zapamiętuje wyniki ostatnich operacji w podobny sposób w BDD. Pamięć podręczna zapobiega zduplikowanym wykonaniom dla równoważnych wykresów podrzędnych. Bez żadnych duplikatów algorytmy mogą działać w czasie proporcjonalnym do wielkości wykresów, jak pokazano na rysunku 9 i 10.

Rysunek 9: Wyniki problemu N-Queens Rysunek 10: Wydajność ZDD w porównaniu z wydajnością BDD

Aplikacja

ZDD jako słowniki

ZDD mogą być używane do reprezentowania pięcioliterowych słów języka angielskiego, na przykład zestawu WORDS (o rozmiarze 5757) ze Stanford GraphBase . $na$ jest rozważenie funkcji , tylko jeśli pięć liczb ${\ Displaystyle (x_ {1}, ..., x_ {5}) _ {2}$ , ${\ Displaystyle (x_ {6}, ..., x_ {10}) _$ ${\ Displaystyle (x_ {21}, ..., x_ {25}) _ {2}}$ , kodują litery angielskiego słowa, gdzie za $\ Displaystyle a = (00001) _ {2}}$ , ..., ${\ Displaystyle z = (11010) _ {2}}$ . Na ${\ Displaystyle f (0,0,1,1,1,0,1,1,1,1,0,1,1,1,1,0,0,1,1,0,1,1 ,0,0,x_{25})=x_{25}}$ . Funkcja 25 zmiennych ma Z(f) = 6233 wierzchołków – co nie jest takie złe jak na reprezentację 5757 słów. W porównaniu z drzewami binarnymi , próbami lub tabelami mieszającymi , ZDD może nie być najlepszym narzędziem do wykonywania prostych wyszukiwań, ale jest skuteczne w wyszukiwaniu danych, które są tylko częściowo określone lub danych, które mają pasować do klucza tylko w przybliżeniu. Złożone zapytania można łatwo obsłużyć. Ponadto ZDD nie obejmują tak wielu zmiennych. W rzeczywistości, używając ZDD, można przedstawić te pięcioliterowe słowa jako funkcję ${5})}$ $\ Displaystyle F (a_ {1}, ..., z_ {1}, a_ {2}, ..., z_ {2}, ..., a_ {5},...,$ $z_$ , który ma 26 × 5 = 130 zmiennych, gdzie na przykład zmienna określa, czy drugą literą jest „a Aby przedstawić słowo „szalony”, można uczynić F prawdziwym, gdy ${\ Displaystyle c_ {1}= r_ {2} = a_ {3} = z_ {4} = y_ {5} = 1},$ a wszystkie inne zmienne wynoszą 0. Zatem F można uznać za rodzinę składającą się z 5757 podzbiory ${\ Displaystyle \ {w_ {1}, h_ {2}, i_ {3}, c_ {4}, h_ {5} \}}$ , itd. Przy tych 130 zmiennych rozmiar ZDD Z(F) wynosi w rzeczywistości 5020 zamiast 6233. Według Knutha, równoważny rozmiar B(F) przy użyciu BDD wynosi 46189 - znacznie większy niż Z(F). Pomimo posiadania podobnych teorii i algorytmów, ZDD przewyższają BDD w tym problemie z dość dużym marginesem. W konsekwencji ZDD pozwalają nam wykonywać pewne zapytania, które są zbyt uciążliwe dla BDD. Złożone rodziny podzbiorów można łatwo zbudować z rodzin elementarnych. Aby wyszukać słowa zawierające określony wzór, można użyć algebry rodziny na ZDD do obliczenia ${\ Displaystyle (F / P) \ sqcup P}$ , gdzie P jest wzorem, np. ${\ Displaystyle a_ {1} \ sqcup h_ {3} \ sqcup e_ {5}}$ .

Rysunek 11: siatka trzy na trzy

ZDD do reprezentowania prostych ścieżek

Można użyć ZDD do przedstawienia prostych ścieżek w grafie nieskierowanym . Na przykład istnieje 12 sposobów, aby przejść z lewego górnego rogu siatki trzy na trzy (pokazanej na rysunku 11) do prawego dolnego rogu, nie odwiedzając żadnego punktu dwa razy.

Rysunek 12: 12 możliwych ścieżek prowadzących z jednego rogu do drugiego ukośnego rogu

Ścieżki te mogą być reprezentowane przez ZDD pokazany na rysunku 13, w którym każdy węzeł mn reprezentuje pytanie „czy ścieżka obejmuje łuk między m i n ?” Na przykład gałąź LO między 13 a 12 wskazuje, że jeśli ścieżka nie obejmuje łuku od 1 do 3, następną rzeczą, o którą należy zapytać, jest to, czy zawiera łuk od 1 do 2. Brak gałęzi LO pozostawiając węzeł 12 wskazuje, że każda ścieżka, która nie prowadzi od 1 do 3, musi zatem przejdź od 1 do 2. (Następne pytanie, które należy zadać, dotyczyłoby łuku między 2 a 4). W tym ZDD otrzymujemy pierwszą ścieżkę na rysunku 12, biorąc gałęzie HI w węzłach 13, 36, 68 i 89 ZDD (odgałęzienia LO, które po prostu idą do ⊥ są pomijane). Chociaż ZDD na rysunku 13 może w żaden sposób nie wydawać się znaczący, zalety ZDD stają się oczywiste, gdy siatka się powiększa. Na przykład dla siatki osiem na osiem liczba prostych ścieżek od rogu do rogu wynosi 789 360 053 252 (Knuth). Ścieżki można zilustrować za pomocą 33580 węzłów przy użyciu ZDD.

Rysunek 13: ZDD dla prostych ścieżek siatki trzy na trzy

Prawdziwy przykład prostych ścieżek zaproponował Randal Bryant: „Załóżmy, że chciałbym odbyć samochodową wycieczkę po kontynentalnych Stanach Zjednoczonych, odwiedzając wszystkie stolice stanów i przejeżdżając przez każdy stan tylko raz. Jaką trasę powinienem obrać, aby zminimalizować całkowity dystans?” Rysunek 14 przedstawia nieskierowany wykres dla tej mapy drogowej, gdzie liczby wskazują najkrótsze odległości między sąsiednimi stolicami. Problem polega na wybraniu podzbioru tych krawędzi, które tworzą ścieżkę Hamiltona o najmniejszej całkowitej długości. Każda ścieżka Hamiltona na tym wykresie musi zaczynać się lub kończyć w Augusta, Maine (ME). Załóżmy, że zaczyna się w CA. Można znaleźć ZDD, który charakteryzuje wszystkie ścieżki od CA do ME. Według Knutha, ten ZDD okazuje się mieć tylko 7850 węzłów i faktycznie pokazuje, że możliwe są dokładnie 437 525 772 584 prostych ścieżek z CA do ME. Według liczby krawędzi funkcja generująca to

                       ${\ Displaystyle 4z ^ {11} + 124z ^ {12} + 1539z ^ {13} + ... + 33385461z ^ {46} + 2707075z ^ {47}}$  ;

więc najdłuższe takie ścieżki są hamiltonowskie i mają rozmiar 2 707 075. ZDD w tym przypadku są skuteczne dla prostych ścieżek i ścieżek hamiltonowskich .

Rysunek 14: Nieskierowany wykres stanów kontynentalnych Stanów Zjednoczonych

Problem ośmiu królowych

Zdefiniuj 64 zmienne wejściowe reprezentujące pola na szachownicy. Każda zmienna oznacza obecność lub brak hetmana na tym polu. Rozważ to,

W określonej kolumnie tylko jedna zmienna ma wartość „1”.
W określonym wierszu tylko jedna zmienna ma wartość „1”.
Na określonej przekątnej jedna lub żadna zmienna to „1”.

Chociaż można rozwiązać ten problem, konstruując OBDD, bardziej efektywne jest użycie ZDD. Konstruowanie ZDD dla problemu 8 królowych wymaga 8 kroków od S1 do S8. Każdy krok można zdefiniować w następujący sposób:

S1: Reprezentuje wszystkie możliwości umieszczenia hetmana w pierwszym rzędzie.

S2: Reprezentuje wszystkie wybory umieszczenia hetmana w drugim rzędzie, aby nie naruszać pierwszego hetmana.

S3: Reprezentuje wszystkie wybory umieszczenia hetmana w trzecim rzędzie, tak aby nie naruszał poprzednich hetmanów.

…

S8: Reprezentuje wszystkie wybory umieszczenia hetmana w ósmym rzędzie, tak aby nie naruszał poprzednich hetmanów.

ZDD dla S8 składa się ze wszystkich potencjalnych rozwiązań problemu 8-Queens. W przypadku tego konkretnego problemu buforowanie może znacznie poprawić wydajność algorytmu. Korzystanie z pamięci podręcznej w celu uniknięcia duplikatów może rozwiązać problemy N-Queens nawet 4,5 razy szybciej niż użycie tylko podstawowych operacji (jak zdefiniowano powyżej), pokazanych na rysunku 10.

Problem trasy rycerskiej

Problem trasy rycerskiej ma znaczenie historyczne. Graf rycerza zawiera n2 wierzchołków przedstawiających pola szachownicy. Krawędzie ilustrują legalne ruchy skoczka. Rycerz może odwiedzić każde pole planszy dokładnie raz. Olaf Schröer, M. Löbbing i Ingo Wegener podeszli do tego problemu, a mianowicie na tablicy, przypisując zmienne boolowskie dla każdej krawędzi grafu, w sumie 156 zmiennych do wyznaczenia wszystkich krawędzi. Rozwiązanie problemu można wyrazić za pomocą 156-bitowego wektora kombinowanego. Według Minato konstrukcja ZDD dla wszystkich rozwiązań jest zbyt duża, aby można ją było rozwiązać bezpośrednio. Łatwiej jest dzielić i rządzić. Dzieląc problemy na dwie części planszy i konstruując ZDD w podprzestrzeniach, można rozwiązać problem trasy Rycerza z każdym rozwiązaniem zawierającym 64 krawędzie. Ponieważ jednak wykres nie jest bardzo rzadki, przewaga korzystania z ZDD nie jest tak oczywista.

Symulacja awarii

N. Takahashi i inni zasugerowali metodę symulacji usterek z uwzględnieniem wielu usterek przy użyciu OBDD. Ta dedukcyjna metoda przesyła zestawy błędów z wejść głównych do wyjść głównych i wychwytuje błędy na wyjściach głównych. Ponieważ ta metoda obejmuje wyrażenia z zestawu kostek unate, ZDD są bardziej wydajne. Optymalizacje z ZDD w obliczeniach pojedynczych zestawów kostek wskazują, że ZDD mogą być przydatne w opracowywaniu systemów CAD VLSI oraz w niezliczonych innych zastosowaniach.

Dostępne pakiety

CUDD : Pakiet BDD napisany w C, który implementuje BDD i ZBDD, University of Colorado, Boulder
JDD , biblioteka Java, która implementuje typowe operacje BDD i ZBDD
Graphillion , Implementacja oprogramowania ZDD oparta na Pythonie
[1] , Implementacja CWEB ZDD autorstwa Donalda Knutha.

Dalsza lektura

Minato, Shin-Ichi (1993). „BDDS z tłumieniem zera do manipulacji zbiorami w problemach kombinatorycznych”. Materiały z 30. międzynarodowej konferencji poświęconej automatyzacji projektowania - DAC '93 . s. 272–277. doi : 10.1145/157485.164890 . ISBN 978-0-89791-577-9 . S2CID 11096308 .
Ch. Meinel, T. Theobald, „ Algorytmy i struktury danych w projektowaniu VLSI: OBDD – podstawy i zastosowania” , Springer-Verlag, Berlin, Heidelberg, Nowy Jork, 1998.
Minato, Shin-ichi (maj 2001). „BDD z zerowym tłumieniem i ich zastosowania”. International Journal on Software Tools for Technology Transfer . 3 (2): 156–170. doi : 10.1007/s100090100038 . hdl : 2115/16895 . S2CID 42919336 .
Bryant, RE (1995). „Binarne diagramy decyzyjne i nie tylko: technologie umożliwiające formalną weryfikację”. Materiały z Międzynarodowej Konferencji IEEE na temat Projektowania Wspomaganego Komputerowo (ICCAD) . s. 236–243. doi : 10.1109/ICCAD.1995.480018 . ISBN 978-0-8186-7213-2 . S2CID 62602492 .
Lynn, Ben. „ZDD”. ZDDs - Wprowadzenie, Uniwersytet Stanforda, 2005, crypto.stanford.edu/pbc/notes/zdd/.
Miszczenko, Alan (2001). „Wprowadzenie do binarnych diagramów decyzyjnych z tłumieniem zera” (PDF) . CiteSeerX 10.1.1.67.8986 . S2CID 14216256 . {{ cite journal }} : Cite journal wymaga |journal= ( pomoc )
Knuth, Donald E. Sztuka programowania komputerowego, tom 4. 22 grudnia 2008 r.

Linki zewnętrzne

Lynn, Ben. „ZDD”. ZDDs - Wprowadzenie, Uniwersytet Stanforda, 2005, crypto.stanford.edu/pbc/notes/zdd/
Donald Knuth , Zabawa z binarnymi diagramami decyzyjnymi z tłumieniem zera (ZDD) (wykład wideo, 2008)
Minato Shin-ichi, Liczenie ścieżek na wykresach (podstawy ZDD) (ilustracja wideo wyprodukowana na Miraikan)