trójkąt kataloński

W matematyce kombinatorycznej $X$ kataloński jest trójkątem liczbowym którego wpisy podają liczbę ciągów składających się z n k Y , że żaden początkowy nie ma więcej Y niż X. Jest to uogólnienie liczb katalońskich i nosi imię Eugène Charles Catalan . Bailey pokazuje, że spełniają następujące właściwości: do ${\ Displaystyle C (n, k)$

1. ${\ Displaystyle C (n, 0) = 1 {\ tekst {dla}} n \ geq 0}$ .
2. ${\ Displaystyle C (n, 1) = n {\ tekst {dla}} n \ geq 1}$ .
3. ${\ Displaystyle C (n + 1, k) = C (n + 1,k-1)+C(n,k){\text{ dla }}1<k<n+1}$
4. ${\ Displaystyle C (n + 1, n + 1) = C (n + 1, n) {\ tekst {dla }}n\geq 1}$ .

Wzór 3 pokazuje, że wpis w trójkącie uzyskuje się rekurencyjnie przez dodanie liczb z lewej strony i powyżej trójkąta. Najwcześniejsze pojawienie się trójkąta katalońskiego wraz ze wzorem rekurencji znajduje się na stronie 214 traktatu o rachunku różniczkowym opublikowanego w 1800 roku przez Louisa François Antoine'a Arbogasta .

Shapiro wprowadza inny trójkąt, który nazywa trójkątem katalońskim, różniącym się od omawianego tutaj trójkąta.

Ogólna formuła

Ogólny wzór na do $\ Displaystyle C (n, k)}$ jest podany przez

${\ Displaystyle C (n, k) = {\ binom {n + k} {k}} - {\ binom {n +k}{k-1}}}$

Więc

${\ Displaystyle C (n, k) = {\ Frac {nk + 1} {n + 1}} {\ binom {n+k}{k}}}$

Kiedy ${\ displaystyle k = n}$ , przekątna do ( n , n ) jest n -tą liczbą katalońską .

Suma wierszy n -tego wiersza to ( n + 1) -ta liczba katalońska , przy użyciu tożsamości kija hokejowego i alternatywnego wyrażenia dla liczb katalońskich.

Niektóre wartości są podane przez

k N	0	1	2	3	4	5	6	7	8
0	1
1	1	1
2	1	2	2
3	1	3	5	5
4	1	4	9	14	14
5	1	5	14	28	42	42
6	1	6	20	48	90	132	132
7	1	7	27	75	165	297	429	429
8	1	8	35	110	275	572	1001	1430	1430

Kombinatoryczna interpretacja -tej wartości $że$ liczba niemalejących partycji z dokładnie n częściami z maksymalną częścią jest mniejsza równa jego indeksowi. Na przykład liczy się ${\ Displaystyle (4,2) = 9}$

${\ Displaystyle 1111,1112,1113,1122,1123,1133,1222,1223,1233}$

Uogólnienie

Trapezy katalońskie to policzalny zbiór trapezów liczbowych, które uogólniają trójkąt kataloński. Trapez kataloński rzędu m = , ... 1 , $.$ to trapez liczbowy, którego wpisy ciągów składających się n oraz k Y tak, że w każdym początkowym segmencie łańcucha liczba Y nie przekracza liczby X o m lub więcej. Z definicji trapez kataloński rzędu m = 1 to trójkąt kataloński, tj. ${\ Displaystyle C_ {1} (n, k) = C (n, k)}$ .

Niektóre wartości katalońskiego trapezu rzędu m = 2 są podane przez

k N	0	1	2	3	4	5	6	7	8
0	1	1
1	1	2	2
2	1	3	5	5
3	1	4	9	14	14
4	1	5	14	28	42	42
5	1	6	20	48	90	132	132
6	1	7	27	75	165	297	429	429
7	1	8	35	110	275	572	1001	1430	1430

Niektóre wartości katalońskiego trapezu rzędu m = 3 są podane przez

k N	0	1	2	3	4	5	6	7	8	9
0	1	1	1
1	1	2	3	3
2	1	3	6	9	9
3	1	4	10	19	28	28
4	1	5	15	34	62	90	90
5	1	6	21	55	117	207	297	297
6	1	7	28	83	200	407	704	1001	1001
7	1	8	36	119	319	726	1430	2431	3432	3432

Ponownie, każdy element jest sumą elementu powyżej i elementu po lewej stronie.

Ogólny wzór na $\ Displaystyle C_ {m} (n, k)}$ jest podany przez

${\ Displaystyle C_ {m} (n, k) = {\ rozpocząć {przypadki} \ lewo ({\ rozpocząć {tablica} {c} n + k \\ k \ koniec {tablica}} \ prawej) & \, \ ,\,0\leq k<m\\\\\left({\begin{tablica}{c}n+k\\k\end{tablica}}\right)-\left({\begin{tablica} {c}n+k\\km\end{tablica}}\right)&\,\,\,m\równoważnik k\równoważnik n+m-1\\\\0&\,\,\,k>n +m-1\end{przypadki}}}$

( n = 0, 1, 2, ... , k = 0, 1, 2, ... , m = 1, 2, 3, ... ).

Dowody ogólnego wzoru na ${\ Displaystyle C_ {m} (n, k)}$

Dowód 1

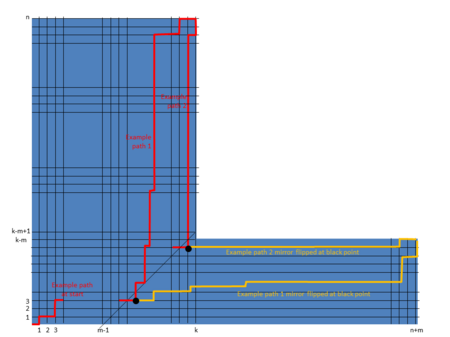
Dowód ten obejmuje rozszerzenie metody Andres Reflection zastosowanej w drugim dowodzie dla liczby katalońskiej na różne przekątne. Poniżej pokazano $(k, n)}$ jak każda ścieżka od lewego dolnego rogu do prawego górnego rogu $) {\$ który przecina ograniczenie ${\ Displaystyle nk + m-1 = 0}$ można również odzwierciedlić w punkcie końcowym ${\ Displaystyle (n + m, km)}$ .

Rozważamy trzy przypadki, aby określić liczbę ścieżek od ${\ Displaystyle (0,0)}$ do ${\ Displaystyle (k, n)}$ , które nie przekraczają ograniczenia: ( , ) {\ Displaystyle (0,0)}

(1) kiedy ograniczenia nie można przekroczyć, więc wszystkie ścieżki od $do$$\ Displaystyle (0,0)}$ , $(k, n) }$ są ważne, tj. do ${\ Displaystyle C_ {m} (n, k) = \ lewo ({\ rozpocząć {tablica} {c} n + k \\$ .

(2) gdy niemożliwe $=$ utworzenie ścieżki, która nie przecina ograniczenia ${ m}(n,k)=0}$ .

(3) kiedy ${\ Displaystyle m \ równoważnik k \ równoważnik n + m-1}$${\ Displaystyle C_ {m} (n, k)}$ wtedy do to liczba „czerwonych” ścieżek $($ o liczbę „ żółte ścieżki, które przekraczają ograniczenie, tj. ${\ Displaystyle \ lewo ({\ rozpocząć {tablica}} {c} ( n+m)+(km)\\km\end{array}}\right)=\left({\begin{array}{c}n+k\\km\end{array}}\right)}$ .

Dlatego liczba ścieżek od ${\ Displaystyle (0,0)}$ do ${\ Displaystyle (k, n)}$ , które nie przekraczają ograniczenia ${\ Displaystyle n-k+m-1=0}$ jest takie, jak wskazano we wzorze w poprzedniej sekcji „ Uogólnienie ”.

Dowód 2

Po pierwsze, potwierdzamy ważność relacji powtarzalności ${\ Displaystyle C_ {m} (n, k) = C_ {m} (n-1, k) + C_ {m} (n, k-1)}$ przez podzielenie na dwie części $\ Displaystyle C_ {m} (n, k)}$ , pierwsza dla kombinacji XY kończących się na X, a druga dla kombinacji kończących się na Y. Pierwsza grupa ma zatem prawidłowe kombinacje i do $}$ drugi ma do ${\ Displaystyle C_ {m} (n, k-1)$ . Dowód 2 kończy się sprawdzeniem ${\ Displaystyle C_ {m} (0,k)}$ czy rozwiązanie spełnia relację powtarzania i spełnia warunki początkowe dla ${\ Displaystyle C_ {m} (n, 0)}$ i do .