Ścieżka Dubinsa

W geometrii termin ścieżka Dubinsa zwykle odnosi się do najkrótszej krzywej, która łączy dwa punkty na dwuwymiarowej płaszczyźnie euklidesowej ( tj. założenie, że pojazd poruszający się po ścieżce może jechać tylko do przodu. Jeśli pojazd może również jechać do tyłu, to ścieżka biegnie po krzywej Reedsa-Sheppa.

W 1957 roku Lester Eli Dubins (1920–2010) udowodnił za pomocą narzędzi analitycznych, że każda taka ścieżka będzie składać się z odcinków o maksymalnej krzywiźnie i / lub prostych. Innymi słowy, najkrótsza ścieżka zostanie utworzona przez połączenie łuków kołowych o maksymalnej krzywiźnie i linii prostych.

W 1974 roku Harold H. Johnson udowodnił wynik Dubinsa, stosując zasadę maksimum Pontriagina . W szczególności Harold H. Johnson przedstawił warunki konieczne i wystarczające, aby krzywa płaska, która ma ograniczoną fragmentarycznie ciągłą krzywiznę oraz określone punkty i kierunki początkowe i końcowe, miała minimalną długość. W 1992 roku ten sam wynik został ponownie pokazany przy użyciu zasady maksimum Pontryagina . Niedawno J. Ayala, D. Kirszenblat i J. Hyam Rubinstein przedstawili dowód z teorii krzywej geometrycznej. Dowód charakteryzujący ścieżki Dubinsa w klasach homotopii podał J. Ayala.

Ścieżka Dubinsa jest powszechnie stosowana w dziedzinie robotyki i teorii sterowania jako sposób planowania ścieżek dla robotów kołowych, samolotów i pojazdów podwodnych. Istnieją proste geometryczne i analityczne metody obliczania optymalnej ścieżki.

Na przykład w przypadku robota kołowego prosty kinematyczny model samochodu (znany również jako samochód Dubinsa) dla systemów to:

$${\ Displaystyle {\ rozpocząć {wyrównane}} {\ kropka {x}} i = V \ cos (\ teta) \\ { \dot {y}}&=V\sin(\theta )\\{\kropka {\theta}}&=u\end{wyrównane}}}$$

gdzie ${\ Displaystyle (x, y)}$ to pozycja samochodu, to $θ$ , samochód porusza się ze stałą prędkością , a prędkość skrętu jest $\ displaystyle \ theta}$ kontrola $ograniczona$ . W tym przypadku maksymalna prędkość skrętu odpowiada pewnemu minimalnemu promieniowi skrętu (i odpowiednio maksymalnej krzywiźnie). Wyznaczone styczne początkowe i końcowe odpowiadają nagłówkom początkowym i końcowym . Ścieżka Dubinsa daje najkrótszą drogę łączącą dwa zorientowane punkty, jaka jest możliwa dla modelu robota kołowego.

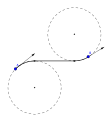
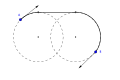
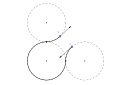
Optymalny typ ścieżki można opisać za pomocą analogii z samochodami wykonującymi „skręt w prawo (R)”, „skręt w lewo (L)” lub jazdę „na wprost (S).” Optymalną ścieżką zawsze będzie co najmniej jeden z sześciu typów: RSR, RSL, LSR, LSL, RLR, LRL. Weźmy na przykład pod uwagę, że dla pewnych określonych pozycji początkowych i końcowych oraz stycznych, optymalna ścieżka jest typu „RSR”. Odpowiada to łukowi skrętu w prawo (R), po którym następuje odcinek linii prostej (S), po którym następuje kolejny łuk skrętu w prawo (R). Poruszanie się wzdłuż każdego segmentu w tej sekwencji na odpowiednią długość utworzy najkrótszą krzywą, która łączy punkt początkowy A z punktem końcowym B z żądanymi stycznymi w każdym punkcie końcowym i która nie przekracza podanej krzywizny.

• 

  Ścieżka RSL Dubins

• 

  Ścieżka RSR Dubins

• 

  Ścieżka LRL Dubins

Problem interwału Dubinsa

Problem interwału Dubinsa jest kluczowym wariantem problemu ścieżki Dubinsa, w którym interwał kierunków kierunków jest określony w punktach początkowych i końcowych. Kierunek stycznej ścieżki w punktach początkowym i końcowym jest ograniczony do tego, aby mieścił się w określonych odstępach. Można to rozwiązać za pomocą analizy geometrycznej lub zasady minimum Pontriagina.

Linki zewnętrzne

• Krzywe Dubinsa z algorytmów planowania autorstwa Stevena M. LaValle'a
• Izochrony dla samochodu Dubins , demonstracja z Wolfram Demonstrations Project