Teoria sterowania

Teoria sterowania to dziedzina inżynierii sterowania i matematyki stosowanej, która zajmuje się sterowaniem systemami dynamicznymi w inżynieryjnych procesach i maszynach. Celem jest opracowanie modelu lub algorytmu regulującego stosowanie danych wejściowych systemu w celu doprowadzenia systemu do pożądanego stanu, przy jednoczesnej minimalizacji opóźnień , przeregulowań lub błędów stanu ustalonego oraz zapewnieniu poziomu stabilności sterowania ; często w celu osiągnięcia pewnego stopnia optymalności .

W tym celu wymagany jest kontroler z wymaganym zachowaniem korygującym. Ten regulator monitoruje sterowaną zmienną procesową (PV) i porównuje ją z wartością odniesienia lub wartością zadaną (SP). Różnica między rzeczywistą a pożądaną wartością zmiennej procesowej, zwana błędu lub błędem SP-PV, jest stosowana jako sprzężenie zwrotne w celu wygenerowania działania sterującego w celu doprowadzenia regulowanej zmiennej procesowej do tej samej wartości, co wartość zadana. Inne badane aspekty to sterowalność i obserwowalność . Teoria sterowania jest wykorzystywana w inżynierii systemów sterowania do projektowania automatyzacji, która zrewolucjonizowała produkcję, samoloty, komunikację i inne gałęzie przemysłu oraz stworzyła nowe dziedziny, takie jak robotyka .

Powszechnie używany jest zwykle schematyczny styl znany jako schemat blokowy . W nim funkcja przenoszenia , zwana także funkcją systemową lub funkcją sieciową, jest matematycznym modelem relacji między wejściem a wyjściem opartym na równaniach różniczkowych opisujących system.

Teoria sterowania sięga XIX wieku, kiedy to teoretyczne podstawy działania zarządców po raz pierwszy opisał James Clerk Maxwell . Teoria sterowania została dalej rozwinięta przez Edwarda Routha w 1874 r., Charlesa Sturma iw 1895 r. Adolfa Hurwitza , którzy wszyscy przyczynili się do ustanowienia kryteriów stabilności sterowania; a od 1922 r. rozwój regulacji PID przez Nicolasa Minorsky'ego . Chociaż głównym zastosowaniem matematycznej teorii sterowania jest inżynieria systemów sterowania , która zajmuje się projektowaniem systemów sterowania procesami dla przemysłu, inne zastosowania wykraczają daleko poza to. Jako ogólna teoria systemów ze sprzężeniem zwrotnym, teoria sterowania jest przydatna wszędzie tam, gdzie występuje sprzężenie zwrotne – dlatego teoria sterowania ma również zastosowanie w naukach przyrodniczych, inżynierii komputerowej, socjologii i badaniach operacyjnych .

Historia

Gubernator odśrodkowy w silniku Boulton & Watt z 1788 roku

Chociaż systemy sterowania różnych typów sięgają starożytności, bardziej formalną analizę dziedziny rozpoczęto od analizy dynamiki regulatora odśrodkowego , przeprowadzonej przez fizyka Jamesa Clerka Maxwella w 1868 r., zatytułowanej On Governors . Regulator odśrodkowy był już używany do regulacji prędkości wiatraków. Maxwell opisał i przeanalizował zjawisko samooscylacji , w którym opóźnienia w systemie mogą prowadzić do nadmiernej kompensacji i niestabilnego zachowania. Wywołało to lawinę zainteresowania tematem, podczas którego kolega z klasy Maxwella, Edward John Routh , wyabstrahował wyniki Maxwella dla ogólnej klasy układów liniowych. Niezależnie Adolf Hurwitz przeanalizował stabilność systemu za pomocą równań różniczkowych w 1877 r., W wyniku czego powstało to, co jest obecnie znane jako twierdzenie Routha – Hurwitza .

Godne uwagi zastosowanie kontroli dynamicznej miało miejsce w obszarze lotów załogowych. Bracia Wright wykonali swoje pierwsze udane loty testowe 17 grudnia 1903 roku i wyróżniali się zdolnością do kontrolowania swoich lotów przez znaczne okresy czasu (bardziej niż zdolność do wytwarzania siły nośnej z płata, która była znana). Ciągła, niezawodna kontrola nad samolotem była konieczna w przypadku lotów trwających dłużej niż kilka sekund.

Do II wojny światowej teoria sterowania stała się ważnym obszarem badań. Irmgard Flügge-Lotz opracowała teorię nieciągłych systemów automatycznego sterowania i zastosowała zasadę bang-bang do rozwoju urządzeń automatycznego sterowania lotem dla samolotów. Inne obszary zastosowania kontroli nieciągłych obejmowały systemy kierowania ogniem , systemy naprowadzania i elektronikę .

Czasami stosuje się metody mechaniczne w celu poprawy stabilności systemów. Na przykład stabilizatory statków to płetwy zamontowane pod linią wody i wyłaniające się z boku. We współczesnych statkach mogą to być sterowane żyroskopowo aktywne płetwy, które mają zdolność zmiany kąta natarcia, aby przeciwdziałać przechyleniom powodowanym przez wiatr lub fale działające na statek.

Wyścig kosmiczny zależał również od dokładnego sterowania statkiem kosmicznym, a teoria sterowania jest również coraz częściej wykorzystywana w takich dziedzinach, jak ekonomia i sztuczna inteligencja. Tutaj można powiedzieć, że celem jest znalezienie modelu wewnętrznego , który jest zgodny z twierdzeniem o dobrym regulatorze . Na przykład w ekonomii im dokładniej model handlu (akcjami lub towarami) przedstawia działania rynku, tym łatwiej może on kontrolować ten rynek (i wydobywać z niego „użyteczną pracę” (zyski). W AI przykładem może być chatbot modelujący stan dyskursu ludzi: im dokładniej potrafi modelować stan człowieka (np. na telefonicznej infolinii wsparcia głosowego), tym lepiej potrafi manipulować człowiekiem (np. w celu wykonania działań naprawczych rozwiązać problem, który spowodował telefon na infolinię). Te dwa ostatnie przykłady przyjmują wąską historyczną interpretację teorii sterowania jako zestawu równań różniczkowych modelujących i regulujących ruch kinetyczny i rozszerzają ją do szerokiego uogólnienia interakcji regulatora z rośliną .

Sterowanie w pętli otwartej i pętli zamkniętej (sprzężenie zwrotne).

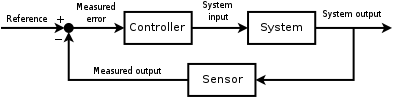
Schemat blokowy systemu sterowania z ujemnym sprzężeniem zwrotnym wykorzystującego pętlę sprzężenia zwrotnego do sterowania zmienną procesową poprzez porównanie jej z żądaną wartością i zastosowanie różnicy jako sygnału błędu do wygenerowania wyjścia sterującego w celu zmniejszenia lub wyeliminowania błędu.

Przykład pojedynczej przemysłowej pętli sterowania; pokazujący stale modulowaną kontrolę przepływu procesu.

Zasadniczo istnieją dwa rodzaje pętli sterowania: sterowanie w pętli otwartej i sterowanie w pętli zamkniętej (sprzężenie zwrotne).

W sterowaniu w otwartej pętli działanie regulacyjne ze strony regulatora jest niezależne od „wyjścia procesowego” (lub „regulowanej zmiennej procesowej” – PV). Dobrym tego przykładem jest kocioł centralnego ogrzewania sterowany tylko zegarem, dzięki czemu ciepło jest dostarczane przez stały czas, niezależnie od temperatury budynku. Akcją regulacyjną jest czasowe włączanie/wyłączanie kotła, zmienną procesową jest temperatura budynku, ale żadna z nich nie jest powiązana.

W regulacji w pętli zamkniętej działanie regulacyjne ze strony regulatora jest uzależnione od sprzężenia zwrotnego z procesu w postaci wartości zmiennej procesowej (PV). W przypadku analogii z kotłem obieg zamknięty obejmowałby termostat do porównania temperatury budynku (PV) z temperaturą ustawioną na termostacie (punkt nastawy - SP). Generuje to wyjście regulatora, aby utrzymać żądaną temperaturę w budynku poprzez włączanie i wyłączanie kotła. Dlatego regulator z pętlą zamkniętą ma pętlę sprzężenia zwrotnego, która zapewnia, że sterownik wykonuje działanie sterujące w celu manipulowania zmienną procesową, aby była taka sama jak „wejście odniesienia” lub „wartość zadana”. Z tego powodu kontrolery z zamkniętą pętlą są również nazywane kontrolerami ze sprzężeniem zwrotnym.

Definicja układu sterowania w pętli zamkniętej według British Standard Institution to „układ sterowania posiadający sprzężenie zwrotne monitorowania, przy czym sygnał odchylenia powstały w wyniku tego sprzężenia zwrotnego jest wykorzystywany do sterowania działaniem końcowego elementu sterującego w taki sposób, aby mają tendencję do zmniejszania odchylenia do zera”.

Podobnie; „ System kontroli ze sprzężeniem zwrotnym to system, który ma tendencję do utrzymywania określonej relacji między jedną zmienną systemową a drugą poprzez porównywanie funkcji tych zmiennych i wykorzystywanie różnicy jako środka kontroli”.

Inne przykłady

tempomat samochodowy , który jest urządzeniem przeznaczonym do utrzymywania stałej prędkości pojazdu pożądanej lub zadanej przez kierowcę. Kontroler to tempomat, instalacja to samochód, a system to samochód i tempomat. Dane wyjściowe systemu to prędkość samochodu, a samo sterowanie to położenie przepustnicy silnika, które określa, ile mocy dostarcza silnik.

Prymitywnym sposobem wdrożenia tempomatu jest po prostu zablokowanie położenia przepustnicy, gdy kierowca włącza tempomat. Jeśli jednak tempomat zostanie włączony na odcinku niepłaskiej drogi, samochód będzie jechał wolniej pod górę i szybciej podczas zjeżdżania ze wzniesienia. Ten typ kontrolera nazywany jest kontrolerem z otwartą pętlą, ponieważ nie ma sprzężenia zwrotnego ; żaden pomiar wyjścia systemu (prędkości samochodu) nie jest używany do zmiany sterowania (położenia przepustnicy). W rezultacie sterownik nie może skompensować zmian działających na samochód, takich jak zmiana nachylenia drogi.

W systemie sterowania z zamkniętą pętlą dane z czujnika monitorującego prędkość samochodu (wyjście systemu) wchodzą do sterownika, który w sposób ciągły porównuje wielkość reprezentującą prędkość z wielkością odniesienia reprezentującą żądaną prędkość. Różnica, zwana błędem, określa położenie przepustnicy (sterowanie). Rezultatem jest dopasowanie prędkości samochodu do prędkości odniesienia (utrzymanie pożądanej mocy wyjściowej systemu). Teraz, gdy samochód jedzie pod górę, różnica między wartością wejściową (zmierzoną prędkością) a wartością odniesienia w sposób ciągły określa położenie przepustnicy. Gdy wykrywana prędkość spada poniżej wartości odniesienia, różnica wzrasta, przepustnica otwiera się, a moc silnika wzrasta, przyspieszając pojazd. W ten sposób sterownik dynamicznie przeciwdziała zmianom prędkości samochodu. Główną ideą tych systemów sterowania jest pętla sprzężenia zwrotnego , sterownik wpływa na wyjście systemu, które z kolei jest mierzone i podawane z powrotem do sterownika.

Klasyczna teoria sterowania

Aby przezwyciężyć ograniczenia kontrolera z otwartą pętlą , teoria sterowania wprowadza sprzężenie zwrotne . Sterownik z zamkniętą pętlą wykorzystuje sprzężenie zwrotne do sterowania stanami lub wyjściami systemu dynamicznego . Jego nazwa pochodzi od ścieżki informacyjnej w systemie: wejścia procesowe (np. napięcie przyłożone do silnika elektrycznego ) mają wpływ na wyjścia procesowe (np. prędkość lub moment obrotowy silnika), które są mierzone czujnikami i przetwarzane przez kontroler; wynik (sygnał sterujący) jest „zwracany” jako wejście do procesu, zamykając pętlę.

Sterowniki z zamkniętą pętlą mają następujące zalety w stosunku do kontrolerów z otwartą pętlą :

tłumienie zakłóceń (takich jak wzniesienia w powyższym przykładzie z tempomatem)
gwarantowana wydajność nawet przy niepewności modelu , gdy struktura modelu nie pasuje idealnie do rzeczywistego procesu, a parametry modelu nie są dokładne
niestabilne procesy można ustabilizować
zmniejszona wrażliwość na zmiany parametrów
ulepszona wydajność śledzenia referencji

W niektórych systemach sterowanie w pętli zamkniętej i otwartej jest stosowane jednocześnie. W takich systemach sterowanie w pętli otwartej nazywane jest sprzężeniem zwrotnym i służy do dalszej poprawy wydajności śledzenia odniesienia.

Powszechną architekturą regulatora z zamkniętą pętlą jest regulator PID .

Funkcja przesyłania w pętli zamkniętej

Sygnał wyjściowy systemu y ( t ) jest przekazywany z powrotem przez czujnik pomiarowy F do porównania z wartością odniesienia r ( t ). Kontroler C bierze następnie błąd e (różnica) między wartością zadaną a wyjściem, aby zmienić wejścia u w sterowanym systemie P . Pokazano to na rysunku. Ten rodzaj kontrolera to kontroler z zamkniętą pętlą lub kontroler ze sprzężeniem zwrotnym.

Nazywa się to systemem sterowania z jednym wejściem i jednym wyjściem ( SISO ); Powszechne są systemy MIMO (tzn. Multi-Input-Multi-Output), z więcej niż jednym wejściem/wyjściem. W takich przypadkach zmienne są reprezentowane przez wektory zamiast prostych wartości skalarnych . W przypadku niektórych układów parametrów o rozkładzie wektory mogą być nieskończenie wymiarowe (zazwyczaj funkcje).

Jeśli założymy, że regulator C , instalacja P i czujnik F są liniowe i niezmienne w czasie (tj. elementy ich funkcji przenoszenia C ( s ), P ( s ) i F ( s ) nie zależą od czasu) , powyższe systemy można analizować za pomocą transformaty Laplace'a na zmiennych. Daje to następujące zależności:

{\ Displaystyle Y (s) = P (s) U (s)}

{\ Displaystyle U (s) = do (s)E (s)}

{\ Displaystyle E (s) = R (s) -F (s) Y (s).}

Rozwiązanie dla Y ( s ) pod względem R ( s ) daje

{\ Displaystyle Y (s) = \ lewo ({\ Frac {P (s) C (s)} {1 + P (s) C (s) F (s)}} \ prawej) R (s) = H (s)R(s).}

H. $s)} {1+F(s)P(s)C(s)}}}$ jest określane jako funkcja przenoszenia w zamkniętej pętli systemu. Licznik to wzmocnienie w przód (w otwartej pętli) od r do y , a mianownik to jeden plus zysk w obejściu pętli sprzężenia zwrotnego, tak zwane wzmocnienie pętli. Jeśli ${\ Displaystyle | P (s) C (s) | \ gg 1}$ , tj. ma dużą normę z każdą wartością s , a jeśli ${\ Displaystyle | F (s) | \ około 1}$ , wtedy Y ( s ) jest w przybliżeniu równe R ( s ), a wyjście ściśle podąża za wejściem referencyjnym.

Kontrola sprzężenia zwrotnego PID

Schemat blokowy regulatora PID w pętli sprzężenia zwrotnego,

r (t)

to pożądana wartość procesu lub „wartość zadana”, a

y (t)

to zmierzona wartość procesu.

Regulator proporcjonalno-całkująco-różniczkujący (regulator PID) jest techniką sterowania mechanizmem sprzężenia zwrotnego pętli sterowania, szeroko stosowaną w układach sterowania.

Regulator PID w sposób ciągły oblicza wartość błędu $e (t)$ jako różnicę między żądaną wartością zadaną a mierzoną zmienną procesową i stosuje poprawkę opartą na składnikach proporcjonalnych , całkujących i różniczkujących . PID to skrót od Proportional-Integral-Derivative , odnoszący się do trzech warunków działających na sygnale błędu w celu wytworzenia sygnału sterującego.

Teoretyczne zrozumienie i zastosowanie sięga lat dwudziestych XX wieku i są one wdrażane w prawie wszystkich analogowych systemach sterowania; pierwotnie w sterownikach mechanicznych, a następnie przy użyciu dyskretnej elektroniki, a później w komputerach procesów przemysłowych. Regulator PID jest prawdopodobnie najczęściej używanym projektem sterowania ze sprzężeniem zwrotnym.

Jeśli $u (t)$ jest sygnałem sterującym wysłanym do systemu, $y (t)$ jest zmierzonym wyjściem, a $r (t)$ jest pożądanym wyjściem, a $e (t) = r (t) - y (t)$ jest śledzeniem błąd, regulator PID ma postać ogólną

{\ Displaystyle u (t) = K_ {P} e (t) + K_ {I} \ int ^ {t} e (\ tau) {\ tekst {d}} \ tau + K_ {D} {\ frac { {\text{d}}e(t)}{{\text{d}}t}}.}

$KD , często iteracyjnie przez „strojenie” i przez$ regulację trzech parametrów $KP bez$ , $KI szczególnej$ i znajomości modelu instalacji. Stabilność często można zapewnić tylko za pomocą składnika proporcjonalnego. Składnik całkujący pozwala na odrzucenie zakłócenia skokowego (często uderzająca specyfikacja w sterowaniu procesem ). Termin pochodny jest używany do zapewnienia tłumienia lub kształtowania odpowiedzi. Regulatory PID są najbardziej ugruntowaną klasą systemów sterowania: nie można ich jednak stosować w kilku bardziej skomplikowanych przypadkach, zwłaszcza jeśli rozważa się systemy MIMO .

Zastosowanie transformacji Laplace'a daje w rezultacie przekształcone równanie regulatora PID

{\ Displaystyle u (s) = K_ {P} \, e (s) + K_ {ja }\,{\frac {1}{s}}\,e(s)+K_{D}\,s\,e(s)}

{\ Displaystyle u (s) = \ lewo (K_ {P} + K_ {I} \, {\ Frac {1} {s}} + K_ {D} \, s \ prawo) e (S)}

z funkcją transferu regulatora PID

{\ Displaystyle C (s) = \ lewo (K_ {P} + K_ {I} \, {\ Frac {1} {s}} + K_ {D} \, s \ prawej).}

Jako przykład strojenia regulatora PID w układzie pętli zamkniętej $H (s)$ rozważmy instalację pierwszego rzędu określoną przez

{\ Displaystyle P (s) = {\ Frac {A} {1 + sT_ {P}}}}

gdzie $A$ i $T P$ są pewnymi stałymi. Wydajność instalacji jest przesyłana z powrotem

{\ Displaystyle F (s) = {\ Frac {1} {1 + sT_ {F}}}}

gdzie $T F$ jest również stałą. ${\ Displaystyle K_ {P} = K \ lewo (1 + {\ Frac {T_ {D}} {T_ {I}}} \ prawej)$ K. K $funkcję re = KT re$ i $szeregowej$ PID w

{\ Displaystyle C (s) = K \ lewo (1 + {\ Frac {1} {sT_ {I}}} \ prawo )(1+sT_{D})}

Podłączając $P (s)$ , $F (s)$ i $C (s) do funkcji przenoszenia$ $H (s)$ w zamkniętej pętli , stwierdzamy, że ustawiając

{\ Displaystyle K = {\ Frac {1} {A}}, T_ {I} = T_ {F}, T_ {D} = T_ {P }}

$H. (s) = 1$ . Przy takim dostrojeniu w tym przykładzie, wyjście systemowe jest dokładnie zgodne z wejściem referencyjnym.

Jednak w praktyce czysty wyróżnik nie jest fizycznie możliwy do zrealizowania ani pożądany ze względu na wzmocnienie szumu i modów rezonansowych w systemie. Dlatego kompensatora wyprzedzenia fazowego lub różnicownika z dolnoprzepustowym podbiciem.

Liniowa i nieliniowa teoria sterowania

Dziedzinę teorii sterowania można podzielić na dwie gałęzie:

Teoria sterowania liniowego – Dotyczy to systemów zbudowanych z urządzeń, które przestrzegają zasady superpozycji , co oznacza z grubsza, że wyjście jest proporcjonalne do wejścia. Rządzą nimi liniowe równania różniczkowe . Główną podklasą są systemy, które dodatkowo mają parametry niezmienne w czasie, zwane liniowymi niezmiennymi w czasie (LTI). Systemy te są podatne na potężne w dziedzinie częstotliwości o dużej ogólności, takie jak transformata Laplace'a , transformata Fouriera , transformata Z , wykres Bodego , locus root i kryterium stabilności Nyquista . Prowadzą one do opisu systemu przy użyciu terminów takich jak szerokość pasma , odpowiedź częstotliwościowa , wartości własne , wzmocnienie , częstotliwości rezonansowe , zera i bieguny , co daje rozwiązania dotyczące odpowiedzi systemu i technik projektowania dla większości interesujących systemów.
Teoria sterowania nieliniowego - obejmuje szerszą klasę systemów, które nie przestrzegają zasady superpozycji i ma zastosowanie do bardziej rzeczywistych systemów, ponieważ wszystkie rzeczywiste systemy sterowania są nieliniowe. Układy te są często zarządzane przez nieliniowe równania różniczkowe . Kilka technik matematycznych, które zostały opracowane do ich obsługi, jest trudniejszych i znacznie mniej ogólnych, często mających zastosowanie tylko do wąskich kategorii systemów. Obejmują one cykli granicznych , mapy Poincarégo , twierdzenie o stabilności Lapunowa i funkcje opisujące . Układy nieliniowe są często analizowane metodami numerycznymi na komputerach, na przykład symulując ich działanie za pomocą języka symulacyjnego . Jeśli interesujące są tylko rozwiązania w pobliżu stabilnego punktu, układy nieliniowe często można zlinearyzować , aproksymując je układem liniowym przy użyciu teorii zaburzeń i można zastosować techniki liniowe.

Techniki analizy - dziedzina częstotliwości i dziedzina czasu

Matematyczne techniki analizy i projektowania systemów sterowania dzielą się na dwie różne kategorie:

Dziedzina częstotliwości – w tym typie wartości zmiennych stanu , zmienne matematyczne reprezentujące wejście, wyjście i sprzężenie zwrotne systemu, są reprezentowane jako funkcje częstotliwości . Sygnał wejściowy i funkcja przenoszenia systemu są przekształcane z funkcji czasu na funkcje częstotliwości za pomocą transformacji , takiej jak transformata Fouriera , transformata Laplace'a lub transformacja Z. Zaletą tej techniki jest to, że powoduje uproszczenie matematyki; równania różniczkowe reprezentujące układ są zastępowane równaniami algebraicznymi w dziedzinie częstotliwości, które są znacznie prostsze do rozwiązania. Jednak techniki w dziedzinie częstotliwości mogą być stosowane tylko w systemach liniowych, jak wspomniano powyżej.
Reprezentacja w przestrzeni stanu w dziedzinie czasu - w tym typie wartości zmiennych stanu są reprezentowane jako funkcje czasu. W tym modelu analizowany system jest reprezentowany przez jedno lub więcej równań różniczkowych . Ponieważ techniki w dziedzinie częstotliwości są ograniczone do liniowych , dziedzina czasu jest szeroko stosowana do analizy systemów nieliniowych w świecie rzeczywistym. Chociaż są one trudniejsze do rozwiązania, nowoczesne techniki symulacji komputerowych, takie jak języki symulacyjne, uczyniły ich analizę rutynową.

W przeciwieństwie do analizy w dziedzinie częstotliwości klasycznej teorii sterowania, nowoczesna teoria sterowania wykorzystuje reprezentację w przestrzeni stanu w dziedzinie czasu , ^{[ potrzebne źródło ]} matematyczny model systemu fizycznego jako zestawu zmiennych wejściowych, wyjściowych i stanu powiązanych przez pierwsze- uporządkować równania różniczkowe. Abstrahując od liczby wejść, wyjść i stanów, zmienne są wyrażone jako wektory, a równania różniczkowe i algebraiczne są zapisywane w postaci macierzy (to ostatnie jest możliwe tylko wtedy, gdy układ dynamiczny jest liniowy). Reprezentacja w przestrzeni stanów (znana również jako „podejście w dziedzinie czasu”) zapewnia wygodny i kompaktowy sposób modelowania i analizowania systemów z wieloma wejściami i wyjściami. W przypadku wejść i wyjść musielibyśmy w przeciwnym razie zapisać transformaty Laplace'a, aby zakodować wszystkie informacje o systemie. W przeciwieństwie do podejścia opartego na dziedzinie częstotliwości, użycie reprezentacji w przestrzeni stanów nie ogranicza się do systemów o składowych liniowych i zerowych warunkach początkowych. „Przestrzeń stanu” odnosi się do przestrzeni, której osiami są zmienne stanu. Stan systemu można przedstawić jako punkt w tej przestrzeni.

Interfejsy systemowe - SISO i MIMO

Systemy sterowania można podzielić na różne kategorie w zależności od liczby wejść i wyjść.

Single-input single-output (SISO) – Jest to najprostszy i najczęściej spotykany typ, w którym jednym wyjściem steruje się jednym sygnałem sterującym. Przykładami są powyższy przykład tempomatu lub system audio , w którym wejściem sterującym jest wejściowy sygnał audio, a wyjściem są fale dźwiękowe z głośnika.
Multiple-input multiple-output (MIMO) – można je znaleźć w bardziej skomplikowanych systemach. Na przykład nowoczesne duże teleskopy , takie jak Keck i MMT , mają zwierciadła złożone z wielu oddzielnych segmentów, z których każdy jest kontrolowany przez siłownik . Kształt całego zwierciadła jest stale dostosowywany przez aktywny system sterowania optyką MIMO, wykorzystujący dane wejściowe z wielu czujników na płaszczyźnie ogniskowej, aby skompensować zmiany kształtu zwierciadła spowodowane rozszerzalnością cieplną, kurczeniem się, naprężeniami podczas obracania i zniekształceniem zwierciadła. czoła fali z powodu turbulencji w atmosferze. Skomplikowane systemy, takie jak reaktory jądrowe i ludzkie komórki , są symulowane przez komputer jako duże systemy sterowania MIMO.

Tematy z teorii sterowania

Stabilność

Stabilność ogólnego układu dynamicznego bez danych wejściowych można opisać za pomocą kryteriów stabilności Lapunowa .

System liniowy nazywany jest stabilnym z ograniczonym wejściem i ograniczonym wyjściem (BIBO), jeśli jego wyjście pozostanie ograniczone dla dowolnego ograniczonego wejścia.
Stabilność dla systemów nieliniowych , które pobierają dane wejściowe, to stabilność wejścia do stanu (ISS), która łączy stabilność Lapunowa i pojęcie podobne do stabilności BIBO.

systemach liniowych w czasie ciągłym i dyskretnym .

Z matematycznego punktu widzenia oznacza to, że aby liniowy układ przyczynowy był stabilny, wszystkie bieguny jego funkcji przejścia muszą mieć wartości ujemne, tj. część rzeczywista każdego bieguna musi być mniejsza od zera. Praktycznie rzecz biorąc, stabilność wymaga, aby rezydowały złożone bieguny funkcji przenoszenia

w otwartej lewej połowie płaszczyzny zespolonej przez czas ciągły, gdy transformata Laplace'a jest używana do uzyskania funkcji przenoszenia.
wewnątrz okręgu jednostkowego przez czas dyskretny, gdy stosowana jest transformacja Z.

Różnica między tymi dwoma przypadkami wynika po prostu z tradycyjnej metody wykreślania funkcji transferu czasu ciągłego i dyskretnego. Ciągła transformata Laplace'a jest we współrzędnych kartezjańskich , gdzie $,$ jest osią rzeczywistą, a dyskretna transformata Z jest we $współrzędnych$ kołowych gdzie jest osią rzeczywistą.

Gdy spełnione są powyższe warunki, mówi się, że system jest asymptotycznie stabilny ; zmienne asymptotycznie stabilnego układu sterowania zawsze maleją od wartości początkowej i nie wykazują trwałych oscylacji. Oscylacje trwałe występują, gdy biegun ma część rzeczywistą dokładnie równą zeru (w przypadku czasu ciągłego) lub moduł równy jeden (w przypadku czasu dyskretnego). Jeśli po prostu stabilna odpowiedź systemu ani nie zanika, ani nie rośnie w czasie i nie ma oscylacji, jest marginalnie stabilna ; w tym przypadku funkcja przenoszenia systemu ma niepowtarzające się bieguny na początku płaszczyzny zespolonej (tj. ich składowa rzeczywista i zespolona wynosi zero w przypadku czasu ciągłego). Oscylacje występują, gdy bieguny o części rzeczywistej równej zeru mają część urojoną różną od zera.

Jeśli dany system ma odpowiedź impulsową

{\ Displaystyle \ x [n] = 0,5 ^ {n} u [n]}

wtedy transformacja Z (patrz ten przykład ) jest dana przez

{\ Displaystyle \ X (z) = {\ Frac {1} {1-0,5 z ^ {- 1}}}}

który ma biegun $($ zero części urojonej Ten system jest BIBO (asymptotycznie) stabilny, ponieważ biegun znajduje się wewnątrz okręgu jednostkowego.

Jeśli jednak odpowiedź impulsowa była

{\ Displaystyle \ x [n] = 1,5 ^ {n} u [n]}

wtedy jest transformacja Z

{\ Displaystyle \ X (z) = {\ Frac {1} {1-1,5 z ^ {- 1}}}}

który ma biegun w punkcie $BIBO,$ moduł ściśle większy niż jeden.

Istnieje wiele narzędzi do analizy biegunów systemu. Obejmują one systemy graficzne, takie jak locus korzenia , wykresy Bodego lub wykresy Nyquista .

Zmiany mechaniczne mogą sprawić, że sprzęt (i systemy sterowania) będą bardziej stabilne. Marynarze dodają balast, aby poprawić stateczność statków. Statki wycieczkowe używają płetw przeciwprzechylnych , które rozciągają się poprzecznie od burty statku na około 30 stóp (10 m) i są stale obracane wokół swoich osi, aby wytworzyć siły przeciwdziałające przechyłowi.

Kontrolowalność i obserwowalność

Kontrolowalność i obserwowalność to główne kwestie w analizie systemu przed podjęciem decyzji o zastosowaniu najlepszej strategii sterowania lub o tym, czy w ogóle możliwe jest kontrolowanie lub stabilizowanie systemu. Sterowalność związana jest z możliwością wymuszenia na systemie określonego stanu za pomocą odpowiedniego sygnału sterującego. Jeśli stan nie jest kontrolowany, żaden sygnał nigdy nie będzie w stanie kontrolować tego stanu. Jeśli stan nie jest sterowalny, ale jego dynamika jest stabilna, wówczas stan ten jest określany jako stabilizowany . Obserwowalność jest natomiast związana z możliwością obserwowania , poprzez pomiary wyjściowe, stanu systemu. Jeśli stan nie jest obserwowalny, kontroler nigdy nie będzie w stanie określić zachowania stanu nieobserwowalnego, a zatem nie może go użyć do ustabilizowania systemu. Jednak, podobnie jak w przypadku warunku stabilności powyżej, jeśli nie można zaobserwować stanu, może on nadal być wykrywalny.

Z geometrycznego punktu widzenia, patrząc na stany każdej zmiennej systemu, który ma być kontrolowany, każdy „zły” stan tych zmiennych musi być kontrolowany i obserwowalny, aby zapewnić dobre zachowanie w systemie z zamkniętą pętlą. Oznacza to, że jeśli jedna z wartości własnych systemu nie jest zarówno kontrolowana, jak i obserwowalna, ta część dynamiki pozostanie nietknięta w systemie z zamkniętą pętlą. Jeśli taka wartość własna nie jest stabilna, dynamika tej wartości własnej będzie obecna w układzie zamkniętym, który w związku z tym będzie niestabilny. Nieobserwowalne bieguny nie występują w realizacji funkcji przenoszenia reprezentacji w przestrzeni stanów, dlatego czasami ta ostatnia jest preferowana w analizie systemów dynamicznych.

Rozwiązania problemów niekontrolowanego lub nieobserwowalnego systemu obejmują dodanie siłowników i czujników.

Specyfikacja sterowania

W ostatnich latach opracowano kilka różnych strategii kontroli. Różnią się one od bardzo ogólnych (regulator PID), do innych poświęconych bardzo szczególnym klasom systemów (zwłaszcza robotyce czy tempomatowi samolotu).

Problem ze sterowaniem może mieć kilka specyfikacji. Stabilność jest oczywiście zawsze obecna. Sterownik musi zapewnić, że system w pętli zamkniętej jest stabilny, niezależnie od stabilności w pętli otwartej. Zły wybór kontrolera może nawet pogorszyć stabilność systemu z otwartą pętlą, czego zwykle należy unikać. Czasami pożądane byłoby uzyskanie określonej dynamiki w pętli zamkniętej: tj. Bieguny mają $[\ lambda ] <- {\ overline {\ lambda}}}$ Re ${\ Displaystyle {\ overline {\ lambda}}}$ jest stałą wartością ściśle większą od zera, zamiast po prostu o to pytać ${\ Displaystyle Re [\ lambda] <0}$ .

Inną typową specyfikacją jest odrzucenie zakłócenia krokowego; włączenie integratora w łańcuch otwartej pętli (tj. bezpośrednio przed kontrolowanym systemem) pozwala to łatwo osiągnąć. Inne klasy zakłóceń wymagają uwzględnienia różnych typów podsystemów.

Inne „klasyczne” specyfikacje teorii sterowania dotyczą odpowiedzi czasowej systemu z zamkniętą pętlą. Należą do nich czas narastania (czas potrzebny układowi sterowania do osiągnięcia żądanej wartości po zaburzeniu), przeregulowanie szczytowe (najwyższa wartość osiągnięta przez odpowiedź przed osiągnięciem żądanej wartości) i inne ( czas ustalania , ćwiartka zaniku). Specyfikacje w dziedzinie częstotliwości są zwykle związane z odpornością (patrz dalej).

Nowoczesne oceny wydajności wykorzystują pewną odmianę zintegrowanego błędu śledzenia (IAE, ISA, CQI).

Identyfikacja modelu i solidność

System sterowania zawsze musi mieć pewną właściwość odporności. Solidny kontroler to taki, że jego właściwości nie zmieniają się zbytnio, jeśli zastosuje się go do systemu nieco różniącego się od matematycznego używanego do jego syntezy. To wymaganie jest ważne, ponieważ żaden rzeczywisty układ fizyczny nie zachowuje się tak, jak seria równań różniczkowych użytych do jego matematycznego przedstawienia. Zwykle wybiera się prostszy model matematyczny w celu uproszczenia obliczeń, w przeciwnym razie prawdziwa dynamika systemu może być tak skomplikowana, że kompletny model jest niemożliwy.

Identyfikacja systemu

Proces wyznaczania równań rządzących dynamiką modelu nazywa się identyfikacją systemu . Można to zrobić w trybie offline: na przykład wykonując serię miar, na podstawie których można obliczyć przybliżony model matematyczny, zazwyczaj jego funkcję przenoszenia lub macierz. Taka identyfikacja z danych wyjściowych nie może jednak uwzględniać nieobserwowalnej dynamiki. Czasami model jest budowany bezpośrednio ze znanych równań fizycznych, np. w przypadku masa-sprężyna-tłumik wiemy, że ${ \ Displaystyle m {\ ddot {x}} (t) = - Kx (t) - \ operatorname {B} {\ kropka {x}} (t)}$ . Nawet zakładając, że do projektowania regulatora używany jest „kompletny” model, wszystkie parametry zawarte w tych równaniach (zwane „parametrami nominalnymi”) nigdy nie są znane z absolutną precyzją; system sterowania będzie musiał zachowywać się poprawnie nawet po podłączeniu do systemu fizycznego z rzeczywistymi wartościami parametrów odbiegającymi od nominalnych.

Niektóre zaawansowane techniki kontroli obejmują proces identyfikacji „on-line” (patrz dalej). Parametry modelu są obliczane („identyfikowane”) podczas pracy samego sterownika. W ten sposób, jeśli nastąpi drastyczna zmiana parametrów, na przykład, jeśli ramię robota zwolni ciężarek, kontroler konsekwentnie dostosuje się, aby zapewnić prawidłowe działanie.

Analiza

Analizę odporności systemu sterowania SISO (jedno wejście, jedno wyjście) można przeprowadzić w dziedzinie częstotliwości, biorąc pod uwagę funkcję przenoszenia systemu i używając diagramów Nyquista i Bodego . Tematy obejmują margines wzmocnienia i fazy oraz margines amplitudy. W przypadku MIMO (multi-input multi-output) i ogólnie bardziej skomplikowanych systemów sterowania, należy wziąć pod uwagę teoretyczne wyniki opracowane dla każdej techniki sterowania (patrz następna sekcja). To znaczy, jeśli potrzebne są szczególne cechy solidności, inżynier musi skierować swoją uwagę na technikę sterowania, włączając te cechy do jej właściwości.

Ograniczenia

Szczególnym problemem związanym z odpornością jest wymaganie, aby system sterowania działał prawidłowo w obecności ograniczeń wejściowych i stanu. W świecie fizycznym każdy sygnał jest ograniczony. Może się zdarzyć, że sterownik będzie wysyłał sygnały sterujące, których system fizyczny nie może nadążyć, na przykład próbując obrócić zawór z nadmierną prędkością. Może to spowodować niepożądane zachowanie systemu w pętli zamkniętej, a nawet uszkodzenie lub uszkodzenie siłowników lub innych podsystemów. Aby rozwiązać ten problem, dostępne są określone techniki sterowania: modelowe sterowanie predykcyjne (patrz dalej) i systemy zapobiegające nawijaniu . Ten ostatni składa się z dodatkowego bloku sterującego, który zapewnia, że sygnał sterujący nigdy nie przekroczy zadanego progu.

Klasyfikacje systemowe

Sterowanie układami liniowymi

W przypadku systemów MIMO rozmieszczenie biegunów można przeprowadzić matematycznie, stosując reprezentację w przestrzeni stanów systemu z otwartą pętlą i obliczając macierz sprzężenia zwrotnego, przypisując bieguny w żądanych pozycjach. W skomplikowanych systemach może to wymagać możliwości obliczeń wspomaganych komputerowo i nie zawsze może zapewnić solidność. Co więcej, wszystkie stany systemu nie są generalnie mierzone, dlatego też obserwatorzy muszą być uwzględnieni i włączeni do projektu rozmieszczenia biegunów.

Sterowanie układami nieliniowymi

Procesy w branżach takich jak robotyka i przemysł lotniczy mają zazwyczaj silną nieliniową dynamikę. W teorii sterowania czasami możliwa jest linearyzacja takich klas systemów i zastosowanie technik liniowych, ale w wielu przypadkach konieczne może być opracowanie od podstaw teorii pozwalających na sterowanie układami nieliniowymi. Te, np. linearyzacja ze sprzężeniem zwrotnym , krok wstecz , sterowanie trybem ślizgowym , sterowanie linearyzacją trajektorii zwykle wykorzystują wyniki oparte na teorii Lapunowa . Geometria różniczkowa była szeroko stosowana jako narzędzie do uogólniania dobrze znanych koncepcji sterowania liniowego na przypadek nieliniowy, a także do pokazywania subtelności, które czynią ten problem trudniejszym. Teoria kontroli została również wykorzystana do rozszyfrowania mechanizmu neuronowego, który kieruje stanami poznawczymi.

Sterowanie systemami zdecentralizowanymi

Gdy system jest kontrolowany przez wiele sterowników, problemem jest zdecentralizowana kontrola. Decentralizacja jest pomocna na wiele sposobów, na przykład pomaga systemom kontroli działać na większym obszarze geograficznym. Agenci w zdecentralizowanych systemach kontroli mogą wchodzić w interakcje za pomocą kanałów komunikacyjnych i koordynować swoje działania.

Sterowanie układami deterministycznymi i stochastycznymi

Stochastyczny problem sterowania to taki, w którym ewolucja zmiennych stanu jest poddawana losowym szokom spoza systemu. Deterministyczny problem sterowania nie podlega zewnętrznym przypadkowym szokom.

Główne strategie sterowania

Każdy system sterowania musi przede wszystkim gwarantować stabilność działania w pętli zamkniętej. W przypadku systemów liniowych można to uzyskać przez bezpośrednie umieszczenie biegunów. Nieliniowe systemy sterowania wykorzystują określone teorie (zwykle oparte na Aleksandra Lapunowa ), aby zapewnić stabilność bez względu na wewnętrzną dynamikę systemu. Możliwość spełnienia różnych specyfikacji różni się w zależności od rozważanego modelu i wybranej strategii kontroli.

Lista głównych technik kontroli

Sterowanie adaptacyjne wykorzystuje identyfikację on-line parametrów procesu lub modyfikację wzmocnień regulatora, uzyskując w ten sposób silne właściwości wytrzymałościowe. Sterowanie adaptacyjne zostało po raz pierwszy zastosowane w przemyśle lotniczym w latach pięćdziesiątych XX wieku i odniosło szczególny sukces w tej dziedzinie.
Hierarchiczny system sterowania to rodzaj systemu sterowania , w którym zestaw urządzeń i oprogramowania sterującego jest ułożony w hierarchiczne drzewo . Gdy powiązania w drzewie realizowane są przez sieć komputerową , to ten hierarchiczny system sterowania jest również formą sieciowego systemu sterowania .
Inteligentne sterowanie wykorzystuje różne podejścia obliczeniowe AI, takie jak sztuczne sieci neuronowe , prawdopodobieństwo bayesowskie , logika rozmyta , uczenie maszynowe , obliczenia ewolucyjne i algorytmy genetyczne lub kombinację tych metod, takich jak algorytmy neurorozmyte , do sterowania systemem dynamicznym .
Sterowanie optymalne to szczególna technika sterowania, w której sygnał sterujący optymalizuje pewien „wskaźnik kosztów”: na przykład w przypadku satelity pchnięcia odrzutowca potrzebne do doprowadzenia go do pożądanej trajektorii, która zużywa najmniej paliwa. Dwie optymalne metody projektowania sterowania są szeroko stosowane w zastosowaniach przemysłowych, ponieważ wykazano, że mogą one zagwarantować stabilność pętli zamkniętej. Są to sterowanie predykcyjne modelu (MPC) i sterowanie liniowo-kwadratowo-gaussowskie (LQG). Pierwsza może bardziej jednoznacznie uwzględniać ograniczenia sygnałów w systemie, co jest ważną cechą w wielu procesach przemysłowych. Jednak struktura „optymalnego sterowania” w MPC jest tylko środkiem do osiągnięcia takiego rezultatu, ponieważ nie optymalizuje rzeczywistego wskaźnika wydajności układu sterowania w pętli zamkniętej. Wraz z regulatorami PID systemy MPC są najczęściej stosowaną techniką sterowania w sterowaniu procesami .
Solidne sterowanie wyraźnie zajmuje się niepewnością w swoim podejściu do projektowania kontrolera. Sterowniki zaprojektowane przy użyciu niezawodnych metod sterowania są zwykle w stanie poradzić sobie z niewielkimi różnicami między rzeczywistym systemem a nominalnym modelem używanym do projektowania. Wczesne metody Bodego i innych były dość solidne; czasami okazywało się, że metody przestrzeni stanów wynalezione w latach sześćdziesiątych i siedemdziesiątych nie są solidne. Przykłady nowoczesnych niezawodnych technik sterowania obejmują kształtowanie pętli H-nieskończoności opracowane przez Duncana McFarlane'a i Keitha Glovera , sterowanie trybem ślizgowym (SMC) opracowane przez Vadima Utkina oraz bezpieczne protokoły zaprojektowane do sterowania dużymi heterogenicznymi populacjami obciążeń elektrycznych w aplikacjach Smart Power Grid . Solidne metody mają na celu osiągnięcie solidnej wydajności i/lub stabilności w obecności małych błędów modelowania.
Sterowanie stochastyczne zajmuje się projektowaniem sterowania z niepewnością w modelu. W typowych problemach sterowania stochastycznego zakłada się, że w modelu i regulatorze występują losowe szumy i zakłócenia, a projekt sterowania musi uwzględniać te przypadkowe odchylenia.
Samoorganizującą się kontrolę krytyczności można zdefiniować jako próby ingerencji w procesy, za pomocą których samoorganizujący się system rozprasza energię.

Ludzie w systemach i kontroli

Wiele aktywnych i historycznych postaci wniosło znaczący wkład w teorię sterowania, w tym

Pierre-Simon Laplace wynalazł transformację Z w swojej pracy nad teorią prawdopodobieństwa , obecnie używaną do rozwiązywania problemów teorii sterowania w czasie dyskretnym. Transformata Z jest odpowiednikiem w czasie dyskretnym transformaty Laplace'a , która została nazwana jego imieniem.
Irmgard Flugge-Lotz opracowała teorię nieciągłego automatycznego sterowania i zastosowała ją do automatycznych systemów sterowania samolotami .
Aleksander Lapunow w latach 90. XIX wieku wyznacza początek teorii stabilności .
Harold S. Black wynalazł koncepcję wzmacniaczy z ujemnym sprzężeniem zwrotnym w 1927 roku. Udało mu się opracować stabilne wzmacniacze z ujemnym sprzężeniem zwrotnym w latach trzydziestych XX wieku.
Harry Nyquist opracował kryterium stabilności Nyquista dla systemów sprzężenia zwrotnego w latach trzydziestych XX wieku.
Richard Bellman opracował programowanie dynamiczne w latach czterdziestych XX wieku.
Warren E. Dixon , teoretyk sterowania i profesor
Andrey Kolmogorov współtworzył filtr Wienera-Kołmogorowa w 1941 roku.
Norbert Wiener był współtwórcą filtra Wienera-Kołmogorowa i ukuł termin cybernetyka w latach czterdziestych XX wieku.
John R. Ragazzini wprowadził sterowanie cyfrowe i zastosowanie transformacji Z w teorii sterowania (wynalezionej przez Laplace'a) w latach pięćdziesiątych XX wieku.
Lew Pontryagin przedstawił zasadę maksimum i zasadę bang-bang .
Pierre-Louis Lions opracował rozwiązania dotyczące lepkości w zakresie kontroli stochastycznej i optymalnych metod kontroli.
Rudolf E. Kálmán był pionierem podejścia do systemów i kontroli w przestrzeni stanów . Wprowadził pojęcia sterowalności i obserwowalności . Opracował filtr Kalmana do estymacji liniowej.
Ali H. Nayfeh , który był jednym z głównych współtwórców nieliniowej teorii sterowania i opublikował wiele książek o metodach perturbacji
Jan C. Willems wprowadził pojęcie dyssypatywności jako uogólnienie funkcji Lapunowa na systemy wejścia/stanu/wyjścia. Konstrukcja funkcji przechowywania, jak nazywa się analog funkcji Lapunowa, doprowadziła do badania liniowej nierówności macierzy (LMI) w teorii sterowania. Był pionierem behawioralnego podejścia do matematycznej teorii systemów.

Zobacz też

Przykłady systemów sterowania

Tematy z teorii sterowania

Inne powiązane tematy

Dalsza lektura

Levine, William S., wyd. (1996). Podręcznik sterowania . Nowy Jork: CRC Press. ISBN 978-0-8493-8570-4 .
Karla J. Åströma; Richarda M. Murraya (2008). Systemy sprzężenia zwrotnego: wprowadzenie dla naukowców i inżynierów (PDF) . Wydawnictwo Uniwersytetu Princeton. ISBN 978-0-691-13576-2 .
Krzysztof Kilian (2005). Nowoczesna technologia sterowania . Nauka Thompsona Delmara. ISBN 978-1-4018-5806-3 .
Vannevara Busha (1929). Analiza obwodu operacyjnego . John Wiley and Sons, Inc.
Robert F. Stengel (1994). Optymalna kontrola i szacowanie . Publikacje Dover. ISBN 978-0-486-68200-6 .
Franklina; i in. (2002). Kontrola sprzężenia zwrotnego systemów dynamicznych (4 wyd.). New Jersey: Prentice Hall. ISBN 978-0-13-032393-4 .
Joseph L. Hellerstein; Świt M. Tilbury ; Sujay Parekh (2004). Kontrola sprzężenia zwrotnego systemów komputerowych . John Wiley i synowie. ISBN 978-0-471-26637-2 .
Diederich Hinrichsen i Anthony J. Pritchard (2005). Teoria systemów matematycznych I - modelowanie, analiza przestrzeni stanów, stabilność i odporność . Skoczek. ISBN 978-3-540-44125-0 .
Andrei, Neculai (2005). „Nowoczesna teoria sterowania - perspektywa historyczna” (PDF) . Źródło 10 października 2007 . {{ cite journal }} : Cite journal wymaga |journal= ( pomoc )
Sontag Eduardo (1998). Matematyczna teoria sterowania: deterministyczne skończone systemy wymiarowe . Wydanie drugie (PDF) . Skoczek. ISBN 978-0-387-98489-6 .
Goodwin, Graham (2001). Projekt systemu sterowania . Sala Prentice'a. ISBN 978-0-13-958653-8 .
Christophe Basso (2012). Projektowanie pętli sterowania dla zasilaczy liniowych i impulsowych: przewodnik samouczek . Dom Artecha. ISBN 978-1608075577 .
Boris J. Lurie; Paul J. Enright (2019). Klasyczna kontrola sprzężenia zwrotnego z nieliniowymi systemami wielopętlowymi (wyd. 3). Prasa CRC. ISBN 978-1-1385-4114-6 .

Dla inżynierii chemicznej

Luyben, William (1989). Modelowanie procesów, symulacje i sterowanie dla inżynierów chemików . Wzgórze McGrawa. ISBN 978-0-07-039159-8 .

Linki zewnętrzne

Samouczki sterowania dla Matlaba , zestaw sprawdzonych przykładów sterowania rozwiązanych kilkoma różnymi metodami.
Strojenie sterowania i najlepsze praktyki
Zaawansowane struktury sterowania, bezpłatne symulatory on-line wyjaśniające teorię sterowania

Teoria sterowania
Gałęzie	Sterowanie adaptacyjne Teoria sterowania Sterowanie cyfrowe Kontrola kształtowania energii Rozmyta kontrola Sterowanie hybrydowe Inteligentna kontrola Sterowanie predykcyjne modelu Sterowanie wielowymiarowe Kontrola neuronowa Sterowanie nieliniowe Optymalna kontrola Kontrola w czasie rzeczywistym Solidna kontrola Kontrola stochastyczna
Właściwości systemu	Fabuła Bodego Schemat blokowy Funkcja przesyłania w pętli zamkniętej Kontrolowalność Transformata Fouriera Pasmo przenoszenia Transformata Laplace'a Negatywne opinie Obserwowalność Wydajność Pozytywne opinie Metoda Locus Root Serwomechanizm Wykres przepływu sygnału Reprezentacja w przestrzeni stanów Teoria stabilności Analiza i projektowanie w stanie ustalonym Dynamika systemu Funkcja transferu
Sterowanie cyfrowe	Sygnał w czasie dyskretnym Przetwarzanie sygnału cyfrowego Kwantyzacja Oprogramowanie czasu rzeczywistego Próbkowane dane Identyfikacja systemu Transformacja Z
Zaawansowane techniki	Sztuczna sieć neuronowa Metoda wykresów współczynników Rekonfiguracja sterowania Rozproszone systemy parametrów Kontrola rzędu ułamkowego Logika rozmyta Kształtowanie pętli w nieskończoność H Wartość osobliwa Hankla Filtr Kalmana Twierdzenie Krenera Najmniejsze kwadraty Stabilność Lapunowa Niewielkie sprzężenie zwrotne pętli Teoria kontroli percepcyjnej Obserwator stanu Sterowanie wektorowe
Kontrolery	Wbudowany kontroler Sterownik w pętli zamkniętej Kompensator opóźnienia wyprzedzania Kontrola numeryczna regulator PID Programowalny sterownik logiczny
Aplikacje kontrolne	Automatyka i zdalne sterowanie Rozproszony system sterowania Silniki elektryczne Przemysłowe systemy sterowania Mechatronika Kontrola ruchu Kontrola procesu Robotyka Kontrola nadzorcza (SCADA)

Matematyka
Oś czasu historii Zarys Listy Słowniczek
Podwaliny	Teoria kategorii Teoria informacji Logika matematyczna Filozofia matematyki Teoria mnogości Teoria typów
Algebra	Abstrakcyjny przemienny Podstawowy Teoria grup Liniowy Wieloliniowy uniwersalny Homologiczny
Analiza	Rachunek różniczkowy Prawdziwa analiza Złożona analiza Analiza hiperzłożona Równania różniczkowe Analiza funkcjonalna Analiza harmoniczna Teoria miary
Oddzielny	Kombinatoryka Teoria grafów Teoria porządku
Geometria	Algebraiczny Analityczny Arytmetyka Mechanizm różnicowy Oddzielny euklidesowy Skończone
Teoria liczb	Arytmetyka Algebraiczna teoria liczb Analityczna teoria liczb Geometria diofantyczna
Topologia	Ogólny Algebraiczny Mechanizm różnicowy Geometryczny Teoria homotopii
Stosowany	Matematyka inżynierska Biologia matematyczna Chemia matematyczna Ekonomia matematyczna Finanse matematyczne Fizyka matematyczna Psychologia matematyczna Socjologia matematyczna Statystyka matematyczna Prawdopodobieństwo Statystyka Nauka o systemach Teoria sterowania Teoria gry Badania operacyjne
Obliczeniowy	Informatyka Teoria obliczeń Teoria złożoności obliczeniowej Analiza numeryczna Optymalizacja Algebra komputerowa
powiązane tematy	Matematyka nieformalna Matematyka rekreacyjna Matematyka i sztuka Edukacja matematyczna
Portal matematyczny Kategoria Lud WikiProjekt