Rachunek różniczkowy
| Część serii artykułów o |
| rachunku różniczkowym |
|---|
| Matematyka | ||
|---|---|---|
|
|
||
| Portal | ||
Rachunek różniczkowy , pierwotnie nazywany rachunkiem nieskończenie małym lub „rachunkiem nieskończenie małych ”, jest matematycznym badaniem ciągłych zmian, w taki sam sposób, w jaki geometria jest badaniem kształtu, a algebra jest badaniem uogólnień operacji arytmetycznych .
Ma dwie główne gałęzie, rachunek różniczkowy i rachunek całkowy ; pierwsza dotyczy chwilowych szybkości zmian i nachyleń krzywych , podczas gdy druga dotyczy akumulacji wielkości i obszarów pod lub pomiędzy krzywymi. Te dwie gałęzie są powiązane ze sobą fundamentalnym twierdzeniem rachunku różniczkowego i wykorzystują podstawowe pojęcia zbieżności nieskończonych ciągów i nieskończonych szeregów do dobrze określonej granicy .
Rachunek nieskończenie mały został opracowany niezależnie pod koniec XVII wieku przez Izaaka Newtona i Gottfrieda Wilhelma Leibniza . Późniejsze prace, w tym kodyfikowanie idei granic , postawiły te zmiany na bardziej solidnych podstawach koncepcyjnych. Obecnie rachunek różniczkowy ma szerokie zastosowanie w nauce , inżynierii i naukach społecznych .
Etymologia
W edukacji matematycznej rachunek różniczkowy oznacza kursy elementarnej analizy matematycznej , które są głównie poświęcone badaniu funkcji i granic. Słowo rachunek różniczkowy to po łacinie „mały kamyk” ( zdrobnienie od calx istnieje oznaczające „kamień”), znaczenie, które nadal w medycynie . Ponieważ takich kamyków używano do odliczania odległości, liczenia głosów i wykonywania liczydłem , słowo to zaczęło oznaczać metodę obliczeń. W tym sensie używano go w języku angielskim przynajmniej już w 1672 r., kilka lat przed publikacjami Leibniza i Newtona.
Oprócz rachunku różniczkowego i rachunku całkowego termin ten jest również używany do nazywania określonych metod obliczeniowych i powiązanych teorii, które mają na celu modelowanie określonej koncepcji w kategoriach matematycznych. Przykłady tej konwencji obejmują rachunek zdań , rachunek Ricciego , rachunek wariacyjny , rachunek lambda i rachunek procesów . Co więcej, termin „rachunek” był różnie stosowany w etyce i filozofii dla takich systemów, jak rachunek szczęścia Benthama i rachunek etyczny .
Historia
Współczesny rachunek różniczkowy został opracowany w XVII-wiecznej Europie przez Izaaka Newtona i Gottfrieda Wilhelma Leibniza (niezależnie od siebie, pierwsze publikacje w tym samym czasie), ale jego elementy pojawiły się w starożytnej Grecji, potem w Chinach i na Bliskim Wschodzie, a jeszcze później znowu w średniowiecznej Europie i Indiach.
Starożytni prekursorzy
Egipt
Obliczenia objętości i powierzchni , jeden z celów rachunku całkowego, można znaleźć w egipskim papirusie moskiewskim ( ok. 1820 pne), ale wzory są prostymi instrukcjami, bez wskazania, w jaki sposób zostały uzyskane.
Grecja
Kładąc podwaliny pod rachunek całkowy i zapowiadając koncepcję granicy, starożytny grecki matematyk Eudoksos z Knidos ( ok. 390 – 337 pne) opracował metodę wyczerpania , aby udowodnić wzory na objętości stożka i piramidy.
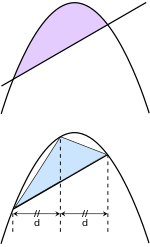
W okresie hellenistycznym metoda ta została rozwinięta przez Archimedesa ( ok. 287 – ok. 212 pne ), który połączył ją z koncepcją niepodzielnych — prekursorem liczb nieskończenie małych — co pozwoliło mu rozwiązać kilka problemów, którymi obecnie zajmuje się rachunek całkowy. W Metodzie twierdzeń mechanicznych opisuje. na przykład obliczanie środka ciężkości półkuli bryłowej , środka ciężkości ściętego paraboloidy kołowej oraz pola obszaru ograniczonego parabolą i jedną z jej siecznych linii .
Chiny
Metoda wyczerpania została później odkryta niezależnie w Chinach przez Liu Hui w III wieku naszej ery w celu znalezienia pola koła. W V wieku naszej ery Zu Gengzhi , syn Zu Chongzhi , ustalił metodę, która później została nazwana zasadą Cavalieriego , aby znaleźć objętość kuli .
Średniowieczny
Bliski Wschód
Na Bliskim Wschodzie Hasan Ibn al-Haytham , zlatynizowany jako Alhazen ( ok. 965 – ok. 1040 r.), wyprowadził wzór na sumę potęg czwartych . Wykorzystał wyniki do przeprowadzenia czegoś, co teraz nazwalibyśmy całkowaniem tej funkcji, gdzie wzory na sumy całkowitych kwadratów i potęg czwartych pozwoliły mu obliczyć objętość paraboloidy .
Indie
W XIV wieku matematycy indyjscy podali nieścisłą metodę, przypominającą różniczkowanie, stosowaną do niektórych funkcji trygonometrycznych. Madhava z Sangamagrama i Kerala School of Astronomy and Mathematics określili w ten sposób składniki rachunku różniczkowego. Kompletna teoria obejmująca te składowe jest obecnie dobrze znana w świecie zachodnim jako szereg Taylora lub przybliżenie szeregów nieskończonych . Jednak nie byli w stanie „połączyć wielu różnych pomysłów w ramach dwóch jednoczących tematów pochodnej i całki , pokazać związek między nimi i przekształcić rachunek różniczkowy w wspaniałe narzędzie do rozwiązywania problemów, które mamy dzisiaj”.
Nowoczesny
Praca Johannesa Keplera Stereometrica Doliorum stworzyła podstawę rachunku całkowego. Kepler opracował metodę obliczania powierzchni elipsy poprzez dodanie długości wielu promieni wykreślonych z ogniska elipsy.
Znaczącym dziełem był traktat, wywodzący się z metod Keplera, napisany przez Bonaventurę Cavalieri , który argumentował, że objętości i powierzchnie należy obliczać jako sumy objętości i powierzchni nieskończenie cienkich przekrojów. Pomysły były podobne do Archimedesa w The Method , ale uważa się, że traktat ten zaginął w XIII wieku i został ponownie odkryty dopiero na początku XX wieku, więc byłby nieznany Cavalieri. Praca Cavalieriego nie była dobrze szanowana, ponieważ jego metody mogły prowadzić do błędnych wyników, a nieskończenie małe ilości, które wprowadził, były początkowo haniebne.
Formalne badanie rachunku różniczkowego połączyło nieskończenie małe Cavalieriego z rachunkiem różnic skończonych , który rozwinął się w Europie mniej więcej w tym samym czasie. Pierre de Fermat , twierdząc, że zapożyczył od Diofantusa , wprowadził pojęcie adekwatności , które reprezentowało równość aż do nieskończenie małego składnika błędu. Połączenie zostało osiągnięte przez Johna Wallisa , Isaaca Barrowa i Jamesa Gregory'ego , dwóch ostatnich udowadniających poprzedników drugiego podstawowego twierdzenia rachunku różniczkowego około 1670 roku.
Reguła iloczynu i reguła łańcuchowa , pojęcia wyższych pochodnych i szeregu Taylora oraz funkcje analityczne były używane przez Isaaca Newtona w specyficznej notacji, którą stosował do rozwiązywania problemów fizyki matematycznej . W swoich pracach Newton przeformułował swoje idee, aby pasowały do idiomu matematycznego tamtych czasów, zastępując obliczenia nieskończenie małymi równoważnymi argumentami geometrycznymi, które uznano za bez zarzutu. Użył metod rachunku różniczkowego do rozwiązania problemu ruchu planet, kształtu powierzchni wirującego płynu, spłaszczenia Ziemi, ruchu ciężaru ślizgającego się po cykloidzie i wielu innych problemów omówionych w jego Principia Mathematica ( 1687). W innej pracy opracował rozwinięcia szeregów dla funkcji, w tym potęg ułamkowych i niewymiernych, i było jasne, że rozumie zasady szeregu Taylora . Nie opublikował wszystkich tych odkryć, aw tamtym czasie nieskończenie małe metody nadal uważano za niegodne.
Idee te zostały ułożone w prawdziwy rachunek nieskończenie małych przez Gottfrieda Wilhelma Leibniza , który został pierwotnie oskarżony o plagiat przez Newtona. Obecnie jest uważany za niezależnego wynalazcę i współtwórcę rachunku różniczkowego. Jego wkład polegał na zapewnieniu jasnego zestawu reguł pracy z nieskończenie małymi wielkościami, umożliwiającego obliczanie drugich i wyższych pochodnych oraz zapewnienie reguły iloczynu i reguły łańcuchowej w ich postaciach różniczkowych i całkowych. W przeciwieństwie do Newtona, Leibniz włożył żmudny wysiłek w wybór notacji.
Obecnie Leibnizowi i Newtonowi przypisuje się zwykle uznanie za niezależne wynalezienie i rozwój rachunku różniczkowego. Newton był pierwszym, który zastosował rachunek różniczkowy do fizyki ogólnej , a Leibniz rozwinął większość notacji używanej obecnie w rachunku różniczkowym. Podstawowymi spostrzeżeniami, których dostarczyli zarówno Newton, jak i Leibniz, były prawa różniczkowania i całkowania, podkreślając, że różniczkowanie i całkowanie to procesy odwrotne, drugie i wyższe pochodne oraz pojęcie przybliżonego szeregu wielomianowego.
Kiedy Newton i Leibniz po raz pierwszy opublikowali swoje wyniki, istniały wielkie kontrowersje co do tego, który matematyk (a zatem który kraj) zasługiwał na uznanie. Newton wyprowadził swoje wyniki jako pierwszy (później został opublikowany w jego Method of Fluxions ), ale Leibniz jako pierwszy opublikował swoją „ Nova Methodus pro Maximis et Minimis ”. Newton twierdził, że Leibniz ukradł pomysły z jego niepublikowanych notatek, którymi Newton podzielił się z kilkoma członkami Towarzystwa Królewskiego . Ta kontrowersja przez wiele lat dzieliła anglojęzycznych matematyków od matematyków z Europy kontynentalnej, ze szkodą dla matematyki angielskiej. Dokładna analiza prac Leibniza i Newtona pokazuje, że doszli do swoich wyników niezależnie, przy czym Leibniz zaczynał od całkowania, a Newton od różniczkowania. Jednak to Leibniz nadał nowej dyscyplinie nazwę. Newton nazwał swój rachunek różniczkowy „ nauką o strumieniach ”, termin ten przetrwał w angielskich szkołach do XIX wieku. Pierwszy kompletny traktat o rachunku różniczkowym napisany w języku angielskim i przy użyciu notacji Leibniza został opublikowany dopiero w 1815 roku.
Od czasów Leibniza i Newtona wielu matematyków przyczyniło się do ciągłego rozwoju rachunku różniczkowego. Jedna z pierwszych i najbardziej kompletnych prac dotyczących zarówno rachunku nieskończenie małych, jak i rachunku całkowego została napisana w 1748 roku przez Marię Gaetana Agnesi .
Podwaliny
W rachunku różniczkowym podstawy odnoszą się do rygorystycznego rozwoju przedmiotu z aksjomatów i definicji. We wczesnym rachunku różniczkowym używanie nieskończenie małych uważano za niekonsekwencję i było to ostro krytykowane przez wielu autorów, w szczególności Michela Rolle'a i biskupa Berkeleya . Berkeley opisał słynnie nieskończenie małe jako duchy odchodzących wielkości w swojej książce The Analyst w 1734 r. Wypracowanie rygorystycznych podstaw dla matematyków zajmujących się rachunkiem różniczkowym przez większą część stulecia po Newtonie i Leibnizie i nadal jest do pewnego stopnia aktywnym obszarem badań dzisiaj.
Kilku matematyków, w tym Maclaurin , próbowało udowodnić sensowność używania nieskończenie małych liczb, ale dopiero 150 lat później, dzięki pracom Cauchy'ego i Weierstrassa , ostatecznie znaleziono sposób na uniknięcie zwykłych „pojęć” o nieskończenie małych ilościach . Podstawy rachunku różniczkowego i całkowego zostały położone. Cours d'Analyse Cauchy'ego znajdujemy szeroki zakres fundamentalnych podejść, w tym definicję ciągłości w terminach nieskończenie małych i (nieco nieprecyzyjny) prototyp definicji (ε, δ) granicy w definicji różniczkowania. W swojej pracy Weierstrass sformalizował pojęcie granicy i wyeliminował nieskończenie małe (chociaż jego definicja może faktycznie potwierdzać nieskończenie małe kwadraty). Po pracach Weierstrassa ostatecznie powszechne stało się opieranie rachunku różniczkowego na granicach zamiast na wielkościach nieskończenie małych, chociaż temat ten jest nadal czasami nazywany „rachunkiem nieskończenie małym”. Bernhard Riemann wykorzystał te idee, aby podać dokładną definicję całki. Również w tym okresie idee rachunku różniczkowego zostały uogólnione na płaszczyznę zespoloną wraz z rozwojem analizy zespolonej .
We współczesnej matematyce podstawy rachunku różniczkowego zalicza się do dziedziny analizy rzeczywistej , która zawiera pełne definicje i dowody twierdzeń rachunku różniczkowego. Zasięg rachunku różniczkowego również został znacznie rozszerzony. Henri Lebesgue wynalazł teorię miary , opartą na wcześniejszych opracowaniach Émile'a Borela , i użył jej do zdefiniowania całek wszystkich funkcji poza najbardziej patologicznymi . Laurent Schwartz wprowadził rozkłady , za pomocą których można obliczyć pochodną dowolnej funkcji.
Granice nie są jedynym rygorystycznym podejściem do podstaw rachunku różniczkowego. Innym sposobem jest skorzystanie z niestandardowej analizy Abrahama Robinsona . Podejście Robinsona, opracowane w latach sześćdziesiątych XX wieku, wykorzystuje maszynerię techniczną z logiki matematycznej do rozszerzenia systemu liczb rzeczywistych o liczby nieskończenie małe i nieskończone , tak jak w oryginalnej koncepcji Newtona-Leibniza. Otrzymane liczby nazywane są liczbami hiperrzeczywistymi i można ich użyć do stworzenia podobnego do Leibniza rozwinięcia zwykłych reguł rachunku różniczkowego. Istnieje również płynna analiza nieskończenie małych , która różni się od analizy niestandardowej tym, że nakazuje pomijanie nieskończenie małych o wyższej mocy podczas wyprowadzania. Opierając się na ideach FW Lawvere'a i wykorzystując metody teorii kategorii , płynna analiza nieskończenie małych traktuje wszystkie funkcje jako ciągłe i nie dające się wyrazić w kategoriach bytów dyskretnych . Jednym z aspektów tego sformułowania jest to, że prawo wyłączonego środka nie obowiązuje. Prawo wykluczonego środka jest również odrzucane w matematyce konstruktywnej , gałęzi matematyki, która nalega, aby dowody na istnienie liczby, funkcji lub innego obiektu matematycznego dawały konstrukcję obiektu. Przeformułowania rachunku różniczkowego w ramach konstruktywnych są na ogół częścią przedmiotu analizy konstruktywnej .
Znaczenie
Podczas gdy wiele koncepcji rachunku różniczkowego zostało opracowanych wcześniej w Grecji , Chinach , Indiach , Iraku, Persji i Japonii , użycie rachunku różniczkowego rozpoczęło się w Europie w XVII wieku, kiedy Newton i Leibniz opierali się na pracach wcześniejszych matematyków, aby przedstawić jego podstawowe zasady. Węgierski polityk John von Neumann napisał o tej pracy:
Rachunek różniczkowy był pierwszym osiągnięciem współczesnej matematyki i trudno przecenić jego znaczenie. Myślę, że bardziej jednoznacznie niż cokolwiek innego definiuje początek współczesnej matematyki, a system analizy matematycznej, będący jej logicznym rozwinięciem, nadal stanowi największy postęp techniczny w ścisłym myśleniu.
Zastosowania rachunku różniczkowego obejmują obliczenia obejmujące prędkość i przyspieszenie , nachylenie krzywej i optymalizację . Zastosowania rachunku całkowego obejmują obliczenia obejmujące powierzchnię, objętość , długość łuku , środek masy , pracę i ciśnienie . Bardziej zaawansowane zastosowania obejmują szeregi potęgowe i szeregi Fouriera .
Rachunek różniczkowy jest również używany do dokładniejszego zrozumienia natury przestrzeni, czasu i ruchu. Przez wieki matematycy i filozofowie zmagali się z paradoksami polegającymi na dzieleniu przez zero lub sumowaniu nieskończenie wielu liczb. Te pytania pojawiają się w badaniu ruchu i obszaru. Starożytny grecki filozof Zenon z Elei podał kilka słynnych przykładów takich paradoksów . Rachunek różniczkowy dostarcza narzędzi, zwłaszcza szeregów granicznych i nieskończonych , które rozwiązują paradoksy.
Zasady
Granice i nieskończenie małe
Rachunek różniczkowy jest zwykle rozwijany przez pracę z bardzo małymi ilościami. Historycznie rzecz biorąc, pierwszą metodą robienia tego były nieskończenie małe . Są to obiekty, które można traktować jak liczby rzeczywiste, ale które w pewnym sensie są „nieskończenie małe”. Na przykład liczba nieskończenie mała może być większa niż 0, ale mniejsza niż jakakolwiek liczba w sekwencji 1, 1/2, 1/3, ... a zatem mniejsza niż jakakolwiek dodatnia liczba rzeczywista . Z tego punktu widzenia rachunek różniczkowy jest zbiorem technik manipulowania nieskończenie małymi. symbole i są małe
Podejście nieskończenie małe wypadło z łask w XIX wieku, ponieważ trudno było sprecyzować pojęcie nieskończenie małego. Pod koniec XIX wieku nieskończenie małe zostały zastąpione w środowisku akademickim epsilon, delta do granic . Granice opisują zachowanie funkcji na określonym wejściu w kategoriach jej wartości na sąsiednich wejściach. Przechwytują zachowanie na małą skalę, wykorzystując wewnętrzną strukturę systemu liczb rzeczywistych (jako przestrzeń metryczną z najmniejszą górną granicą ). W tym leczeniu rachunek różniczkowy jest zbiorem technik manipulowania pewnymi granicami. Nieskończenie małe liczby są zastępowane ciągami coraz mniejszych liczb, a nieskończenie małe zachowanie funkcji znajduje się, przyjmując zachowanie ograniczające dla tych ciągów. Uważano, że granice zapewniają bardziej rygorystyczną podstawę rachunku różniczkowego iz tego powodu stały się standardowym podejściem w XX wieku. Jednak koncepcja nieskończenie małych odrodziła się w XX wieku wraz z wprowadzeniem niestandardowej analizy i płynnej analizy nieskończenie małych , co dostarczyło solidnych podstaw do manipulowania nieskończenie małymi.
Rachunek różniczkowy
Rachunek różniczkowy to nauka o definicji, właściwościach i zastosowaniach pochodnej funkcji . Proces znajdowania pochodnej nazywa się różniczkowaniem . Biorąc pod uwagę funkcję i punkt w dziedzinie, pochodna w tym punkcie jest sposobem kodowania zachowania funkcji na małą skalę w pobliżu tego punktu. Znalezienie pochodnej funkcji w każdym punkcie jej dziedziny umożliwia utworzenie nowej funkcji, zwanej funkcją pochodną lub po prostu pochodną funkcji pierwotnej. Formalnie pochodna jest operatorem liniowym , który przyjmuje funkcję jako dane wejściowe i generuje drugą funkcję jako wynik. Jest to bardziej abstrakcyjne niż wiele procesów badanych w elementarnej algebrze, gdzie funkcje zwykle wprowadzają liczbę i wyprowadzają inną liczbę. Na przykład, jeśli funkcja podwajająca ma dane wejściowe trzy, to wyprowadza sześć, a jeśli funkcja podwajająca ma dane wejściowe trzy, to wyprowadza dziewięć. Pochodna może jednak przyjąć funkcję kwadratu jako dane wejściowe. Oznacza to, że pochodna pobiera wszystkie informacje funkcji podnoszącej do kwadratu — na przykład, że dwa są wysyłane do czterech, trzy do dziewięciu, cztery do szesnastu itd. — i wykorzystuje te informacje do utworzenia innej funkcji. Funkcja utworzona przez zróżnicowanie funkcji podnoszącej do kwadratu okazuje się funkcją podwajającą.
Mówiąc dokładniej, „funkcję podwajającą” można oznaczyć jako g ( x ) = 2 x , a „funkcję podnoszącą do kwadratu” przez f ( x ) = x 2 . „Pochodna” przyjmuje teraz funkcję f ( x ) , zdefiniowaną wyrażeniem „ x 2 ”, jako dane wejściowe, czyli wszystkie informacje — na przykład, że dwa są wysyłane do czterech, trzy są wysyłane do dziewięciu, cztery są wysyłane do szesnastu i tak dalej — i wykorzystuje tę informację do wyprowadzenia innej funkcji, funkcji g ( x ) = 2 x , jak się okaże.
W notacji Lagrange'a symbolem pochodnej jest podobny do apostrofu znak zwany liczbą pierwszą . Zatem pochodna funkcji zwanej f jest oznaczana przez f′ , wymawiane jako „f prim” lub „f myślnik”. Na przykład, jeśli f ( x ) = x 2 jest funkcją podnoszącą do kwadratu, to f′ ( x ) = 2 x jest jej pochodną (funkcja podwajająca g z góry).
Jeśli dane wejściowe funkcji reprezentują czas, to pochodna reprezentuje zmianę względem czasu. Na przykład, jeśli f jest funkcją, która bierze czas jako dane wejściowe i daje położenie kuli w tym czasie jako wynik, to pochodna f jest zmianą położenia w czasie, to znaczy jest to prędkość piłka.
Jeśli funkcja jest liniowa (to znaczy, jeśli wykres funkcji jest linią prostą), to funkcję można zapisać jako y = mx + b , gdzie x jest zmienną niezależną, y jest zmienną zależną, b jest y - punkt przecięcia, oraz:
Daje to dokładną wartość nachylenia linii prostej. Jeśli jednak wykres funkcji nie jest linią prostą, wówczas zmiana y podzielona przez zmianę x jest różna. Pochodne nadają dokładne znaczenie pojęciu zmiany w produkcji w odniesieniu do zmiany wejściowej. Aby być konkretnym, niech f będzie funkcją i ustal punkt a w dziedzinie f . ( a , f ( a )) jest punktem na wykresie funkcji. Jeśli h jest liczbą bliską zeru, to a + h jest liczbą bliską a . Dlatego ( a + h , f ( a + h )) jest bliskie ( a , f ( a )) . Nachylenie między tymi dwoma punktami wynosi
To wyrażenie nazywa się ilorazem różnicowym . Linia przechodząca przez dwa punkty na krzywej nazywana jest sieczną , więc m jest nachyleniem siecznej między ( a , f ( a )) i ( a + h , f ( a + h )) . Linia sieczna jest jedynie przybliżeniem zachowania funkcji w punkcie a, ponieważ nie uwzględnia tego, co dzieje się między a i a + h . Nie jest możliwe wykrycie zachowania w a przez ustawienie h na zero, ponieważ wymagałoby to podzielenia przez zero , które jest niezdefiniowane. Pochodna jest definiowana przez przyjęcie granicy , ponieważ h dąży do zera, co oznacza, że uwzględnia zachowanie f dla wszystkich małych wartości h i wyodrębnia spójną wartość dla przypadku, gdy h jest równe zeru:
Z geometrycznego punktu widzenia pochodna jest nachyleniem linii stycznej do wykresu f w a . Linia styczna jest granicą siecznych linii, tak jak pochodna jest granicą ilorazów różnicowych. Z tego powodu pochodna jest czasami nazywana nachyleniem funkcji f .
Oto konkretny przykład, pochodna funkcji podnoszącej do kwadratu na wejściu 3. Niech f ( x ) = x 2 będzie funkcją podnoszącą do kwadratu.

Nachylenie prostej stycznej do funkcji kwadratowej w punkcie (3, 9) wynosi 6, to znaczy, że rośnie sześć razy szybciej niż w prawo. Opisany właśnie proces graniczny można przeprowadzić dla dowolnego punktu w dziedzinie funkcji kwadratowej. To definiuje funkcję pochodną funkcji do kwadratu lub w skrócie pochodną funkcji do kwadratu. Obliczenie podobne do powyższego pokazuje, że pochodną funkcji podnoszącej do kwadratu jest funkcja podwajająca.
Notacja Leibniza
Typowa notacja, wprowadzona przez Leibniza, dla pochodnej w powyższym przykładzie to
W podejściu opartym na granicach symbol dy / dx należy interpretować nie jako iloraz dwóch liczb, ale jako skrót obliczonej powyżej granicy. Leibniz zamierzał jednak reprezentować iloraz dwóch nieskończenie małych liczb, przy czym dy jest nieskończenie małą zmianą y spowodowaną nieskończenie małą zmianą dx zastosowaną do x . Możemy również myśleć o d / dx jako o operatorze różniczkowania, który przyjmuje funkcję jako dane wejściowe i daje inną funkcję, pochodną, jako wynik. Na przykład:
W tym zastosowaniu dx w mianowniku jest odczytywane jako „w odniesieniu do x ”. Innym przykładem poprawnej notacji może być:
Nawet jeśli rachunek różniczkowy jest rozwijany przy użyciu granic, a nie nieskończenie małych, często manipuluje się symbolami takimi jak dx i dy , tak jakby były liczbami rzeczywistymi; chociaż można uniknąć takich manipulacji, są one czasami notacyjnie wygodne w wyrażaniu operacji, takich jak całkowita pochodna .
Rachunek całkowy
Rachunek całkowy to badanie definicji, właściwości i zastosowań dwóch powiązanych pojęć, całki nieoznaczonej i całki oznaczonej . Proces znajdowania wartości całki nazywa się całkowaniem . Całka nieoznaczona, znana również jako funkcja pierwotna , jest działaniem odwrotnym do pochodnej. F jest całką nieoznaczoną f , gdy f jest pochodną F . (To użycie małych i wielkich liter dla funkcji i jej całki nieoznaczonej jest powszechne w rachunku różniczkowym.) Całka oznaczona wprowadza funkcję i wyprowadza liczbę, która daje algebraiczną sumę obszarów między wykresem wejścia a oś x . Techniczna definicja całki oznaczonej obejmuje granicę sumy pól prostokątów, zwaną sumą Riemanna .
Motywującym przykładem jest odległość przebyta w określonym czasie. Jeśli prędkość jest stała, potrzebne jest tylko mnożenie:
Ale jeśli prędkość się zmienia, konieczna jest bardziej zaawansowana metoda znajdowania odległości. Jedną z takich metod jest przybliżenie przebytej odległości przez podzielenie czasu na wiele krótkich odcinków czasu, a następnie pomnożenie czasu, jaki upłynął w każdym przedziale czasu, przez jedną z prędkości w tym przedziale, a następnie obliczenie sumy (suma Riemanna ) przybliżona odległość przebyta w każdym interwale. Podstawową ideą jest to, że jeśli upłynie tylko krótki czas, prędkość pozostanie mniej więcej taka sama. Jednak suma Riemanna daje tylko przybliżenie przebytej odległości. Musimy przyjąć granicę wszystkich takich sum Riemanna, aby znaleźć dokładną przebytą odległość.
Gdy prędkość jest stała, całkowitą odległość przebytą w danym przedziale czasu można obliczyć, mnożąc prędkość i czas. Na przykład podróż ze stałą prędkością 50 mil na godzinę przez 3 godziny daje całkowity dystans 150 mil. Wykreślenie prędkości w funkcji czasu daje prostokąt o wysokości równej prędkości i szerokości równej upływającemu czasowi. Dlatego iloczyn prędkości i czasu oblicza również prostokątny obszar pod (stałą) krzywą prędkości. Ten związek między obszarem pod krzywą a przebytą odległością można rozszerzyć na dowolny obszar o nieregularnym kształcie, wykazujący zmienną prędkość w danym okresie czasu. Jeśli f ( x ) reprezentuje prędkość zmieniającą się w czasie, odległość przebyta między czasami reprezentowanymi przez a i b jest polem obszaru między f ( x ) a osią x , między x = a i x = b .
Aby przybliżyć ten obszar, intuicyjną metodą byłoby podzielenie odległości między a i b na liczbę równych segmentów, których długość jest reprezentowana przez symbol Δ x . Dla każdego małego segmentu możemy wybrać jedną wartość funkcji f ( x ) . Nazwij tę wartość h . Wtedy pole prostokąta o podstawie Δ x i wysokości h daje drogę (czas Δ x pomnożony przez prędkość h ) przebytą w tym segmencie. Z każdym segmentem związana jest średnia wartość funkcji znajdującej się powyżej, f ( x ) = h . Suma wszystkich takich prostokątów daje przybliżenie pola powierzchni między osią a krzywą, które jest przybliżeniem całkowitej przebytej odległości. Mniejsza wartość Δ x da więcej prostokątów iw większości przypadków lepsze przybliżenie, ale aby uzyskać dokładną odpowiedź, musimy przyjąć granicę, gdy Δ x zbliża się do zera.
Symbolem integracji jest sumowanie wydłużone S jako . Całka oznaczona jest zapisana jako:
i jest odczytywane jako „całka od a do b z f -of- x względem x ”. Notacja Leibniza dx ma sugerować podzielenie obszaru pod krzywą na nieskończoną liczbę prostokątów, tak aby ich szerokość Δ x stała się nieskończenie małą dx .
Całka nieoznaczona lub funkcja pierwotna jest zapisana:
Funkcje różniące się tylko stałą mają tę samą pochodną i można wykazać, że funkcja pierwotna danej funkcji jest w rzeczywistości rodziną funkcji różniących się tylko stałą. Ponieważ pochodna funkcji y = x 2 + C , gdzie C jest dowolną stałą, wynosi y′ = 2 x , funkcja pierwotna tej ostatniej jest dana wzorem:
Nieokreślona stała C obecna w całce nieoznaczonej lub funkcji pierwotnej jest znana jako stała całkowania .
Podstawowe twierdzenie
Podstawowe twierdzenie rachunku różniczkowego mówi, że różniczkowanie i całkowanie są operacjami odwrotnymi. Dokładniej, wiąże wartości funkcji pierwotnych z całkami oznaczonymi. Ponieważ zwykle łatwiej jest obliczyć funkcję pierwotną niż zastosować definicję całki oznaczonej, podstawowe twierdzenie rachunku różniczkowego zapewnia praktyczny sposób obliczania całek oznaczonych. Można to również interpretować jako precyzyjne stwierdzenie faktu, że różniczkowanie jest odwrotnością całkowania.
Podstawowe twierdzenie rachunku różniczkowego brzmi: Jeśli funkcja f jest ciągła na przedziale [ a , b ] i jeśli F jest funkcją, której pochodną jest f na przedziale ( a , b ) , to
Ponadto dla każdego x w przedziale ( a , b ) ,
Ta świadomość, dokonana zarówno przez Newtona , jak i Leibniza , była kluczem do rozpowszechnienia wyników analiz po tym, jak ich praca stała się znana. (Stopień, w jakim Newton i Leibniz byli pod wpływem bezpośrednich poprzedników, a zwłaszcza to, czego Leibniz mógł się nauczyć z prac Izaaka Barrowa , jest trudny do określenia ze względu na spór o pierwszeństwo między nimi). Podstawowe twierdzenie zapewnia algebraiczną metodę obliczania wiele całek oznaczonych — bez wykonywania procesów granicznych — poprzez znajdowanie wzorów na funkcje pierwotne . Jest to również prototypowe rozwiązanie równania różniczkowego . Równania różniczkowe wiążą nieznaną funkcję z jej pochodnymi i są wszechobecne w naukach ścisłych.
Aplikacje

Rachunek różniczkowy znajduje zastosowanie w każdej dziedzinie nauk fizycznych, aktuarialnej , informatyce , statystyce , inżynierii , ekonomii , biznesie , medycynie , demografii oraz w innych dziedzinach wszędzie tam, gdzie istnieje możliwość matematycznego modelowania problemu i poszukiwanie optymalnego rozwiązania. Pozwala przejść od (niestałego) tempa zmian do całkowitej zmiany lub odwrotnie, a wiele razy badając problem, znamy jedno i próbujemy znaleźć drugie. Rachunek różniczkowy może być używany w połączeniu z innymi dyscyplinami matematycznymi. Na przykład można go użyć z algebrą liniową , aby znaleźć „najlepiej dopasowane” przybliżenie liniowe dla zbioru punktów w dziedzinie. Lub może być użyty w teorii prawdopodobieństwa do określenia wartości oczekiwanej ciągłej zmiennej losowej, biorąc pod uwagę funkcję gęstości prawdopodobieństwa . W geometrii analitycznej , badaniu wykresów funkcji, rachunek różniczkowy służy do znajdowania punktów wysokich i niskich (maksima i minima), punktów nachylenia, wklęsłości i przegięcia . Rachunek różniczkowy jest również używany do znajdowania przybliżonych rozwiązań równań; w praktyce jest to standardowy sposób rozwiązywania równań różniczkowych i znajdowania pierwiastków w większości aplikacji. Przykładami są metody, takie jak metoda Newtona , iteracja punktu stałego i przybliżenie liniowe . Na przykład statki kosmiczne wykorzystują odmianę metody Eulera do przybliżania zakrzywionych kursów w środowiskach o zerowej grawitacji.
Fizyka czyni szczególny użytek z rachunku różniczkowego; wszystkie koncepcje mechaniki klasycznej i elektromagnetyzmu są powiązane za pomocą rachunku różniczkowego. Masę obiektu o znanej gęstości , moment bezwładności obiektów oraz potencjalne energie wynikające z sił grawitacyjnych i elektromagnetycznych można znaleźć za pomocą rachunku różniczkowego. Przykładem zastosowania rachunku różniczkowego w mechanice jest drugie prawo dynamiki Newtona , które mówi, że pochodna pędu obiektu względem czasu jest równa działającej na niego wypadkowej sile . Alternatywnie, drugie prawo Newtona można wyrazić, mówiąc, że siła wypadkowa jest równa masie obiektu pomnożonej przez jego przyspieszenie , które jest pochodną prędkości po czasie, a zatem drugą pochodną położenia przestrzennego po czasie. Zaczynając od wiedzy o przyspieszeniu obiektu, używamy rachunku różniczkowego do wyznaczenia jego ścieżki.
elektromagnetyzmu Maxwella i ogólna teoria względności Einsteina są również wyrażone w języku rachunku różniczkowego. Chemia wykorzystuje również rachunek różniczkowy do określania szybkości reakcji i badania rozpadu promieniotwórczego. W biologii dynamika populacji zaczyna się od wskaźników reprodukcji i śmiertelności w celu modelowania zmian populacji.
Twierdzenie Greena , które podaje zależność między całką krzywoliniową wokół prostej zamkniętej krzywej C i całką podwójną po obszarze płaszczyzny D ograniczonym przez C, jest stosowane w przyrządzie zwanym planimetrem, który służy do obliczania pola powierzchni płaskiej powierzchnia na rysunku. Na przykład można go użyć do obliczenia powierzchni zajmowanej przez klomb o nieregularnym kształcie lub basen podczas projektowania układu działki.
W dziedzinie medycyny rachunek różniczkowy można wykorzystać do znalezienia optymalnego kąta rozgałęzienia naczynia krwionośnego, aby zmaksymalizować przepływ. Rachunek różniczkowy można zastosować, aby zrozumieć, jak szybko lek jest usuwany z organizmu lub jak szybko rośnie guz nowotworowy .
W ekonomii rachunek różniczkowy pozwala na określenie maksymalnego zysku, umożliwiając łatwe obliczenie zarówno kosztu krańcowego , jak i przychodu krańcowego .
Zobacz też
- Słowniczek rachunku różniczkowego
- Lista tematów rachunku różniczkowego
- Lista pochodnych i całek w rachunkach alternatywnych
- Lista tożsamości różniczkowych
- Publikacje w rachunku różniczkowym
- Tablica całek
Dalsza lektura
- Adams, Robert A. (1999). Rachunek: Kompletny kurs . ISBN 978-0-201-39607-2 .
- Albers, Donald J.; Anderson, Richard D.; Loftsgaarden, Don O., wyd. (1986). Programy licencjackie z matematyki i informatyki: badanie z lat 1985–1986 . Amerykańskie Stowarzyszenie Matematyczne.
- Anton, Howard; Bivens, Irl; Davis, Stephen (2002). rachunek różniczkowy . John Wiley and Sons Pte. Ltd. ISBN 978-81-265-1259-1 .
- Apostoł Tom M. (1967). Rachunek różniczkowy, tom 1, rachunek jednej zmiennej ze wstępem do algebry liniowej . Wileya. ISBN 978-0-471-00005-1 .
- Apostoł Tom M. (1969). Rachunek różniczkowy, tom 2, rachunek różniczkowy i algebra liniowa z aplikacjami . Wileya. ISBN 978-0-471-00007-5 .
- Dzwon, John Lane (1998). Elementarz analizy nieskończenie małej . Wydawnictwo Uniwersytetu Cambridge. ISBN 978-0-521-62401-5 . Używa syntetycznej geometrii różniczkowej i nilpotentnych nieskończenie małych.
- Boelkins, M. (2012). Rachunek aktywny: darmowy, otwarty tekst (PDF) . Zarchiwizowane od oryginału w dniu 30 maja 2013 r . Źródło 1 lutego 2013 r .
- Boyer, Carl Benjamin (1959) [1949]. Historia rachunku różniczkowego i jego rozwój koncepcyjny (red. Dover). Hafnera. ISBN 0-486-60509-4 .
- Cajori, Florian (wrzesień 1923). „Historia notacji rachunku różniczkowego”. Roczniki matematyki . 2. seria. 25 (1): 1–46. doi : 10.2307/1967725 . hdl : 2027/mdp.39015017345896 . JSTOR 1967725 .
- Courant, Richard (3 grudnia 1998). Wprowadzenie do rachunku różniczkowego i analizy 1 . ISBN 978-3-540-65058-4 .
- Gonick, Larry (2012). Animowany przewodnik po rachunku różniczkowym . Williama Morrowa. ISBN 978-0-061-68909-3 . OCLC 932781617 .
- Keisler, HJ (2000). Rachunek elementarny: podejście z wykorzystaniem nieskończoności . Pobrano 29 sierpnia 2010 z http://www.math.wisc.edu/~keisler/calc.html
- Landau, Edmund (2001). Rachunek różniczkowy i całkowy . Amerykańskie Towarzystwo Matematyczne . ISBN 0-8218-2830-4 .
- Lebiediew, Leonid P.; Chmura, Michael J. (2004). „Narzędzia rachunku różniczkowego”. Przybliżanie doskonałości: podróż matematyka do świata mechaniki . Wydawnictwo Uniwersytetu Princeton.
- Larson, Ron ; Edwards, Bruce H. (2010). Rachunek różniczkowy (wyd. 9). Brooks Cole Cengage Nauka. ISBN 978-0-547-16702-2 .
- McQuarrie, Donald A. (2003). Metody matematyczne dla naukowców i inżynierów . Książki naukowe uniwersyteckie. ISBN 978-1-891389-24-5 .
- Pickover, Urwisko (2003). Rachunek i pizza: matematyczna książka kucharska dla głodnych umysłów . ISBN 978-0-471-26987-8 .
- Salas, Saturnino L.; Hille, Einar ; Etgen, Garret J. (2007). Rachunek różniczkowy: jedna i kilka zmiennych (wyd. 10). Wiley'a . ISBN 978-0-471-69804-3 .
- Spivak, Michael (wrzesień 1994). Rachunek . Opublikuj albo zgiń wydawnictwo. ISBN 978-0-914098-89-8 .
- Steen, Lynn Arthur , wyd. (1988). Rachunek na nowe stulecie; Pompa, a nie filtr . Amerykańskie Stowarzyszenie Matematyczne . ISBN 0-88385-058-3 .
- Stewart, James (2012). Rachunek różniczkowy: Early Transcendentals (wyd. 7). Brooks Cole Cengage Nauka. ISBN 978-0-538-49790-9 .
- Tomasz, George Brinton ; Finney, Ross L.; Weir, Maurice D. (1996). Rachunek różniczkowy i geometria analityczna, część 1 . Addisona Wesleya. ISBN 978-0-201-53174-9 .
- Thomas, George B .; Weir, Maurice D.; Hass, Joel ; Giordano, Frank R. (2008). Rachunek różniczkowy (wyd. 11). Addison-Wesley. ISBN 978-0-321-48987-6 .
- Thompson, Silvanus P .; Gardner, Martin (1998). Łatwy rachunek różniczkowy . ISBN 978-0-312-18548-0 .
Linki zewnętrzne
- „Rachunek” , Encyklopedia matematyki , EMS Press , 2001 [1994]
- Weisstein, Eric W. „Rachunek różniczkowy” . MathWorld .
- Tematy dotyczące rachunku różniczkowego w PlanetMath .
- Calculus Made Easy (1914) Silvanus P. Thompson Pełny tekst w formacie PDF
- Rachunek na In Our Time w BBC
- Calculus.org: Strona Calculus na Uniwersytecie Kalifornijskim w Davis – zawiera zasoby i linki do innych stron
- Najwcześniejsze znane zastosowania niektórych słów matematyki: rachunek różniczkowy i analiza
- Rola rachunku różniczkowego w matematyce uniwersyteckiej z ERICDigests.org
- OpenCourseWare Rachunek z Massachusetts Institute of Technology
- Rachunek nieskończenie mały – artykuł o jego historycznym rozwoju, w Encyclopedia of Mathematics , wyd. Michiela Hazewinkela .
- Daniela Kleitmana z MIT. „Rachunek dla początkujących i artystów” .
- Materiały szkoleniowe z rachunku różniczkowego na stronie imomath.com
- (w języku angielskim i arabskim) The Excursion of Calculus , 1772
























