Kołyska Newtona

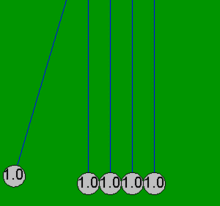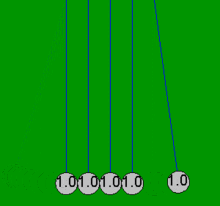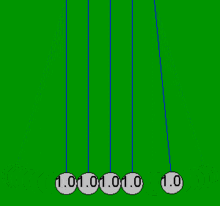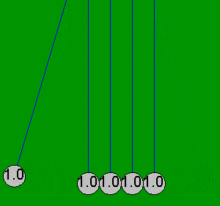
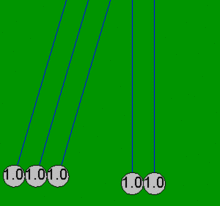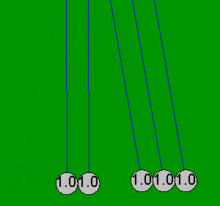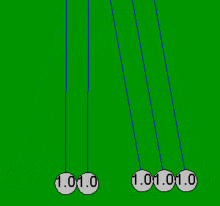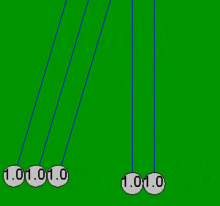
Kołyska Newtona to urządzenie, które demonstruje zachowanie pędu i zachowanie energii za pomocą kołyszących się kul. Kiedy jedna kula na końcu jest podnoszona i puszczana, uderza w nieruchome kule , przekazując siłę przez nieruchome kule, która popycha ostatnią kulę w górę. Ostatnia kula cofa się i uderza w prawie nieruchome kule, powtarzając efekt w przeciwnym kierunku. Urządzenie nosi imię XVII-wiecznego angielskiego naukowca Sir Isaaca Newtona i zostało zaprojektowane przez francuskiego naukowca Edme Mariotte . Jest również znany jako wahadło Newtona , kulki Newtona , wahadło Newtona lub klikacz kuli wykonawczej (ponieważ urządzenie wydaje kliknięcie za każdym razem, gdy kulki się zderzają, co robią wielokrotnie w stałym rytmie ).
Operacja
Kiedy jedna z końcowych kulek („pierwsza”) zostanie pociągnięta w bok, dołączony sznurek powoduje, że porusza się po łuku w górę. Kiedy jest puszczany, uderza w drugą piłkę i prawie się zatrzymuje. Piłka po przeciwnej stronie uzyskuje większość prędkości pierwszej piłki i kołysze się po łuku prawie tak wysoko, jak wysokość wypuszczenia pierwszej piłki. To pokazuje, że ostatnia piłka otrzymuje większość energii i pędu pierwszej piłki. Uderzenie wytwarza falę kompresji, która rozchodzi się przez kulki pośrednie. Robi to każdy efektywnie elastyczny materiał, taki jak stal, o ile ma energię kinetyczną jest tymczasowo magazynowana jako energia potencjalna podczas ściskania materiału, a nie tracona w postaci ciepła. Po początkowym uderzeniu wszystkie piłki poruszają się nieznacznie, ale ostatnia piłka otrzymuje większość początkowej energii z uderzenia pierwszej piłki. Kiedy dwie (lub trzy) kule zostaną upuszczone, dwie (lub trzy) kule po przeciwnej stronie odchylają się. Niektórzy twierdzą, że takie zachowanie demonstruje zachowanie pędu i energii kinetycznej w zderzeniach sprężystych. Jeśli jednak zderzające się kule zachowują się tak, jak opisano powyżej, przy tej samej masie mając tę samą prędkość przed i po zderzeniu, to w takim przypadku zachowana jest dowolna funkcja masy i prędkości.
Wyjaśnienie fizyki

Kołyskę Newtona można dość dokładnie modelować za pomocą prostych równań matematycznych przy założeniu, że kule zawsze zderzają się parami. Jeśli jedna piłka uderzy w cztery nieruchome kule, które już się stykają, te proste równania nie mogą wyjaśnić wynikowych ruchów we wszystkich pięciu piłkach, które nie są spowodowane stratami tarcia . Na przykład w prawdziwej kołysce Newtona czwarta kula ma pewien ruch, a pierwsza kula ma lekki ruch wsteczny. Wszystkie animacje w tym artykule pokazują wyidealizowaną akcję (proste rozwiązanie), która występuje tylko wtedy, gdy kule początkowo się nie stykają i zderzają tylko parami.
Proste rozwiązanie
Zasada zachowania pędu (masa × prędkość) i energii kinetycznej ( 1/2 × masa × prędkość 2 ) może być wykorzystana idealnie do znalezienia wynikowych prędkości dla dwóch zderzających się elastycznych obiektów . Te dwa równania służą do określenia wynikowych prędkości dwóch obiektów. W przypadku dwóch piłek ograniczonych do prostej ścieżki przez sznurki w kołysce, prędkości są pojedynczą liczbą zamiast wektora 3D dla przestrzeni 3D, więc matematyka wymaga tylko dwóch równań do rozwiązania dwóch niewiadomych. Kiedy dwa obiekty mają tę samą masę, rozwiązanie jest proste: poruszający się obiekt zatrzymuje się względem nieruchomego, a nieruchomy przejmuje całą początkową prędkość drugiego. Zakłada to doskonale sprężyste obiekty, więc nie ma potrzeby uwzględniania strat ciepła i energii akustycznej.
Stal nie ulega znacznej kompresji, ale jej elastyczność jest bardzo wydajna, więc nie powoduje dużych strat ciepła . Prosty efekt dwóch efektywnie sprężystych zderzających się obiektów o tej samej masie, ograniczonych do prostej ścieżki, jest podstawą efektu obserwowanego w kołysce i daje przybliżone rozwiązanie wszystkich jej działań.
W przypadku sekwencji elastycznych obiektów o tej samej masie ograniczonych do prostej ścieżki efekt dotyczy każdego kolejnego obiektu. Na przykład, gdy dwie piłki są upuszczane w celu uderzenia trzech nieruchomych piłek w kołysce, istnieje niezauważalna, ale kluczowa niewielka odległość między dwiema upuszczonymi piłkami, a działanie jest następujące: pierwsza poruszająca się piłka uderza w pierwszą nieruchomą piłkę (tzw. druga piłka uderza w trzecią piłkę) przenosi cały swój pęd na trzecią piłkę i zatrzymuje się. Następnie trzecia kula przenosi pęd na czwartą kulę i zatrzymuje się, a następnie czwarta na piątą kulę. Tuż za tą sekwencją znajduje się druga poruszająca się kula, przekazująca swój pęd pierwszej poruszającej się kuli, która właśnie się zatrzymała, a sekwencja powtarza się natychmiast i niezauważalnie za pierwszą sekwencją, wyrzucając czwartą piłkę tuż za piątą kulą z taką samą małą odległością, jak między dwie początkowe uderzające piłki. Jeśli po prostu dotykają się, gdy uderzają w trzecią piłkę, precyzja wymaga bardziej kompletnego rozwiązania poniżej.
Inne przykłady tego efektu
Efekt wyrzucenia ostatniej kuli z prędkością prawie równą pierwszej piłce można zobaczyć w przesuwaniu monety na stole w rząd identycznych monet, o ile uderzająca moneta i jej bliźniacze cele znajdują się w linii prostej. Efekt można podobnie zaobserwować w kulach bilardowych. Efekt można również zaobserwować, gdy ostra i silna fala ciśnienia uderza w gęsty jednorodny materiał zanurzony w mniej gęstym ośrodku . Jeśli identyczne atomy , cząsteczki , lub większe podobjętości gęstego jednorodnego materiału są przynajmniej częściowo elastycznie połączone ze sobą siłami elektrostatycznymi, mogą działać jak sekwencja zderzających się identycznych sprężystych kulek. Otaczające atomy, cząsteczki lub podobjętości doświadczające fali ciśnienia działają na siebie nawzajem, podobnie jak struna ogranicza kulki kołyski do linii prostej. Na przykład litotrypsji mogą być przesyłane przez skórę i tkankę bez uszkodzenia kamieni nerkowych . Strona kamieni przeciwna do nadchodzącej fali ciśnienia pęka, a nie strona otrzymująca początkowe uderzenie. W indyjskiej grze carrom napastnik zatrzymuje się po uderzeniu w stacjonarny element do gry, przenosząc cały swój pęd na uderzony element.
Kiedy stosuje się proste rozwiązanie
Aby proste rozwiązanie dokładnie przewidywało akcję, żadna para w trakcie zderzenia nie może dotknąć trzeciej bili, ponieważ obecność trzeciej bili skutecznie sprawia, że uderzona piłka wydaje się bardziej masywna. Zastosowanie dwóch równań zachowania do rozwiązania końcowych prędkości trzech lub więcej piłek w jednym zderzeniu daje wiele możliwych rozwiązań, więc te dwie zasady nie wystarczą do określenia wynikowego działania.
Nawet jeśli początkowa separacja jest niewielka, trzecia kula może wziąć udział w zderzeniu, jeśli początkowa separacja nie jest wystarczająco duża. W takim przypadku należy zastosować opisaną poniżej metodę kompletnego rozwiązania.
Małe stalowe kulki działają dobrze, ponieważ pozostają skutecznie elastyczne z niewielką utratą ciepła przy silnych uderzeniach i nie ściskają się zbytnio (do około 30 μm w małej kołysce Newtona). Małe, sztywne ściśnięcia oznaczają, że występują szybko, mniej niż 200 mikrosekund, więc stalowe kule mają większe szanse na zakończenie zderzenia, zanim dotkną pobliskiej trzeciej kuli. Bardziej miękkie elastyczne piłki wymagają większej separacji, aby zmaksymalizować efekt kolizji parami.
Bardziej kompletne rozwiązanie
Kołyska, która najlepiej pasuje do prostego rozwiązania, musi mieć początkową odległość między piłkami, która mierzy co najmniej dwukrotnie większą wartość, niż jakakolwiek z kulek, ale większość nie. Ta sekcja opisuje działanie, gdy początkowa separacja nie jest wystarczająca oraz w kolejnych zderzeniach, w których biorą udział więcej niż dwie piłki, nawet jeśli początkowa separacja. To rozwiązanie upraszcza się do prostego rozwiązania, gdy podczas zderzenia dotykają się tylko dwie kule. Dotyczy to wszystkich doskonale sprężystych identycznych kulek, które nie mają strat energii w wyniku tarcia i które można przybliżyć materiałami takimi jak stal, szkło, plastik i guma.
W przypadku zderzenia dwóch kul potrzebne są tylko dwa równania zachowania pędu i energii, aby rozwiązać dwie nieznane prędkości wynikowe. W przypadku trzech lub więcej zderzających się jednocześnie elastycznych kulek, względne ściśliwości zderzających się powierzchni są dodatkowymi zmiennymi, które określają wynik. Na przykład pięć piłek ma cztery punkty zderzenia, a skalowanie (dzielenie) trzech z nich przez czwartą daje trzy dodatkowe zmienne potrzebne do rozwiązania dla wszystkich pięciu prędkości po zderzeniu.
Działanie newtonowskie, lagranżowskie, hamiltonowskie i stacjonarne to różne sposoby matematycznego wyrażania mechaniki klasycznej . Opisują tę samą fizykę, ale muszą być rozwiązane różnymi metodami. Wszystkie wymuszają zachowanie energii i pędu. Prawo Newtona zostało wykorzystane w artykułach naukowych. Stosuje się go do każdej kuli, a suma sił jest równa zeru. Jest więc pięć równań, po jednym dla każdej kuli — i pięć niewiadomych, po jednym dla każdej prędkości. Jeśli kule są identyczne, bezwzględna ściśliwość powierzchni staje się nieistotna, ponieważ można ją podzielić z obu stron wszystkich pięciu równań, dając zero.
Wyznaczanie prędkości dla przypadku, gdy jedna piłka uderza w cztery początkowo stykające się piłki, można znaleźć, modelując piłki jako ciężarki z nietradycyjnymi sprężynami na ich zderzających się powierzchniach. Większość materiałów, takich jak stal, które są skutecznie elastyczne, w przybliżeniu jest zgodna z dotyczącym siły sprężyn , ale ponieważ powierzchnia styku kuli zwiększa się wraz ze wzrostem siły elastyczne kulki podążają za dopasowaniem Hertza do prawa Hooke'a, . To i prawo ruchu Newtona ( stosowane do każdej piłki, dając pięć prostych, ale współzależnych , są rozwiązywane numerycznie Kiedy piąta piłka zaczyna przyspieszać , otrzymuje pęd i energię z trzeciej i czwartej kuli poprzez sprężyste działanie ich ściśniętych powierzchni. W przypadku identycznych elastycznych piłek dowolnego typu, które początkowo dotykają piłek, działanie jest takie samo przy pierwszym uderzeniu, z tym wyjątkiem, że czas do zakończenia zderzenia wzrasta w przypadku miękkich materiałów. 40% do 50% energii kinetycznej początkowej piłki z uderzenia pojedynczej piłki jest magazynowane na powierzchniach piłki jako energia potencjalna przez większość procesu zderzenia. Czwartej piłce nadano 13% prędkości początkowej (co można postrzegać jako ruch o 3,3 stopnia, jeśli piąta kula przesunie się o 25 stopni), a pierwsze trzy kule mają niewielką prędkość odwrotną, przy czym pierwsza kula ma największy przy -7% prędkości początkowej. To oddziela piłki, ale wracają do siebie tuż przed powrotem piątej piłki. Jest to spowodowane zjawiskiem wahadła różnych małych zaburzeń kątowych mających w przybliżeniu ten sam czas powrotu do środka. Kiedy piłki „stykają się”
Równania różniczkowe Hertza przewidują, że jeśli dwie kule zderzą się z trzema, piąta i czwarta kula odlecą z prędkością 1,14 i 0,80 razy większą od prędkości początkowej. To 2,03 razy więcej energii kinetycznej w piątej piłce niż w czwartej kuli, co oznacza, że piąta kula wychylałaby się dwa razy wyżej w kierunku pionowym niż czwarta kula. Ale w prawdziwej kołysce Newtona czwarta kula wychyla się aż do piątej. Aby wyjaśnić różnicę między teorią a eksperymentem, dwie uderzające kule muszą być oddalone od siebie o co najmniej ≈ 10 μm (dla stali o masie 100 g i 1 m/s). Pokazuje to, że w powszechnym przypadku stalowych kul niezauważone separacje mogą być ważne i muszą być uwzględnione w równaniach różniczkowych Hertza, w przeciwnym razie proste rozwiązanie da dokładniejszy wynik.
Wpływ fal ciśnienia
Założono, że siły w powyższym rozwiązaniu Hertza rozchodzą się w kulkach natychmiast, co nie ma miejsca. Nagłe zmiany siły między atomami materiału tworzą falę ciśnienia. Fale ciśnienia (dźwięk) w stali przemieszczają się na odległość około 5 cm w ciągu 10 mikrosekund, czyli około 10 razy szybciej niż czas między uderzeniem pierwszej piłki a wyrzuceniem ostatniej piłki. Fale ciśnienia odbijają się tam iz powrotem przez wszystkie pięć kul około dziesięć razy, chociaż rozpraszają się do mniejszego czoła fali z większą liczbą odbić. Jest to wystarczająco szybkie, aby rozwiązanie Hertza nie wymagało istotnej modyfikacji w celu dostosowania do opóźnienia propagacji siły przez kulki. W mniej sztywnych, ale wciąż bardzo elastycznych kulkach, takich jak guma, prędkość propagacji jest mniejsza, ale czas trwania zderzeń jest dłuższy, więc nadal obowiązuje rozwiązanie Hertza. Błąd wprowadzony przez ograniczoną prędkość rozchodzenia się siły skłania rozwiązanie Hertza w kierunku rozwiązania prostego, ponieważ na zderzenia nie ma tak dużego wpływu bezwładność kulek znajdujących się dalej.
Identycznie ukształtowane kulki pomagają zbiegać się falom ciśnienia w punkcie styku ostatniej piłki: w początkowym punkcie uderzenia jedna fala ciśnienia idzie do przodu w kierunku innych piłek, a druga cofa się, odbijając się od przeciwnej strony pierwszej piłki, a następnie podąża za pierwszą falą, będąc dokładnie o 1 średnicę kuli za nim. Dwie fale spotykają się w ostatnim punkcie styku, ponieważ pierwsza fala odbija się od przeciwnej strony ostatniej piłki i spotyka się w ostatnim punkcie styku z drugą falą. Następnie odbijają się echem w tę iz powrotem około 10 razy, aż pierwsza kula przestanie łączyć się z drugą kulą. Następnie pogłos odbija się od punktu styku między drugą a trzecią kulą, ale nadal zbiega się w ostatnim punkcie styku, aż do wyrzucenia ostatniej kulki — ale z każdym odbiciem jest to mniej czoła fali.
Efekt różnych rodzajów piłek
Używanie różnych rodzajów materiałów nie zmienia działania, o ile materiał jest skutecznie elastyczny. Rozmiar kulek nie zmienia wyników, chyba że zwiększona waga przekracza granicę sprężystości materiału. Jeśli twarde kule są zbyt duże, energia jest tracona w postaci ciepła, ponieważ granica sprężystości wzrasta wraz z promieniem podniesionym do potęgi 1,5, ale energia, którą trzeba było pochłonąć i uwolnić, rośnie wraz z sześcianem promienia. Spłaszczenie powierzchni styku może w pewnym stopniu przezwyciężyć ten problem poprzez rozłożenie nacisku na większą ilość materiału, ale może to spowodować problem z wyrównaniem. Stal jest lepsza niż większość materiałów, ponieważ pozwala na częstsze stosowanie prostego rozwiązania w zderzeniach po pierwszym uderzeniu, jej zakres sprężystości do magazynowania energii pozostaje dobry pomimo wyższej energii spowodowanej jej ciężarem, a większa waga zmniejsza efekt oporu powietrza .
Używa
Najczęstszym zastosowaniem jest zabawka dla kadry kierowniczej na pulpicie . Innym zastosowaniem jest demonstracja fizyki edukacyjnej, jako przykład zachowania pędu i zachowania energii .
Historia
Zasada wykazana przez urządzenie, prawo zderzeń między ciałami, została po raz pierwszy zademonstrowana przez francuskiego fizyka Abbé Mariotte w XVII wieku. Jego praca na ten temat została po raz pierwszy przedstawiona Francuskiej Akademii Nauk w 1671 roku; został opublikowany w 1673 roku jako Traité de la percussion ou choc des corps („Traktat o perkusji lub wstrząsie ciał”).
Newton uznał pracę Mariotte'a, wraz z Wrenem, Wallisem i Huygensem, za pionierów eksperymentów dotyczących zderzeń kul wahadła w swoich Principia .
Christiaan Huygens używał wahadeł do badania zderzeń. Jego praca, De Motu Corporum ex Percussione (O ruchu ciał przez zderzenie), opublikowana pośmiertnie w 1703 r., Zawiera wersję pierwszego prawa Newtona i omawia zderzenie zawieszonych ciał, w tym dwóch ciał o równej masie, z ruchem poruszającego się ciała przeniesiony do tego, który jest w stanie spoczynku.
Istnieje wiele nieporozumień co do pochodzenia współczesnej kołyski Newtona. Marius J. Morin został uznany za pierwszego, który nazwał i stworzył tę popularną zabawkę dla kadry kierowniczej . [ potrzebne źródło ] Jednak na początku 1967 roku angielski aktor Simon Prebble ukuł nazwę „Kołyska Newtona” (obecnie używana ogólnie) dla drewnianej wersji produkowanej przez jego firmę, Scientific Demonstrations Ltd. Po początkowym oporze ze strony sprzedawców detalicznych, zostały po raz pierwszy sprzedane przez Harrodsa w Londynie, tworząc w ten sposób początek trwałego rynku zabawek dla kadry kierowniczej. [ potrzebne źródło ] Później rzeźbiarz i przyszły reżyser Richard Loncraine stworzył bardzo udany chromowany projekt sklepu Gear na Carnaby Street . [ potrzebne źródło ]
Największe urządzenie kołyskowe na świecie zostało zaprojektowane przez MythBusters i składało się z pięciu jednotonowych betonowych i stalowych boi wypełnionych prętami zbrojeniowymi , zawieszonych na stalowej kratownicy. Boje miały również stalową płytkę włożoną między ich dwie połówki, która działała jako „punkt kontaktowy” do przenoszenia energii; to urządzenie kołyskowe nie działało dobrze, ponieważ beton nie jest elastyczny, więc większość energii była tracona w wyniku gromadzenia się ciepła w betonie. Skonstruowana przez nich mniejsza wersja składa się z pięciu 15-centymetrowych (6 cali) łożysk kulkowych ze stali chromowanej, z których każde waży 15 kilogramów (33 funty) i jest prawie tak wydajna jak model stacjonarny.
Urządzenie kołyskowe z kulami kolizyjnymi o największej średnicy na wystawie publicznej było widoczne przez ponad rok w Milwaukee w stanie Wisconsin w sklepie detalicznym American Science and Surplus (patrz zdjęcie). Każda piłka była nadmuchiwaną piłką do ćwiczeń o średnicy 66 cm (26 cali) (obudowaną w stalowe pierścienie) i była podtrzymywana z sufitu za pomocą niezwykle silnych magnesów. Został zdemontowany na początku sierpnia 2010 roku z powodu problemów konserwacyjnych. [ potrzebne źródło ]
W kulturze popularnej
Kołyska Newtona była używana ponad 20 razy w filmach, często jako trop na biurku głównego złoczyńcy, na przykład rola Paula Newmana w The Hudsucker Proxy , Magneto w X-Men i Kryptonianie w Superman II . Był używany do reprezentowania nieugiętej pozycji NFL wobec urazów głowy w przypadku wstrząsu mózgu . Był również używany jako relaksująca rozrywka na biurku głównych inteligentnych / niespokojnych / wrażliwych postaci, takich jak rola Henry'ego Winklera w Nocnej zmianie , rola Dustina Hoffmana w Straw Dogs i rola Gwyneth Paltrow w Iron Man 2 . Zostało to bardziej widoczne jako seria glinianych garnków w Rosencrantz i Guildenstern Are Dead oraz jako rząd bąbelkowych krzeseł Eero Aarnio z 1968 roku ze skąpo odzianymi kobietami w Gamer . W Bocianach Hunter, dyrektor generalny Cornerstore, ma taki nie z piłkami, ale z małymi ptakami. Kołyska Newtona to przedmiot w Animal Crossing od Nintendo gdzie określa się ją jako „zabawkę wykonawczą”. W 2017 roku odcinek podcastu Omnibus z udziałem Jeopardy! mistrz Ken Jennings i muzyk John Roderick skupili się na historii Newton's Cradle. Kołyska Newtona znajduje się również na biurku zastępcy dyrektora ds. komunikacji Białego Domu Sama Seaborna w The West Wing . W odcinku Futuramy Dzień, w którym Ziemia stała się głupia (odcinek 7 sezonu 3), profesor Hubert Farnsworth jest pokazany z głową w kołysce Newtona i mówi, że jest geniuszem, gdy przechodzi obok Philip J. Fry.
Zespół rockowy Jefferson Airplane wykorzystał kołyskę na albumie Crown of Creation z 1968 roku jako urządzenie rytmiczne do tworzenia polirytmii w utworze instrumentalnym. [ potrzebne źródło ]
Zobacz też
Literatura
- Herrmann, F. (1981). „Proste wyjaśnienie dobrze znanego eksperymentu z kolizją” . American Journal of Physics . 49 (8): 761. Bibcode : 1981AmJPh..49..761H . doi : 10.1119/1.12407 .
- B. Brogliato: Mechanika niegładka. Modele, dynamika i kontrola , Springer, wydanie 2, 1999.
Linki zewnętrzne
- Szymanek, Donald (2020) [2001]. „Kołyska Newtona” . Uniwersytet Lock Haven . Zarchiwizowane od oryginału w dniu 9 października 2004 r.
- na YouTubie