Prawa ruchu Newtona

„Prawa Newtona” przekierowuje tutaj. W przypadku innych zastosowań zobacz prawo Newtona .

„F=ma” przekierowuje tutaj. Aby zapoznać się z konkursem fizycznym, zobacz Olimpiada Fizyczna Stanów Zjednoczonych .

Prawa ruchu Newtona, w połączeniu z jego prawem grawitacji, pozwalają przewidywać, jak planety , księżyce i inne obiekty krążą w Układzie Słonecznym , i są istotną częścią planowania podróży kosmicznych . Podczas Apollo 8 w 1968 roku astronauta Bill Anders zrobił to zdjęcie, Earthrise ; w drodze powrotnej na Ziemię Anders zauważył: „Myślę, że teraz większość jazdy prowadzi Isaac Newton ”.

Prawa ruchu Newtona to trzy podstawowe prawa mechaniki klasycznej , które opisują związek między ruchem obiektu a działającymi na niego siłami . Prawa te można sparafrazować w następujący sposób:

1. Ciało pozostaje w spoczynku lub porusza się ze stałą prędkością po linii prostej, chyba że działa na nie siła.
2. Kiedy na ciało działa siła, tempo zmian jego pędu w czasie jest równe sile.
3. Jeżeli dwa ciała działają na siebie siłami, to siły te mają tę samą wartość, ale przeciwne kierunki.

Trzy prawa ruchu zostały po raz pierwszy sformułowane przez Izaaka Newtona w jego Philosophiæ Naturalis Principia Mathematica ( Matematyczne zasady filozofii przyrody ), pierwotnie opublikowanej w 1687 r. Newton wykorzystał je do zbadania i wyjaśnienia ruchu wielu obiektów i układów fizycznych, które położyły podwaliny dla mechaniki klasycznej. Od czasu Newtona pojęciowa treść fizyki klasycznej została przeformułowana na alternatywne sposoby, z wykorzystaniem różnych podejść matematycznych, które dały wgląd, który był niejasny w oryginalnym, newtonowskim sformułowaniu. Odkryto również ograniczenia praw Newtona; potrzebne są nowe teorie, gdy obiekty poruszają się z bardzo dużymi prędkościami ( szczególna teoria względności ), są bardzo masywne ( ogólna teoria względności ) lub bardzo małe ( mechanika kwantowa ).

Wymagania wstępne

Prawa Newtona są często wyrażane w kategoriach mas punktowych lub cząstek , to znaczy ciał, których objętość jest pomijalna. Jest to rozsądne przybliżenie dla ciał rzeczywistych, gdy ruch części wewnętrznych można pominąć, a odległość między ciałami jest znacznie większa niż rozmiar każdego z nich. Na przykład Ziemię i Słońce można przybliżyć jako punktowe, biorąc pod uwagę orbitę pierwszego wokół drugiego, ale Ziemia nie jest punktowa, biorąc pod uwagę działania na jej powierzchni.

Matematyczny opis ruchu, czyli kinematyka , opiera się na idei określania pozycji za pomocą współrzędnych liczbowych. Ruch jest reprezentowany przez te liczby zmieniające się w czasie: trajektoria ciała jest reprezentowana przez funkcję, która przypisuje każdej wartości zmiennej czasu wartości wszystkich współrzędnych pozycji. Najprostszy przypadek jest jednowymiarowy, to znaczy gdy ciało jest zmuszone poruszać się tylko po linii prostej. Jego położenie można wtedy określić za pomocą pojedynczej liczby, wskazującej, gdzie jest względem wybranego punktu odniesienia. Na przykład ciało może swobodnie ślizgać się po torze biegnącym od lewej do prawej, więc jego położenie można określić na podstawie odległości od dogodnego punktu zerowego lub origin , przy czym liczby ujemne oznaczają pozycje po lewej stronie, a liczby dodatnie oznaczają pozycje po prawej. Jeśli położenie ciała w funkcji czasu wynosi ${1} }}$$jego$ średnia prędkość w przedziale czasu od 1 $t_$ jest

$${\ Displaystyle {\ Frac {\ Delta s} {\ Delta t}} = {\ Frac {s (t_ {1}) -s (t_ {0})} {t_ {1} -t_ {0}}} .}$$

Tutaj grecka litera $) jest używana, zgodnie z tradycją$ delta , w znaczeniu „zmiana”. Dodatnia średnia prędkość oznacza, że ​​​​współrzędna pozycji $}$ w danym przedziale, ujemna średnia prędkość wskazuje na spadek netto w tym przedziale, a średnia prędkość zerowa oznacza, że ​​​​ciało kończy przedział czasu w s {\ displaystyle s w tym samym miejscu, w którym się zaczęło. Rachunek daje środki do zdefiniowania chwilowego prędkość, miara prędkości i kierunku ruchu ciała w jednym momencie, a nie w przedziale czasu. Jednym z oznaczeń prędkości chwilowej jest zastąpienie $\ displaystyle$ przykład symbolem $\ Delta}$

$${\ displaystyle v = {\ frac {ds} {dt}}.}$$

Oznacza to, że prędkość chwilowa jest pochodną położenia względem czasu. Można $do$$w$ grubsza traktować jako stosunek między nieskończenie małą zmianą pozycji przedziału czasu, którym występuje. Dokładniej, prędkość i wszystkie inne pochodne można zdefiniować za pomocą pojęcia granicy . Funkcja ${\ displaystyle f (t)}$ ma granicę ${$$\ displaystyle L}$ przy danej wartości wejściowej , jeśli różnica między a $\$$displaystyle L }$ może być dowolnie mała, wybierając dane wejściowe wystarczająco bliskie $} \displaystyle t_{0}}$ . Jeden pisze,

$${\ Displaystyle \ lim _ {t \ do t_ {0}} f (t) = L.}$$

Prędkość chwilową można zdefiniować jako granicę średniej prędkości, gdy przedział czasu kurczy się do zera:

$${\ Displaystyle {\ Frac {ds} {dt}} = \ lim _ {\ Delta t \ do 0} {\ Frac {s (t + \ Delta t) -s (t)} {\ Delta t}}.}$$

Przyspieszenie ma się do prędkości tak, jak prędkość do położenia: jest pochodną prędkości względem czasu. Przyspieszenie można również zdefiniować jako granicę:

$${\ Displaystyle a = {\ Frac {dv} {dt}} = \ lim _ {\ Delta t \ do 0} {\ Frac {v (t + \ Delta t) -v (t)} {\ Delta t}} .}$$

W konsekwencji przyspieszenie jest drugą pochodną położenia, często zapisywaną. ${\ Displaystyle {\ Frac {d ^ {2} s} {dt ^ {2}}}$ }

Położenie, traktowane jako przemieszczenie od punktu początkowego, jest wektorem : wielkością, która ma zarówno wielkość, jak i kierunek. Prędkość i przyspieszenie również są wielkościami wektorowymi. Matematyczne narzędzia algebry wektorowej umożliwiają opisanie ruchu w dwóch, trzech lub więcej wymiarach. $displaystyle {\ vec {s}}}$ są często oznaczane strzałką, jak w , lub pogrubioną czcionką, na przykład ${\$ . Często wektory są przedstawiane wizualnie jako strzałki, przy czym kierunek wektora jest kierunkiem strzałki, a wielkość wektora jest wskazywana przez długość strzałki. Liczbowo wektor można przedstawić jako listę; na przykład wektor prędkości ciała może być ${\ Displaystyle {\ vec {v}} = (\ operatorname {3 ~ m / s} \ operatorname {4 ~ SM} )}$ , wskazując, że porusza się z prędkością 3 metrów na sekundę wzdłuż osi poziomej i 4 metrów na sekundę wzdłuż osi pionowej. Ten sam ruch opisany w innym układzie współrzędnych będzie reprezentowany przez różne liczby, a algebry wektorowej można użyć do translacji między tymi alternatywami.

Fizyczna koncepcja siły czyni ilościową codzienną ideę pchania lub ciągnięcia. Siły w mechanice Newtona są często spowodowane przez sznurki i liny, tarcie, wysiłek mięśni, grawitację i tak dalej. Podobnie jak przemieszczenie, prędkość i przyspieszenie, siła jest wielkością wektorową.

Prawa

Pierwszy

Sztuczne satelity poruszają się po zakrzywionych orbitach , a nie po liniach prostych, ze względu na grawitację Ziemi .

Przetłumaczone z łaciny, pierwsze prawo Newtona brzmi:

Każde ciało pozostaje w stanie spoczynku lub ruchu jednostajnym po linii prostej, chyba że zostanie zmuszone do zmiany tego stanu przez działające na nie siły.

Pierwsze prawo Newtona wyraża zasadę bezwładności : naturalnym zachowaniem ciała jest poruszanie się po linii prostej ze stałą prędkością. W przypadku braku wpływów zewnętrznych ruch ciała zachowuje status quo.

Współczesne rozumienie pierwszego prawa Newtona jest takie, że żaden obserwator inercjalny nie jest uprzywilejowany w stosunku do innych. Koncepcja obserwatora bezwładnościowego czyni ilościową codzienną ideę braku odczuwania skutków ruchu. Na przykład osoba stojąca na ziemi i obserwująca przejeżdżający pociąg jest obserwatorem bezwładnościowym. Jeżeli obserwator na ziemi widzi pociąg poruszający się płynnie po linii prostej ze stałą prędkością, to pasażer siedzący w pociągu będzie również obserwatorem inercyjnym: pasażer pociągu czuje się brak ruchu. Zasada wyrażona przez pierwsze prawo Newtona mówi, że nie można stwierdzić, który obserwator inercjalny „naprawdę” się porusza, a który „naprawdę” stoi w miejscu. Stan spoczynku jednego obserwatora jest stanem ruchu jednostajnego innego obserwatora po linii prostej i żaden eksperyment nie może uznać żadnego punktu widzenia za poprawny lub niepoprawny. Nie ma absolutnego standardu odpoczynku.

Drugi

Zmiana ruchu obiektu jest proporcjonalna do przyłożonej siły; i jest wykonywany w kierunku linii prostej, w której działa siła.

Przez „ruch” Newton miał na myśli wielkość zwaną teraz pędem , która zależy od ilości materii zawartej w ciele, prędkości, z jaką porusza się to ciało, oraz kierunku, w którym się porusza. We współczesnej notacji pęd ciała jest iloczynem jego masy i prędkości:

$${\ Displaystyle {\ vec {p}} = m {\ vec {v}} \,.}$$

Drugie prawo Newtona, we współczesnej formie, mówi, że pochodną czasu pędu jest siła:

$${\ Displaystyle {\ vec {F}} = {\ Frac {d {\ vec {p}}} {dt}} \,.}$$

Jeśli masa nie zmienia się w czasie, to pochodna działa tylko na prędkość, więc siła jest równa iloczynowi masy i pochodnej prędkości po czasie, czyli przyspieszeniu: m {\ displaystyle $}$

$${\ Displaystyle {\ vec {F}} = m {\ vec {a}} \,.}$$

Ponieważ przyspieszenie jest drugą pochodną położenia względem czasu, można to również zapisać

$${\ Displaystyle {\ vec {F}} = m {\ Frac {d ^ {2}} {dt ^ {2}}} {\ vec {s}} \,.}$$

Diagram swobodnego ciała dla klocka na pochyłej płaszczyźnie, ilustrujący siłę normalną prostopadłą do płaszczyzny ( N ), siłę grawitacji skierowaną w dół ( mg ) oraz siłę f wzdłuż kierunku płaszczyzny, którą można przykładowo zastosować , po sznurku.

Siły działające na ciało sumują się jako wektory , więc całkowita siła działająca na ciało zależy zarówno od wielkości, jak i od kierunku poszczególnych sił. Kiedy wypadkowa siła działająca na ciało jest równa zeru, to zgodnie z drugim prawem Newtona ciało nie przyspiesza i mówi się, że znajduje się ono w równowadze mechanicznej . Stan równowagi mechanicznej jest stabilny , jeśli przy niewielkiej zmianie położenia ciała ciało pozostaje blisko tej równowagi. W przeciwnym razie równowaga jest niestabilna.

Powszechną wizualną reprezentacją sił działających wspólnie jest diagram swobodnego ciała , który schematycznie przedstawia badane ciało i siły przyłożone do niego przez wpływy zewnętrzne. Na przykład schemat swobodnego ciała bloku znajdującego się na pochyłej płaszczyźnie może ilustrować kombinację siły grawitacji, siły „normalnej” , tarcia i naprężenia struny.

Drugie prawo Newtona jest czasami przedstawiane jako definicja siły, tj. siła to taka, która istnieje, gdy obserwator bezwładności widzi przyspieszające ciało. Aby to było czymś więcej niż tautologią — przyspieszenie implikuje siłę, siła implikuje przyspieszenie — należy również sformułować inne stwierdzenie dotyczące siły. Na przykład można określić równanie opisujące siłę, takie jak prawo powszechnego ciążenia Newtona . Wstawiając takie wyrażenie dla ${\ displaystyle {\ vec {F}}}$ do drugiego prawa Newtona można zapisać równanie o mocy predykcyjnej. Uznano również, że drugie prawo Newtona wyznacza program badawczy dla fizyki, ustalając, że ważnymi celami przedmiotu jest identyfikacja sił występujących w przyrodzie i skatalogowanie składników materii.

Trzeci

Każdemu działaniu zawsze przeciwstawia się równa reakcja; lub wzajemne oddziaływanie dwóch ciał na siebie jest zawsze równe i skierowane na przeciwne strony.

Rakiety działają poprzez wytwarzanie silnej siły reakcji skierowanej w dół za pomocą silników rakietowych . To popycha rakietę w górę, bez względu na ziemię lub atmosferę .

Zbyt krótkie parafrazy trzeciego prawa, takie jak „akcja równa się reakcji ”, mogły wywołać zamieszanie wśród pokoleń uczniów: „akcja” i „reakcja” odnoszą się do różnych ciał. Weźmy na przykład książkę leżącą na stole. Grawitacja Ziemi oddziałuje na książkę. „Reakcją” na to „działanie” nie jest siła podparcia ze stołu podtrzymującego książkę, ale przyciąganie grawitacyjne książki działające na Ziemię.

Trzecie prawo Newtona odnosi się do bardziej fundamentalnej zasady zachowania pędu . To ostatnie pozostaje prawdziwe nawet w przypadkach, w których stwierdzenie Newtona nie, na przykład, gdy pola siłowe , a także ciała materialne przenoszą pęd i gdy pęd jest właściwie zdefiniowany, również w mechanice kwantowej . W mechanice Newtona, jeśli dwa ciała mają odpowiednio pęd i ${\ Displaystyle {\ vec {p}} _ {1}},$ to p $\ Displaystyle {\ vec {p}} _ {2}}$ całkowity pęd pary wynosi ${\ Displaystyle {\ vec {p}} = {\ vec {p}} _ {1} + {\ vec {p}} _ {2}}$ i wskaźnik zmiana jest p $\ displaystyle {\ vec {p}}}$

$${\ Displaystyle {\ Frac {d {\ vec {p}}} {dt}} = {\ Frac {d {\ vec {p}} _ {1}} {dt}} + {\ Frac {d {\ vec {p}}_{2}}{dt}}.}$$

Zgodnie z drugim prawem Newtona, pierwszy człon to całkowita siła działająca na pierwsze ciało, a drugi człon to całkowita siła działająca na drugie ciało. Jeżeli dwa ciała są odizolowane od zewnętrznych wpływów, to na pierwsze ciało może oddziaływać jedynie siła działająca na drugie i odwrotnie. Zgodnie z trzecim prawem Newtona siły te mają taką samą wielkość, ale przeciwny kierunek, więc po dodaniu znoszą się, a ${\ displaystyle {\ vec {p}}}$ jest stałe. Alternatywnie $stała$ jeśli , wynika z tego, że siły mają taką samą wielkość i przeciwny kierunek.

Kandydaci do dodatkowych ustaw

Różne źródła proponowały podniesienie innych idei stosowanych w mechanice klasycznej do rangi praw Newtona. Na przykład w mechanice Newtona całkowita masa ciała utworzonego przez połączenie dwóch mniejszych ciał jest sumą ich indywidualnych mas. Frank Wilczek zasugerował zwrócenie uwagi na to założenie, nazywając je „prawem zerowym Newtona”. Innym kandydatem na „prawo zera” jest fakt, że w każdej chwili ciało reaguje na przyłożone do niego siły w tym momencie. Podobnie pomysł, że siły sumują się jak wektory (lub innymi słowy przestrzegają zasady superpozycji ) oraz pomysł, że siły zmieniają energię ciała, zostały opisane jako „czwarte prawo”.

Praca i energia

Fizycy rozwinęli koncepcję energii po czasach Newtona, ale stała się ona nieodłączną częścią tego, co uważa się za fizykę „newtonowską”. Energię można ogólnie podzielić na kinetyczną , związaną z ruchem ciała i potencjalną , związaną z położeniem ciała względem innych. Energia cieplna , energia przenoszona przez przepływ ciepła, jest rodzajem energii kinetycznej niezwiązanej z makroskopowym ruchem obiektów, ale z ruchami atomów i cząsteczek, z których są zbudowane. Zgodnie z twierdzeniem o pracy i energii , kiedy siła działa na ciało, gdy to ciało porusza się wzdłuż linii siły, siła działa na ciało, a ilość wykonanej pracy jest równa zmianie energii kinetycznej ciała. W wielu interesujących przypadkach praca wykonana przez siłę, gdy ciało porusza się w zamkniętej pętli — zaczynając od punktu, poruszając się wzdłuż pewnej trajektorii i wracając do punktu początkowego — wynosi zero. W takim przypadku siłę można zapisać jako gradient funkcji zwanej potencjałem skalarnym :

$${\ Displaystyle {\ vec {F}} = - {\ vec {\ nabla}} U \,.}$$

Dotyczy to wielu sił, w tym siły grawitacji, ale nie tarcia; w rzeczywistości prawie każdy problem w podręczniku mechaniki, który nie obejmuje tarcia, można wyrazić w ten sposób. Fakt, że siłę można zapisać w ten sposób, można zrozumieć z zasady zachowania energii . Bez tarcia rozpraszającego energię ciała w ciepło, energia ciała będzie wymieniać się między potencjalnymi i (nietermicznymi) formami kinetycznymi, podczas gdy całkowita ilość pozostaje stała. Każdemu przyrostowi energii kinetycznej, który występuje, gdy wypadkowa siła działająca na ciało przyspiesza je do większej prędkości, musi towarzyszyć utrata energii potencjalnej. Tak więc siła wypadkowa działająca na ciało jest określona przez sposób, w jaki maleje energia potencjalna.

Przykłady

Ruch jednostajnie przyspieszony

Główne artykuły: Swobodny spadek i Ruch pocisku

Skacząca piłka sfotografowana z szybkością 25 klatek na sekundę przy użyciu stroboskopowej lampy błyskowej . Pomiędzy odbiciami wysokość piłki w funkcji czasu jest zbliżona do paraboli , odchylającej się od łuku parabolicznego z powodu oporu powietrza, wirowania i deformacji w niekulisty kształt po uderzeniu.

Jeśli ciało spadnie ze stanu spoczynku w pobliżu powierzchni Ziemi, to przy braku oporu powietrza będzie przyspieszać ze stałą prędkością. Nazywa się to swobodnym spadkiem . Prędkość osiągnięta podczas swobodnego spadania jest proporcjonalna do upływającego czasu, a przebyta droga jest proporcjonalna do kwadratu upływającego czasu. Co ważne, przyspieszenie jest takie samo dla wszystkich ciał, niezależnie od ich masy. Wynika to z połączenia drugiego prawa dynamiki Newtona z jego prawem powszechnego ciążenia . Ten ostatni stwierdza, że ​​​​wielkość siły grawitacji z Ziemi na ciało wynosi

$${\ Displaystyle F = {\ Frac {GMm} {r ^ {2}}}}$$

gdzie $Ziemi$ masą spadającego ciała, $jest$$masą$ jest Newtona i $jest$ od środka Ziemi do położenia ciała, które jest bardzo bliskie promieniowi Ziemi. Ustawiając to na równą $\$ masa ciała anuluje się z obu stron równania, pozostawiając przyspieszenie zależne od m za { $}$${\ displaystyle G}$ , ${\ displaystyle M}$ i ${\ displaystyle r}$ i ${\ displaystyle r}$ można uznać za stałe. Ta konkretna wartość przyspieszenia jest zwykle oznaczana ${\ displaystyle g$ }

$${\ Displaystyle g = {\ Frac {GM} {r ^ {2}}} \ około \ operatorname {9,8 ~ m / s ^ {2}}.}$$

Jeśli ciało nie zostanie wypuszczone ze spoczynku, ale zamiast tego wyrzucone w górę i/lub poziomo z niezerową prędkością, wówczas swobodny spadek stanie się ruchem pocisku . Kiedy opór powietrza można pominąć, pociski poruszają się po paraboli , ponieważ grawitacja wpływa na ruch ciała w pionie, a nie w poziomie. W szczycie trajektorii pocisku jego prędkość pionowa wynosi zero, ale jego przyspieszenie jest $w$ dół, jak zawsze. Ustawienie niewłaściwego wektora równego zeru jest częstym nieporozumieniem wśród studentów fizyki.

Jednolity ruch kołowy

Główny artykuł: Ruch okrężny

Dwa obiekty poruszające się ruchem jednostajnym po okręgu, krążące wokół środka ciężkości (środek masy obu obiektów)

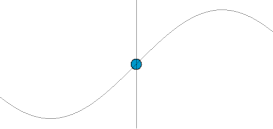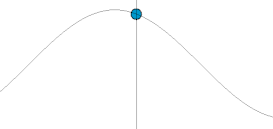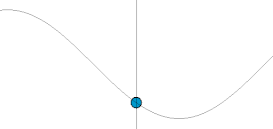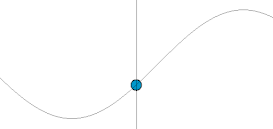
Kiedy ciało porusza się ruchem jednostajnym po okręgu, działająca na nie siła zmienia kierunek ruchu, ale nie prędkość. Dla ciała poruszającego się po okręgu o promieniu $}$${\ displaystyle r$ prędkością jego przyspieszenie ma wielkość r

$${\ Displaystyle a = {\ Frac {v ^ {2}} {r}}}$$

i jest skierowany w stronę środka okręgu. Siła wymagana do utrzymania tego przyspieszenia, zwana siłą dośrodkową , jest zatem również skierowana w stronę środka koła i ma wielkość ${\ Displaystyle mv ^ {2} / r}$ . Wiele orbit , takich jak orbita Księżyca wokół Ziemi, można przybliżyć ruchem jednostajnym po okręgu. W takich przypadkach siłą dośrodkową jest grawitacja, a zgodnie z prawem powszechnego ciążenia Newtona ma wielkość $.$$/ r ^ {2}}$ , gdzie jest masą większego ciała, które jest orbitowane Dlatego masę ciała można obliczyć na podstawie obserwacji innego ciała krążącego wokół niego.

Kula armatnia Newtona to eksperyment myślowy , który interpoluje między ruchem pocisku a ruchem jednostajnym po okręgu. Kula armatnia, która jest słabo odrzucona od krawędzi wysokiego urwiska, uderzy w ziemię w takim samym czasie, jak gdyby została zrzucona ze stanu spoczynku, ponieważ siła grawitacji wpływa tylko na pęd kuli armatniej w kierunku do dołu, a jej efekt jest nie zmniejszona przez ruch poziomy. Jeśli kula armatnia zostanie wystrzelona z większą początkową prędkością poziomą, to przeleci dalej, zanim uderzy w ziemię, ale nadal uderzy w ziemię w tym samym czasie. Jeśli jednak kula armatnia zostanie wystrzelona z jeszcze większą prędkością początkową, wówczas krzywizna Ziemi stanie się znacząca: sama ziemia zakrzywi się od spadającej kuli armatniej. Bardzo szybka kula armatnia wypadnie z inercyjnej trajektorii prostej z taką samą prędkością, z jaką Ziemia zakrzywia się pod nią; innymi słowy, będzie na orbicie (wyobrażając sobie, że nie jest spowalniany przez opór powietrza ani przeszkody).

Ruch harmoniczny

Główny artykuł: oscylator harmoniczny

Oscylator harmoniczny ze sprężyną masową

Prosty harmonijmy ruch

$x = 0}$ ciało o masie $, że$ do poruszania się wzdłuż osi i załóżmy punkt równowagi istnieje w pozycji $displaystyle$ . Oznacza to, że w $.$ wypadkowa działająca na ciało jest wektorem zerowym i zgodnie z drugim prawem Newtona ciało nie będzie przyspieszać Jeśli siła działająca na ciało jest proporcjonalna do wychylenia z punktu równowagi i skierowana do punktu równowagi, to ciało wykona prosty ruch harmoniczny . Zapisując siłę jako , drugie prawo Newtona staje się ${\ Displaystyle F = -kx}$

$${\ Displaystyle m {\ Frac {d ^ {2} x} {dt ^ {2}}} = - kx \,.}$$

To równanie różniczkowe ma rozwiązanie

$${\ Displaystyle x (t) = A \ sałata \ omega t + B \ sin \ omega t \,}$$

gdzie częstotliwość ${$ równa ${\ sqrt {k/m}}} ,$$\$$Displaystyle$ a stałe obliczyć znając , na przykład położenie i prędkość ciała w danym czasie, jak ${\ displaystyle t = 0}$ .

Jednym z powodów, dla których oscylator harmoniczny jest konceptualnie ważnym przykładem, jest to, że jest dobrym przybliżeniem dla wielu systemów w pobliżu stabilnej równowagi mechanicznej. Na przykład wahadło ma stabilną równowagę w pozycji pionowej: jeśli jest nieruchome, pozostanie tam, a lekko popchnięte będzie się kołysać w przód iw tył. Pomijając opór powietrza i tarcie w osi, siła działająca na wahadło to grawitacja, a drugie prawo Newtona staje się

$${\ Displaystyle {\ Frac {d ^ {2} \ teta} {dt ^ {2}}} = - {\ Frac {g} {L}} \ grzech \theta ,}$$

gdzie $jest$ długością wahadła i $pionu$ . Gdy kąt $\ theta}$ mały, sinus jest $prawie$ równy (patrz szereg Taylora , więc to wyrażenie upraszcza się do równania dla a θ $\ displaystyle$ prosty oscylator harmoniczny o częstotliwości ${\ Displaystyle \ omega = {\ sqrt {g / L}}}$ .

Oscylator harmoniczny może być tłumiony, często przez tarcie lub opór lepki, w którym to przypadku energia wypływa z oscylatora, a amplituda oscylacji maleje z czasem. Ponadto oscylator harmoniczny może być napędzany przyłożoną siłą, co może prowadzić do zjawiska rezonansu .

Obiekty o zmiennej masie

Główny artykuł: Układ o zmiennej masie

Rakiety, takie jak prom kosmiczny Atlantis , napędzają materię w jednym kierunku, aby popchnąć statek w drugim. Oznacza to, że pchana masa, rakieta i jej zapas paliwa na pokładzie stale się zmieniają.

Fizyka newtonowska traktuje materię jako nie stworzoną ani zniszczoną, chociaż można ją przeorganizować. Może się zdarzyć, że przedmiot zainteresowania zyskuje lub traci masę, ponieważ materia jest do niego dodawana lub z niego usuwana. W takiej sytuacji prawa Newtona można zastosować do poszczególnych kawałków materii, śledząc, które kawałki należą do przedmiotu zainteresowania w czasie. Na przykład, jeśli rakieta o masie $)$ poruszająca się z prędkością ${\ Displaystyle {\ vec {v}} (t)}$ prędkością wobec rakiety ${\ displaystyle {\ vec {u}}}$

$${\ Displaystyle {\ vec {F}} = M {\ Frac {d {\ vec {v}}} {dt}} - {\ vec { u}}{\frac {dM}{dt}}\,}$$

gdzie $wypadkową siłą zewnętrzną (np.$ grawitacyjnym planety).

Ruch i rotacja ciała sztywnego

Ciało sztywne to obiekt, którego rozmiar jest zbyt duży, aby go zaniedbać i który zachowuje ten sam kształt w czasie. W mechanice Newtona ruch ciała sztywnego jest często rozumiany przez rozdzielenie go na ruch środka masy ciała i ruch wokół środka masy.

Środek masy

Główny artykuł: Środek masy

Całkowity środek masy widelców , korka i wykałaczki znajduje się na czubku pióra

Znaczące aspekty ruchu rozciągniętego ciała można zrozumieć, wyobrażając sobie masę tego ciała skupioną w jednym punkcie, znanym jako środek masy. Położenie środka masy ciała zależy od tego, jak rozłożony jest materiał tego ciała. Dla zbioru obiektów punktowych o masach ${\ Displaystyle m_ {1}, \ ldots, m_ {N}}$ w pozycjach ${\ Displaystyle {\ vec {r }}_{1},\ldots,{\vec {r}}_{N}}$ , środek masy znajduje się w

$${\ Displaystyle {\ vec {R}} = \ suma _ {i = 1} ^ {N} {\ Frac {m_ {i} {\ vec { obręcz}},}$$

gdzie jest całkowitą masą $kolekcji$ W przypadku braku wypadkowej siły zewnętrznej środek masy porusza się ze stałą prędkością po linii prostej. Dotyczy to na przykład zderzenia dwóch ciał. Jeśli całkowita siła zewnętrzna jest różna od zera, to środek masy zmienia prędkość tak, jakby był ciałem punktowym o masie ${\ displaystyle M}$ . Wynika to z faktu, że siły wewnętrzne w zbiorze, siły, które przedmioty wywierają na siebie nawzajem, występują w zrównoważonych parach zgodnie z trzecim prawem Newtona. W układzie dwóch ciał, z których jedno jest znacznie masywniejsze od drugiego, środek masy będzie w przybliżeniu pokrywał się z położeniem masywniejszego ciała.

Obrotowe analogi praw Newtona

Kiedy prawa Newtona są stosowane do obracających się rozciągniętych ciał, prowadzą one do nowych wielkości, które są analogiczne do tych, na które powołano się w pierwotnych prawach. Odpowiednikiem masy jest moment bezwładności , odpowiednikiem pędu jest moment pędu , a odpowiednikiem siły jest moment obrotowy .

Moment pędu jest obliczany względem punktu odniesienia. Jeśli wektor przemieszczenia od punktu odniesienia do ciała wynosi ${\ displaystyle {\ vec {r}}},$ a ciało ma pęd , to moment pędu ciała z ${\ displaystyle {\ vec {p}}}$ w odniesieniu do tego punktu, używając iloczynu wektorowego ,

$${\ Displaystyle {\ vec {L}} = {\ vec {r}} \ razy {\ vec {p}}.}$$

Biorąc pochodną czasu momentu pędu daje

$${\ Displaystyle {\ Frac {d {\ vec {L}}} {dt}} = \ lewo ({\ Frac {d {\ vec {r}}} {dt}} \ prawej) \ razy {\ vec { p}}+{\vec {r}}\times {\frac {d{\vec {p}}}{dt}}={\vec {v}}\times m{\vec {v}}+{ \vec {r}}\times {\vec {F}}.}$$

Pierwszy wyraz $znika$ i $ten$ kierunek Pozostały termin to moment obrotowy,

$${\ Displaystyle {\ vec {\ tau}} = {\ vec {r}} \ razy {\ vec {F}}.}$$

Gdy moment obrotowy wynosi zero, moment pędu jest stały, podobnie jak gdy siła wynosi zero, pęd jest stały. Moment obrotowy może zniknąć nawet wtedy, gdy siła jest niezerowa, jeśli ciało znajduje się w punkcie odniesienia ( ) $fa$ jest $\ displaystyle {\ displaystyle {} \ vec {F}}}$ i wektor przemieszczenia $są$ tej samej linii.

Moment pędu zbioru mas punktowych, a tym samym rozciągniętego ciała, znajduje się poprzez dodanie wkładów z każdego z punktów. Zapewnia to sposób scharakteryzowania obrotu ciała wokół osi poprzez dodanie momentów pędu poszczególnych jego części. Wynik zależy od wybranej osi, kształtu ciała i prędkości obrotowej.

Wielociałowy układ grawitacyjny

Główne artykuły: Problem dwóch ciał i Problem trzech ciał

Animacja trzech punktów lub ciał przyciągających się do siebie

Prawo powszechnego ciążenia Newtona mówi, że każde ciało przyciąga każde inne ciało wzdłuż łączącej je linii prostej. Wielkość siły przyciągania jest proporcjonalna do iloczynu ich mas i odwrotnie proporcjonalna do kwadratu odległości między nimi. Znalezienie kształtu orbit, które stworzy prawo odwrotnych kwadratów sił, jest znane jako problem Keplera . Problem Keplera można rozwiązać na wiele sposobów, w tym poprzez wykazanie, że wektor Laplace'a – Runge – Lenza jest stała, lub stosując transformację dualności do dwuwymiarowego oscylatora harmonicznego. Jakkolwiek zostanie to rozwiązane, w rezultacie orbity będą przekrojami stożkowymi , to znaczy elipsami (w tym okręgami), parabolami lub hiperbolami . Ekscentryczność _ orbity, a tym samym typ przekroju stożkowego, jest określony przez energię i moment pędu orbitującego ciała. Planety nie mają wystarczającej energii, aby uciec od Słońca, dlatego ich orbity są elipsami z dobrym przybliżeniem; ponieważ planety przyciągają się nawzajem, rzeczywiste orbity nie są dokładnie przekrojami stożkowymi.

Jeśli doda się trzecią masę, problem Keplera staje się problemem trzech ciał, który na ogół nie ma dokładnego rozwiązania w postaci zamkniętej . Oznacza to, że nie ma sposobu, aby wyjść od równań różniczkowych implikowanych przez prawa Newtona i po skończonej sekwencji standardowych operacji matematycznych otrzymać równania, które wyrażają ruchy trzech ciał w czasie. Można zastosować metody numeryczne , aby uzyskać przydatne, choć przybliżone, wyniki dla problemu trzech ciał. Położenia i prędkości ciał mogą być przechowywane w zmiennych w pamięci komputera; Prawa Newtona są używane do obliczania, jak prędkości będą się zmieniać w krótkim przedziale czasu, a znając prędkości, można obliczyć zmiany położenia w tym przedziale czasu. Proces ten jest zapętlony w celu obliczenia w przybliżeniu trajektorii ciał. Ogólnie rzecz biorąc, im krótszy przedział czasu, tym dokładniejsze przybliżenie.

Chaos i nieprzewidywalność

Dynamika nieliniowa

Trzy podwójne wahadła, zainicjowane z prawie dokładnie takimi samymi warunkami początkowymi, rozchodzą się w czasie.

Główny artykuł: Teoria chaosu

Prawa ruchu Newtona dopuszczają możliwość chaosu . To znaczy, mówiąc jakościowo, układy fizyczne przestrzegające praw Newtona mogą wykazywać wrażliwą zależność od swoich warunków początkowych: niewielka zmiana położenia lub prędkości jednej części układu może doprowadzić do radykalnie odmiennego zachowania całego układu w krótkim czasie . Godne uwagi przykłady obejmują problem trzech ciał , podwójne wahadło , dynamiczny bilard i problem Fermiego – Pasty – Ulama – Tsingou .

Prawa Newtona można zastosować do płynów , rozważając płyn jako złożony z nieskończenie małych kawałków, z których każdy wywiera siły na sąsiednie kawałki. Równanie pędu Eulera jest wyrazem drugiego prawa Newtona dostosowanego do dynamiki płynów. Płyn jest opisany przez pole prędkości, tj. funkcję ${\ Displaystyle {\ vec {v}} ({\ vec {x}}, t)}$ który przypisuje wektor prędkości każdemu punktowi w czasie i przestrzeni. Mały obiekt unoszony przez przepływ płynu może zmienić prędkość z dwóch powodów: po pierwsze, ponieważ pole prędkości w jego położeniu zmienia się w czasie, a po drugie, ponieważ przemieszcza się do nowego miejsca, w którym pole prędkości ma inną wartość. W konsekwencji, gdy drugie prawo Newtona jest stosowane do nieskończenie małej części płynu, przyspieszenie ${\ displaystyle {\ vec {a}}}$ dwa wyrazy, kombinację znaną jako pochodna całkowita lub materialna za . Masa nieskończenie małej porcji zależy od gęstości płynu i działa na nią wypadkowa siła, jeśli ciśnienie płynu zmienia się z jednej strony na drugą. W związku z tym staje się za ${\ Displaystyle {\ vec {a}} = {\ vec {F}}/m$

$${\ Displaystyle {\ Frac {\ częściowe v} {\ częściowe t}} + ({\ vec {\ nabla }}\cdot {\vec {v}}){\vec {v}}=-{\frac {1}{\rho}}{\vec {\nabla}}P+{\vec {f}},}$$

gdzie to $grawitacyjne$ , $ciśnienie$$.$ a wpływ zewnętrzny, taki jak przyciąganie Uwzględnienie efektu lepkości zamienia równanie Eulera w równanie Naviera-Stokesa :

$${\ Displaystyle {\ Frac {\ częściowe v} {\ częściowe t}} + ( {\vec {\nabla}}\cdot {\vec {v}}){\vec {v}}=-{\frac {1}{\rho}}{\vec {\nabla}}P+\nu \ na bla ^{2}{\vec {v}}+{\vec {f}},}$$

gdzie jest $_$ kinematyczną .

Osobliwości

Jest matematycznie możliwe, aby zbiór mas punktowych poruszających się zgodnie z prawami Newtona wyrzucił niektóre z nich z taką siłą, że w skończonym czasie odleciały one w nieskończoność. To niefizyczne zachowanie, znane jako „niekolizyjność osobliwości”, zależy od tego, czy masy są punktowe i mogą zbliżać się do siebie dowolnie blisko, a także od braku relatywistycznego ograniczenia prędkości w fizyce newtonowskiej.

Nie wiadomo jeszcze, czy równania Eulera i Naviera-Stokesa wykazują analogiczne zachowanie początkowo gładkich rozwiązań „wysadzających się” w skończonym czasie. Kwestia istnienia i płynności rozwiązań Naviera-Stokesa jest jednym z problemów nagrody milenijnej .

Stosunek do innych sformułowań fizyki klasycznej

Mechanika klasyczna może być formułowana matematycznie na wiele różnych sposobów, innych niż opis „newtonowski” (który oczywiście zawiera wkład innych osób zarówno przed, jak i po Newtonie). Fizyczna zawartość tych różnych sformułowań jest taka sama jak Newtona, ale dostarczają one różnych spostrzeżeń i ułatwiają różne rodzaje obliczeń. Na przykład mechanika Lagrange'a pomaga uwidocznić związek między symetriami a prawami zachowania i jest przydatna przy obliczaniu ruchu ciał z ograniczeniami, takich jak masa ograniczona do poruszania się po zakrzywionym torze lub po powierzchni kuli. Mechanika hamiltonowska jest wygodna dla fizyki statystycznej , prowadzi do dalszego wglądu w symetrię i może być rozwinięta w wyrafinowane techniki teorii zaburzeń . Ze względu na rozległość tych tematów, dyskusja tutaj będzie ograniczona do zwięzłych omówień tego, w jaki sposób przeformułują one prawa ruchu Newtona.

Lagrange'a

Mechanika Lagrange'a różni się od sformułowania Newtona tym, że bierze pod uwagę całe trajektorie jednocześnie, zamiast przewidywać ruch ciała w jednej chwili. Tradycyjnie w mechanice Lagrange'a oznacza się pozycję za pomocą , ${\ kropka {q}}}$ prędkość za pomocą $Displaystyle$ . Najprostszym przykładem jest masywna cząstka punktowa, dla której Lagrange'a można zapisać jako różnicę między jej energią kinetyczną i potencjalną:

$${\ Displaystyle L (q, {\ kropka {q}}) = TV,}$$

gdzie jest energia kinetyczna

$${\ Displaystyle T = {\ Frac {1} {2}} m {\ kropka {q}} ^ {2}}$$

a energia potencjalna jest pewną funkcją położenia, ${\ Displaystyle V (q)}$ . Fizyczna ścieżka, którą cząstka pokona między punktem początkowym $displaystyle q_ {i}}$$jest$ , ścieżką, dla której całka Lagrange'a jest „stacjonarna” q ja { . Oznacza to, że ścieżka fizyczna ma tę właściwość, że małe jej perturbacje, w pierwszym przybliżeniu, nie zmienią całki Lagrange'a. Rachunek wariacyjny dostarcza narzędzi matematycznych do znajdowania tej ścieżki. Zastosowanie rachunku wariacyjnego do zadania znalezienia ścieżki daje równanie Eulera-Lagrange'a dla cząstki,

$${\ Displaystyle {\ Frac {d} {dt}} \ lewo ({\ Frac {\ częściowe L} {\ częściowe {\ kropka {q}}}} \ prawej) = {\ Frac {\ częściowe L} {\ częściowe q}}.}$$

Obliczanie pochodnych cząstkowych daje Lagrange'a

$$\ Displaystyle {\ Frac {d} {dt}} (m {\ kropka {q}}) = - {\ Frac {dV} {dq}} ,}$$

co jest powtórzeniem drugiego prawa Newtona. Lewa strona to pochodna pędu w czasie, a prawa strona to siła wyrażona jako energia potencjalna.

Landau i Lifshitz argumentują, że sformułowanie Lagrange'a czyni pojęciową treść mechaniki klasycznej jaśniejszą niż zaczynanie od praw Newtona. Mechanika Lagrange'a zapewnia wygodne ramy do udowodnienia twierdzenia Noether , które dotyczy symetrii i praw zachowania. Zachowanie pędu można wyprowadzić, stosując twierdzenie Noether do Lagrange'a dla układu wielocząstkowego, a zatem trzecie prawo Newtona jest raczej twierdzeniem niż założeniem.

Hamiltonian

Emmy Noether (1882–1935), która udowodniła słynne twierdzenie dotyczące symetrii i praw zachowania , kluczowe osiągnięcie we współczesnej fizyce, wygodnie wyrażone w języku mechaniki Lagrange'a lub Hamiltona.

W mechanice hamiltonowskiej dynamika układu jest reprezentowana przez funkcję zwaną hamiltonianem, która w wielu interesujących nas przypadkach jest równa całkowitej energii układu. Hamiltonian jest funkcją położeń i pędów wszystkich ciał tworzących układ, a także może wyraźnie zależeć od czasu. Pochodne czasowe zmiennych położenia i pędu są podane przez pochodne cząstkowe hamiltonianu za pomocą równań Hamiltona . Najprostszym przykładem jest masa punktowa ${\ displaystyle m}$ zmuszony do poruszania się po linii prostej pod wpływem potencjału. Pisząc dla współrzędnej pozycji i $displaystyle p}$ ciała, hamiltonian jest p $\$

$${\ Displaystyle {\ mathcal {H}} (p, q) = {\ Frac {p ^ {2}} {2m}} + V (q).}$$

W tym przykładzie równania Hamiltona są

$${\ Displaystyle {\ Frac {dq} {dt}} = {\ Frac {\ częściowe {\ mathcal {H}}} {\ częściowe p}}}$$

I

$${\ Displaystyle {\ Frac {dp} {dt}} = - {\ Frac {\ częściowe {\ mathcal {H}}} {\ częściowe q}}.}$$

Oceniając te pochodne cząstkowe, otrzymujemy poprzednie równanie

$${\ Displaystyle {\ Frac {dq} {dt}} = {\ Frac {p} {m}},}$$

który odtwarza znane stwierdzenie, że pęd ciała jest iloczynem jego masy i prędkości. Pochodna czasu pędu wynosi

$${\ Displaystyle {\ Frac {dp} {dt}} = - {\ Frac {dV} {dq}}}$$

co po utożsamieniu ujemnej pochodnej potencjału z siłą jest po prostu drugim prawem Newtona.

Podobnie jak w sformułowaniu Lagrange'a, w mechanice hamiltonowskiej zachowanie pędu można wyprowadzić za pomocą twierdzenia Noether, czyniąc trzecie prawo Newtona ideą, którą raczej się dedukuje niż zakłada.

Wśród propozycji zreformowania standardowego programu nauczania fizyki wprowadzającej jest taka, która uczy pojęcia energii przed pojęciem siły, zasadniczo „wstępnej mechaniki hamiltonowskiej”.

Hamilton-Jacobi

Hamiltona -Jacobiego zapewnia jeszcze jedno sformułowanie mechaniki klasycznej, które czyni je matematycznie analogicznym do optyki falowej . To sformułowanie również wykorzystuje funkcje hamiltonowskie, ale w inny sposób niż sformułowanie opisane powyżej. Ścieżki pokonywane przez ciała lub zbiory ciał są wyprowadzane z funkcji ${\ Displaystyle S ({\ vec {q}} _ {1}, {\ vec {q }}_{2},\ldots ,t)}$ pozycji ${\ displaystyle {\ vec {q}} _ {i}}$ i czas ${\ displaystyle t}$ . Hamiltonian jest włączony do równania Hamiltona-Jacobiego $,$ różniczkowego dla . Ciała poruszają się w czasie w taki sposób, że ich trajektorie są prostopadłe do powierzchni stałej $tego$ , jak promień światła rozchodzi się w kierunku prostopadłym do jego czoła fali. Najprościej można to wyrazić w przypadku pojedynczej masy punktowej, w której ${\ displaystyle S}$$się$$, a$ funkcją w kierunku, w którym stromo Innymi słowy, pęd masy punktowej jest gradientem S $\ displaystyle S}$ : S {\ displaystyle S }

$${\ Displaystyle {\ vec {v}} = {\ Frac {1} {m}} {\ vec {\ nabla}} S.}$$

Równanie Hamiltona-Jacobiego dla masy punktowej to

$${\ Displaystyle - {\ Frac {\ częściowe S} {\ częściowe t}} = H \ lewo ({\ vec {q}}, {\ vec {\ nabla}} S, t \ prawej).}$$

Związek z prawami Newtona można zobaczyć, rozważając masę punktową poruszającą się w potencjale niezależnym od czasu , w którym to przypadku równanie Hamiltona-Jacobiego staje się ${\ Displaystyle V ({\ vec {q}})}$

$${\ Displaystyle - {\ Frac {\ częściowe S} {\ częściowe t}} = {\ Frac {1} {2m}} \ lewo ({\ vec {\ nabla}} S \ prawej) ^ {2} + V ({\vec {q}}).}$$

Biorąc gradient po obu stronach, staje się to

$${\ Displaystyle - {\ vec {\ nabla}} {\ Frac {\ częściowe S} {\ częściowe t}} = {\ Frac {1} {2m}}} {\ vec {\ nabla}} \ lewo ({\ vec {\nabla}}S\right)^{2}+{\vec {\nabla}}V.}$$

Zamiana kolejności pochodnych cząstkowych po lewej stronie i użycie reguł potęgowych i łańcuchowych na pierwszym wyrazie po prawej stronie,

$${\ Displaystyle - {\ Frac {\ częściowy} {\ częściowy t}} {\ vec {\ nabla}} S = {\ Frac {1} {m}} \ lewo ({\ vec {\ nabla}} S \ cdot {\vec {\nabla}}\right){\vec {\nabla}}S+{\vec {\nabla}}V.}$$

Zbierając razem terminy, które zależą od gradientu , ${\ displaystyle S$ }

$${\ Displaystyle \ lewo [{\ Frac {\ częściowy} {\ częściowy t}} + {\ Frac {1} {m}} \ lewo ({\ vec {\ nabla}} S \ cdot {\ vec {\ nabla }}\right)\right]{\vec {\nabla}}S=-{\vec {\nabla}}V.}$$

Jest to kolejne powtórzenie drugiego prawa Newtona. Wyrażenie w nawiasach jest pochodną całkowitą lub materialną , jak wspomniano powyżej, w której pierwszy człon wskazuje, jak różniczkowana funkcja zmienia się w czasie w ustalonym miejscu, a drugi człon oddaje, w jaki sposób poruszająca się cząstka będzie widzieć różne wartości tej funkcji jako przemieszcza się z miejsca na miejsce:

$${\ Displaystyle \ lewo [{\ Frac {\ częściowe} {\ częściowe t}} + {\ Frac {1} {m}} \ lewo ({\ vec {\ nabla}} S \ cdot {\ vec {\ nabla }}\right)\right]=\left[{\frac {\częściowy }{\częściowy t}}+{\vec {v}}\cdot {\vec {\nabla}}\right]={\frac {d}{dt}}.}$$

Związek z innymi teoriami fizycznymi

Termodynamika i fizyka statystyczna

Symulacja większej, ale wciąż mikroskopijnej cząstki (na żółto) otoczonej gazem mniejszych cząstek, ilustrująca ruchy Browna .

W fizyce statystycznej kinetyczna teoria gazów stosuje prawa ruchu Newtona do dużej liczby (zwykle rzędu liczby Avogadra ) cząstek. Teoria kinetyki może na przykład wyjaśnić ciśnienie , jakie gaz wywiera na pojemnik, w którym się znajduje, jako zbiór wielu zderzeń atomów, z których każdy nadaje niewielką ilość pędu.

Równanie Langevina jest szczególnym przypadkiem drugiego prawa Newtona, przystosowanym do opisu małego obiektu bombardowanego stochastycznie przez jeszcze mniejsze. Można to napisać

$${\ Displaystyle m {\ vec {a}} = - \ gamma {\ vec {v}} + {\ vec {\ xi}} \,}$$

gdzie jest współczynnikiem oporu $i$ jest $.$ netto zderzeń z otaczającymi cząstkami Służy do modelowania ruchów Browna .

Elektromagnetyzm

Trzy prawa Newtona można zastosować do zjawisk związanych z elektrycznością i magnetyzmem , chociaż istnieją subtelności i zastrzeżenia.

Prawo Coulomba dotyczące siły elektrycznej między dwoma nieruchomymi, naładowanymi elektrycznie ciałami ma prawie taką samą postać matematyczną jak prawo powszechnego ciążenia Newtona: siła jest proporcjonalna do iloczynu ładunków, odwrotnie proporcjonalna do kwadratu odległości między nimi i skierowana wzdłuż linii prostej między nimi. Siła kulombowska, jaką ładunek ${2}}$ ładunek, $jest$ równa wielkości sile, którą $q_$$wskazuje$ na i dokładnie w przeciwnym kierunku Prawo Coulomba jest zatem zgodne z trzecim prawem Newtona.

Elektromagnetyzm traktuje siły jako wytwarzane przez pola działające na ładunki. Prawo siły Lorentza dostarcza wyrażenia na siłę działającą na naładowane ciało, którą można podłączyć do drugiego prawa Newtona w celu obliczenia jego przyspieszenia. Zgodnie z prawem siły Lorentza na naładowane ciało w polu elektrycznym działa siła skierowana w kierunku tego pola, siła proporcjonalna do jego ładunku $natężenia$ pola elektrycznego. Poza tym ruch naładowane ciało w polu magnetycznym działa siłą, która jest również proporcjonalna do jego ładunku, w kierunku prostopadłym zarówno do pola, jak i do kierunku ruchu ciała. Korzystając z wektorowego iloczynu krzyżowego ,

$${\ Displaystyle {\ vec {F}} = q {\ vec {E}} + q {\ vec {v}} \ razy {\ vec {B}}.}$$

Obowiązuje prawo siły Lorentza: pole magnetyczne zakrzywia elektrony po trajektorii kołowej.

Jeśli pole elektryczne zniknie ( $)$ siła będzie prostopadła do ruchu ładunku, tak jak w przypadku ruchu jednostajnego po okręgu badanego powyżej, a będzie krążyć (lub bardziej ogólnie poruszać się po helisie ) wokół linii pola magnetycznego z częstotliwością cyklotronu. ${\ displaystyle \ omega = qB/m}$ . Spekrtometria masy działa poprzez przyłożenie pól elektrycznych i/lub magnetycznych do poruszających się ładunków i pomiar wynikającego z tego przyspieszenia, które zgodnie z prawem siły Lorentza daje stosunek masy do ładunku .

Zbiory naładowanych ciał nie zawsze są zgodne z trzecim prawem Newtona: może nastąpić zmiana pędu jednego ciała bez kompensacyjnej zmiany pędu innego. Rozbieżność wynika z pędu przenoszonego przez samo pole elektromagnetyczne. Pęd na jednostkę objętości pola elektromagnetycznego jest proporcjonalny do wektora Poyntinga .

Istnieje subtelny koncepcyjny konflikt między elektromagnetyzmem a pierwszym prawem Newtona: teoria elektromagnetyzmu Maxwella przewiduje, że fale elektromagnetyczne będą przemieszczać się w pustej przestrzeni ze stałą, określoną prędkością. Tak więc niektórzy obserwatorzy inercjalni pozornie mają uprzywilejowany status w stosunku do innych, a mianowicie tych, którzy mierzą prędkość światła i znaleźć, że jest to wartość przewidziana przez równania Maxwella. Innymi słowy, światło zapewnia absolutny standard prędkości, jednak zasada bezwładności głosi, że nie powinno być takiego standardu. To napięcie zostaje rozwiązane w szczególnej teorii względności, która koryguje pojęcia przestrzeni i czasu w taki sposób, że wszyscy obserwatorzy inercjalni zgadzają się co do prędkości światła w próżni.

Szczególna teoria względności

W szczególnej teorii względności załamuje się zasada, którą Wilczek nazwał „zerowym prawem Newtona”: masa obiektu złożonego nie jest jedynie sumą mas poszczególnych elementów. Pierwsze prawo Newtona, ruch bezwładności, pozostaje prawdziwe. Obowiązuje również forma drugiego prawa Newtona, że ​​siła jest szybkością zmiany pędu, podobnie jak zasada zachowania pędu. Jednak definicja pędu jest zmodyfikowana. Jedną z konsekwencji tego jest fakt, że im szybciej ciało się porusza, tym trudniej jest je przyspieszyć, a więc bez względu na przyłożoną siłę ciało nie może zostać przyspieszone do prędkości światła. W zależności od problemu, pęd w szczególnej teorii względności można przedstawić jako wektor trójwymiarowy, ${\ Displaystyle {\ vec {p}} = m \ gamma {\ vec {v}}}$ , gdzie ${\ Displaystyle m} jest$ masą spoczynkową ciała i ${\ Displaystyle \ gamma}$ jest współczynnikiem Lorentza , który zależy od prędkości ciała. Alternatywnie, pęd i siłę można przedstawić jako cztery wektory .

Mechanika Newtona jest dobrym przybliżeniem szczególnej teorii względności, gdy zaangażowane prędkości są małe w porównaniu z prędkością światła.

Ogólna teoria względności

Ogólna teoria względności to teoria grawitacji, która wykracza poza teorię Newtona. W ogólnej teorii względności siła grawitacji jest ponownie wyobrażana jako zakrzywienie czasoprzestrzeni . Zakrzywiona ścieżka, taka jak orbita, nie jest wynikiem siły odchylającej ciało od idealnej linii prostej, ale raczej próbą ciała swobodnego opadania przez tło, które samo jest zakrzywione przez obecność innych mas. Uwaga Johna Archibalda Wheelera które stało się przysłowiowe wśród fizyków, podsumowuje teorię: „Czasoprzestrzeń mówi materii, jak się poruszać; materia mówi czasoprzestrzeni, jak się zakrzywiać”. Sam Wheeler uważał tę wzajemną zależność za współczesną, uogólnioną postać trzeciego prawa Newtona. Zależność między rozkładem materii a krzywizną czasoprzestrzeni jest określona przez równania pola Einsteina , które wymagają rachunku tensorowego do wyrażenia.

Newtonowska teoria grawitacji jest dobrym przybliżeniem przewidywań ogólnej teorii względności, gdy efekty grawitacyjne są słabe, a obiekty poruszają się powoli w porównaniu z prędkością światła.

Mechanika kwantowa

Mechanika kwantowa to teoria fizyki pierwotnie opracowana w celu zrozumienia zjawisk mikroskopowych: zachowania w skali cząsteczek, atomów lub cząstek subatomowych. Mówiąc ogólnie, im mniejszy jest system, tym bardziej odpowiedni model matematyczny będzie wymagał zrozumienia efektów kwantowych. Konceptualne podstawy fizyki kwantowej bardzo różnią się od podstaw fizyki klasycznej . Zamiast myśleć o wielkościach, takich jak położenie, pęd i energia, jako o właściwościach obiektu , należy zastanowić się, jaki wynik może się pojawić , gdy pomiar wykonywany jest wybrany typ. Mechanika kwantowa pozwala fizykowi obliczyć prawdopodobieństwo, że wybrany pomiar da określony wynik. Wartość oczekiwana pomiaru to średnia możliwych wyników, które może on dać, ważona prawdopodobieństwem ich wystąpienia.

Twierdzenie Ehrenfest zapewnia związek między kwantowymi wartościami oczekiwanymi a drugim prawem Newtona, związek, który z konieczności jest niedokładny, ponieważ fizyka kwantowa zasadniczo różni się od klasycznej. W fizyce kwantowej położenie i pęd są reprezentowane przez byty matematyczne znane jako operatory hermitowskie i reguła Borna służy do obliczania wartości oczekiwanych pomiaru pozycji lub pomiaru pędu. Te oczekiwane wartości będą na ogół zmieniać się w czasie; to znaczy, w zależności od czasu, w którym (na przykład) wykonywany jest pomiar pozycji, prawdopodobieństwa różnych możliwych wyników będą się różnić. Twierdzenie Ehrenfesta mówi, mówiąc z grubsza, że ​​równania opisujące, jak te wartości oczekiwane zmieniają się w czasie, mają postać przypominającą drugie prawo Newtona. Jednak im wyraźniejsze są efekty kwantowe w danej sytuacji, tym trudniej wyciągnąć sensowne wnioski z tego podobieństwa.

Historia

• 

  Isaac Newton (1643–1727), na portrecie Godfreya Knellera z 1689 r.

• 

  Własna kopia Newtona jego Principia , z odręcznymi poprawkami do drugiego wydania, w Bibliotece Wren w Trinity College w Cambridge

• 

  Pierwsze i drugie prawo Newtona, po łacinie, z oryginalnego Principia Mathematica z 1687 r.

Pojęcia przywołane w prawach ruchu Newtona — masa, prędkość, pęd, siła — miały swoich poprzedników we wcześniejszych pracach, a treść fizyki newtonowskiej została rozwinięta po czasach Newtona. Newton połączył wiedzę o ruchach ciał niebieskich z badaniem wydarzeń na Ziemi i wykazał, że jedna teoria mechaniki może obejmować obie.

Tło starożytności i średniowiecza

Przedmiot fizyki często wywodzi się od Arystotelesa ; jednak historia związanych z nimi koncepcji jest przesłonięta wieloma czynnikami. Dokładna zgodność między koncepcjami Arystotelesa i współczesnymi nie jest łatwa do ustalenia: Arystoteles nie rozróżniał jasno tego, co nazwalibyśmy prędkością i siłą, i użył tego samego terminu dla określenia gęstości i lepkości ; wyobrażał sobie ruch jak zawsze za pośrednictwem medium, a nie przestrzeni. Ponadto niektóre koncepcje często określane jako „arystotelesowskie” można lepiej przypisać jego naśladowcom i komentatorom. Komentatorzy ci stwierdzili, że fizyka Arystotelesa miała trudności z wyjaśnieniem ruchu pocisku. Arystoteles podzielił ruch na dwa typy: „naturalny” i „gwałtowny”. „Naturalnym” ruchem ziemskiej materii stałej było opadanie w dół, podczas gdy „gwałtowny” ruch mógł odepchnąć ciało na boki. Co więcej, w fizyce arystotelesowskiej „gwałtowny” ruch wymaga bezpośredniej przyczyny; oddzielone od przyczyny swojego „gwałtownego” ruchu, ciało powróciłoby do swojego „naturalnego” zachowania. Jednak oszczep porusza się dalej po tym, jak opuści rękę rzucającego. Arystoteles doszedł do wniosku, że powietrze wokół oszczepu musi mieć możliwość poruszania oszczepem do przodu. Jan Filopon , grecki myśliciel bizantyjski działający w VI wieku, uznał to za absurd: to samo medium, powietrze, było w jakiś sposób odpowiedzialne zarówno za podtrzymywanie ruchu, jak i za jego hamowanie. Gdyby pomysł Arystotelesa był prawdziwy, powiedział Filoponus, armie wystrzeliłyby broń, dmuchając na nie miechami. Filoponus argumentował, że wprawienie ciała w ruch nadaje jakość, impet , który byłby zawarty w samym ciele. Dopóki utrzymywał się jego impet, ciało poruszało się. W następnych stuleciach wersje teorii impulsu były rozwijane przez osoby, w tym Nur ad-Din al-Bitruji , Avicenna , Abu'l-Barakāt al-Baghdādī , John Buridan i Albert z Saksonii . Z perspektywy czasu idea impetu może być postrzegana jako prekursor nowoczesnej koncepcji pędu. (Intuicja, że ​​przedmioty poruszają się zgodnie z jakimś rodzajem impetu, utrzymuje się u wielu studentów fizyki wprowadzającej).

Bezwładność i pierwsze prawo

Nowoczesna koncepcja bezwładności jest przypisywana Galileuszowi . Na podstawie swoich eksperymentów Galileusz doszedł do wniosku, że „naturalnym” zachowaniem poruszającego się ciała jest poruszanie się, dopóki coś innego mu nie przeszkodzi. Galileo zauważył, że w ruchu pocisku grawitacja Ziemi wpływa na ruch pionowy, ale nie poziomy. Jednak idea bezwładności Galileusza nie była dokładnie tą, która zostałaby skodyfikowana w pierwszym prawie Newtona. Galileusz uważał, że ciało poruszające się bezwładnie na dużą odległość podążałoby za krzywizną Ziemi. Pomysł ten został poprawiony przez Isaaca Beeckmana , René Descartesa i Pierre Gassendi , który uznał, że ruch bezwładności powinien być ruchem prostoliniowym.

Siła i drugie prawo

Christiaan Huygens w swoim Horologium Oscillatorium (1673) wysunął hipotezę, że „Działaniem grawitacji, niezależnie od jej źródła, zdarza się, że ciała poruszają się ruchem składającym się zarówno z ruchu jednostajnego w jednym kierunku, jak i z ruchu ruch w dół pod wpływem grawitacji”. Drugie prawo Newtona uogólniło tę hipotezę z grawitacji na wszystkie siły.

Jedną z ważnych cech fizyki Newtona jest to, że siły mogą działać na odległość bez konieczności fizycznego kontaktu. Na przykład Słońce i Ziemia przyciągają się grawitacyjnie, mimo że dzielą je miliony kilometrów. Kontrastuje to z ideą, której bronił między innymi Kartezjusz, że grawitacja Słońca utrzymuje planety na orbicie, wirując je w wirze przezroczystej materii, eteru . Newton rozważał eteryczne wyjaśnienia siły, ale ostatecznie je odrzucił. Badanie magnetyzmu przez Williama Gilberta i innych stworzyło precedens dla myślenia o niematerialności siły i nie mogąc znaleźć zadowalającego ilościowo wyjaśnienia swojego prawa grawitacji w postaci modelu eteru, Newton w końcu oświadczył: „Nie stawiam żadnych hipotez ”: czy model taki jak wiry Kartezjusza może leżeć u podstaw teorii Principia , czy nie, czy też nie teorii ruchu i grawitacji, pierwszą podstawą do ich oceny muszą być ich udane przewidywania. I rzeczywiście, od czasów Newtona każda próba stworzenia takiego modelu kończyła się niepowodzeniem .

Zachowanie pędu i trzecie prawo

Johannes Kepler zasugerował, że przyciąganie grawitacyjne jest odwrotne — na przykład Księżyc przyciąga Ziemię, podczas gdy Ziemia przyciąga Księżyc — ale nie argumentował, że takie pary są równe i przeciwne. W swoich Zasadach filozofii (1644) Kartezjusz przedstawił ideę, że podczas zderzenia ciał „ilość ruchu” pozostaje niezmieniona. Kartezjusz zdefiniował tę wielkość nieco nieprecyzyjnie, dodając iloczyny prędkości i „rozmiaru” każdego ciała, gdzie „rozmiar” obejmował dla niego zarówno objętość, jak i pole powierzchni. Co więcej, Kartezjusz myślał o wszechświecie jako o plenum , to znaczy wypełnione materią, więc każdy ruch wymagał, aby ciało przemieszczało ośrodek podczas jego ruchu. W latach pięćdziesiątych XVII wieku Huygens badał zderzenia twardych kul i wydedukował zasadę, którą obecnie określa się jako zasadę zachowania pędu. Christopher Wren wydedukował później te same zasady dotyczące zderzeń sprężystych , jakie miał Huygens, a John Wallis zastosował zachowanie pędu do badania zderzeń niesprężystych . Newton zacytował prace Huygensa, Wrena i Wallisa, aby potwierdzić ważność swojego trzeciego prawa.

Newton doszedł do swojego zestawu trzech praw stopniowo. W rękopisie napisanym do Huygensa z 1684 roku wymienił cztery prawa: zasadę bezwładności, zmianę ruchu siłą, stwierdzenie o ruchu względnym, które dziś nazwalibyśmy niezmienniczością Galileusza , oraz zasadę, że interakcje między ciałami nie zmieniają ruchu ich środka masy. W późniejszym rękopisie Newton dodał prawo akcji i reakcji, mówiąc jednocześnie, że to prawo i prawo dotyczące środka masy implikują się nawzajem. Newton prawdopodobnie zdecydował się na prezentację w Principia, z trzema prawami pierwotnymi, a następnie innymi stwierdzeniami zredukowanymi do wniosków w 1685 r.

Po Principiach

Strona 157 z Mechanism of the Heavens (1831), rozszerzonej wersji Mary Somerville pierwszych dwóch tomów Traité de mécanique céleste Laplace'a. Tutaj Somerville wyprowadza prawo grawitacji odwrotnych kwadratów z praw ruchu planet Keplera .

Newton wyraził swoje drugie prawo, mówiąc, że siła działająca na ciało jest proporcjonalna do zmiany jego ruchu lub pędu. Zanim napisał Principia, rozwinął już rachunek różniczkowy (który nazwał „ nauką o strumieniach ”), ale w Principia nie zrobił z niego wyraźnego użytku, być może dlatego, że wierzył, że argumenty geometryczne w tradycji Euklidesa są bardziej rygorystyczne. W konsekwencji Principia nie wyraża przyspieszenia jako drugiej pochodnej położenia, a więc nie podaje drugiego prawa jako ${\ Displaystyle F = ma}$ . Ta forma drugiego prawa została napisana (dla szczególnego przypadku stałej siły) co najmniej już w 1716 r. Przez Jakoba Hermanna ; Leonhard Euler zastosował to jako podstawową przesłankę w latach czterdziestych XVIII wieku. Euler był pionierem w badaniu ciał sztywnych i ustanowił podstawową teorię dynamiki płynów. Pięciotomowa Traité de mécanique céleste Pierre-Simona Laplace'a (1798–1825) porzuciła geometrię i rozwinęła mechanikę wyłącznie za pomocą wyrażeń algebraicznych, rozwiązując jednocześnie pytania, które Principia pozostawił otwarte, jak pełna teoria przypływów .

Pojęcie energii stało się kluczową częścią mechaniki Newtona w okresie postnewtonowskim. Rozwiązanie Huygensa zderzenia twardych kul pokazało, że w tym przypadku zachowany jest nie tylko pęd, ale także energia kinetyczna (a raczej ilość, którą z perspektywy czasu możemy określić jako połowę całkowitej energii kinetycznej). Kwestia tego, co jest zachowane podczas wszystkich innych procesów, takich jak zderzenia nieelastyczne i ruch spowolniony przez tarcie, została rozwiązana dopiero w XIX wieku. Debaty na ten temat pokrywały się z filozoficznymi sporami między metafizycznymi poglądami Newtona i Leibniza, a warianty terminu „siła” były czasami używane do określenia tego, co nazwalibyśmy rodzajami energii. Na przykład w 1742 r. Émilie du Châtelet napisała: „Martwa siła składa się z prostej tendencji do ruchu: taka jest sprężyna gotowa do rozluźnienia; siła życiowa jest tym, co ciało ma, gdy jest w rzeczywistym ruchu. ”. We współczesnej terminologii „martwa siła” i „żyjąca siła” odpowiadają odpowiednio energii potencjalnej i energii kinetycznej. Zasada zachowania energii nie została uznana za uniwersalną zasadę, dopóki nie została zrozumiana że energia pracy mechanicznej może zostać rozproszona w ciepło.Z koncepcją energii, która ma solidne podstawy, prawa Newtona można następnie wyprowadzić w ramach sformułowań mechaniki klasycznej, które stawiają energię na pierwszym miejscu, jak w opisanych powyżej sformułowaniach Lagrange'a i Hamiltona.

Współczesne prezentacje praw Newtona wykorzystują matematykę wektorów, temat, który został rozwinięty dopiero pod koniec XIX i na początku XX wieku. Algebra wektorowa, zapoczątkowana przez Josiaha Willarda Gibbsa i Olivera Heaviside'a , wywodzi się z wcześniejszego systemu kwaternionów wymyślonego przez Williama Rowana Hamiltona iw dużej mierze go wyparła .

Zobacz też

• Historia mechaniki klasycznej
• Lista tytułowych praw
• Lista równań w mechanice klasycznej
• Lista praw naukowych nazwanych na cześć ludzi
• Wykaz podręczników mechaniki klasycznej i mechaniki kwantowej
• Kopuła Nortona

Dalsza lektura

• Chakrabarty, Deepto; Dourmaszkin, Piotr; Tomasz, Michelle; Frebel, Anna ; Vuletic, Vladan (2016). „Mechanika klasyczna” . MIT OpenCourseWare . Źródło 17 stycznia 2022 r .
• Thomson, W .; Tait, PG (1867). „242, prawa ruchu Newtona ”. Traktat o filozofii przyrody . Tom. 1.