Gęstość

Ten artykuł dotyczy gęstości masy. W przypadku innych zastosowań zobacz Gęstość (ujednoznacznienie) .

Gęstość
Probówka zawierająca cztery niemieszające się kolorowe ciecze o różnych gęstościach
Wspólne symbole	ρ , D
jednostka SI	kg/ m3
rozległe ?	NIE
Intensywny ?	Tak
Konserwowane ?	NIE
Pochodne z innych wielkości	${\ Displaystyle \ rho = {\ Frac {m} {V}}}$
Wymiar	${\ Displaystyle {\ mathsf {L}} ^ {- 3} {\ mathsf {M}}}$

Gęstość ( objętościowa gęstość masowa lub masa właściwa ) to masa substancji na jednostkę objętości . Najczęściej używanym symbolem oznaczającym gęstość jest ρ (mała grecka litera rho ), chociaż można również użyć łacińskiej litery D. Matematycznie gęstość definiuje się jako masę podzieloną przez objętość:

${\ Displaystyle \ rho = {\ Frac {m} {V}}}$

gdzie ρ to gęstość, m to masa, a V to objętość. W niektórych przypadkach (na przykład w przemyśle naftowym i gazowym w Stanach Zjednoczonych) gęstość jest luźno definiowana jako ciężar na jednostkę objętości , chociaż jest to naukowo niedokładne - ta wielkość jest dokładniej nazywana ciężarem właściwym .

Dla czystej substancji gęstość ma taką samą wartość liczbową jak jej stężenie masowe . Różne materiały mają zwykle różne gęstości, a gęstość może mieć znaczenie dla wyporności , czystości i opakowania . Osm i iryd to najgęstsze znane pierwiastki w standardowych warunkach temperatury i ciśnienia .

Aby uprościć porównywanie gęstości w różnych układach jednostek, czasami zastępuje się ją bezwymiarową wielkością „ gęstość względna ” lub „ ciężar właściwy ”, tj. stosunek gęstości materiału do gęstości materiału standardowego, zwykle wody. Zatem gęstość względna mniejsza niż jeden w stosunku do wody oznacza, że ​​substancja unosi się w wodzie.

Gęstość materiału zmienia się wraz z temperaturą i ciśnieniem. Ta zmienność jest zwykle niewielka w przypadku ciał stałych i cieczy, ale znacznie większa w przypadku gazów. Zwiększenie nacisku na obiekt zmniejsza objętość obiektu, a tym samym zwiększa jego gęstość. Podwyższenie temperatury substancji (z kilkoma wyjątkami) zmniejsza jej gęstość poprzez zwiększenie jej objętości. W większości materiałów ogrzewanie dna płynu powoduje konwekcję ciepła od dołu do góry, z powodu zmniejszenia gęstości ogrzanego płynu, co powoduje jego unoszenie się w stosunku do gęstszego nieogrzewanego materiału.

Odwrotność gęstości substancji jest czasami nazywana jej objętością właściwą , terminem używanym czasami w termodynamice . Gęstość jest właściwością intensywną , ponieważ zwiększenie ilości substancji nie zwiększa jej gęstości; raczej zwiększa swoją masę.

Inne koncepcyjnie porównywalne wielkości lub stosunki obejmują gęstość właściwą , gęstość względną (ciężar właściwy) i ciężar właściwy .

Historia

W znanej, ale zapewne apokryficznej opowieści Archimedesowi powierzono zadanie ustalenia, czy złotnik króla Hiero defraudował złoto podczas wytwarzania złotego wieńca poświęconego bogom i zastępowania go innym, tańszym stopem . Archimedes wiedział, że wieniec o nieregularnych kształtach można zmiażdżyć w sześcian, którego objętość można łatwo obliczyć i porównać z masą; ale król tego nie pochwalał. Mówi się, że zdumiony Archimedes wziął kąpiel zanurzeniową i zauważył, że woda podniosła się po wejściu, że może obliczyć objętość złotego wieńca na podstawie przemieszczenia wody . Po tym odkryciu wyskoczył z wanny i biegł nago ulicami, krzycząc: „Eureka! Eureka!” (Εύρηκα! Greckie „znalazłem to”). W rezultacie termin „ eureka ” wszedł do języka potocznego i jest używany do dziś, aby wskazać moment oświecenia.

Historia ta pojawiła się po raz pierwszy w formie pisemnej w księgach architektonicznych Witruwiusza , dwa wieki po tym, jak rzekomo miała miejsce. Niektórzy uczeni wątpili w dokładność tej opowieści, mówiąc między innymi, że metoda wymagałaby precyzyjnych pomiarów, które byłyby trudne do wykonania w tamtym czasie.

Pomiar gęstości

Istnieje wiele technik i standardów pomiaru gęstości materiałów. Techniki takie obejmują użycie areometru (metoda wyporu dla cieczy), wagi hydrostatycznej (metoda wyporu dla cieczy i ciał stałych), metody ciała zanurzonego (metoda wyporu dla cieczy), piknometru (dla cieczy i ciał stałych), piknometru porównawczego w powietrzu ( ciał stałych), densytometr oscylacyjny (ciecze), a także nalewanie i stukanie (ciała stałe). Jednak każda pojedyncza metoda lub technika mierzy różne rodzaje gęstości (np. gęstość nasypową, gęstość szkieletową itp.), dlatego konieczne jest zrozumienie typu mierzonej gęstości, jak również rodzaju danego materiału.

Jednostka

Z równania na gęstość ( ρ = m / V ) wynika, że ​​gęstość masy ma dowolną jednostkę będącą masą podzieloną przez objętość . Ponieważ istnieje wiele jednostek masy i objętości obejmujących wiele różnych wielkości, w użyciu jest duża liczba jednostek gęstości masy. Jednostka SI kilogram na metr sześcienny (kg/m ³ ) i jednostka cgs gram na centymetr sześcienny ( g /cm ³ ) są prawdopodobnie najczęściej używanymi jednostkami gęstości. Jeden g/cm ³ jest równy 1000 kg/m ³ . Jeden centymetr sześcienny (skrót cc) jest równy jednemu mililitrowi. W przemyśle inne większe lub mniejsze jednostki masy i/lub objętości są często bardziej praktyczne i można stosować zwyczajowe jednostki amerykańskie . Poniżej znajduje się lista niektórych z najpopularniejszych jednostek gęstości.

Jednorodne materiały

Gęstość we wszystkich punktach jednorodnego obiektu jest równa jego całkowitej masie podzielonej przez całkowitą objętość. Masę zwykle mierzy się za pomocą wagi lub wagi ; objętość można mierzyć bezpośrednio (z geometrii obiektu) lub przez przemieszczenie płynu. Do wyznaczenia gęstości cieczy lub gazu można użyć odpowiednio areometru , dazymetru lub przepływomierza Coriolisa . Podobnie ważenie hydrostatyczne wykorzystuje wypieranie wody przez zanurzony obiekt do określenia gęstości obiektu.

Materiały heterogeniczne

Jeśli ciało nie jest jednorodne, to jego gęstość zmienia się w różnych obszarach obiektu. W takim przypadku gęstość wokół dowolnego miejsca jest określana przez obliczenie gęstości małej objętości wokół tego miejsca. W granicy nieskończenie małej objętości gęstość niejednorodnego obiektu w punkcie wynosi: ${\ Displaystyle \ rho ({\ vec {r}}) = dm / dV}$ , gdzie ${\ displaystyle dV}$ to elementarna objętość na pozycji ${\ displaystyle r}$ . Masę ciała można więc wyrazić jako

${\ Displaystyle m = \ int _ {V} \ rho ({\ vec {r}}) \, dV.}$

Materiały niekompaktowe

W praktyce materiały sypkie, takie jak cukier, piasek czy śnieg, zawierają puste przestrzenie. Wiele materiałów występuje w przyrodzie w postaci płatków, peletek lub granulek.

Pustki to obszary, które zawierają coś innego niż rozważany materiał. Zwykle pustką jest powietrze, ale może to być również próżnia, ciecz, ciało stałe lub inny gaz lub mieszanina gazów.

Objętość nasypową materiału – łącznie z frakcją pustą – często uzyskuje się za pomocą prostego pomiaru (np. skalibrowaną miarką) lub geometrycznie ze znanych wymiarów.

Masa podzielona przez objętość nasypową określa gęstość nasypową . To nie to samo, co objętościowa gęstość masy.

Aby określić objętościową gęstość masy, należy najpierw odrzucić objętość frakcji pustej. Czasami można to określić za pomocą rozumowania geometrycznego. W przypadku ścisłego upakowania równych kulek frakcja niepustek może wynosić co najwyżej około 74%. Można to również ustalić empirycznie. Jednak niektóre materiały sypkie, takie jak piasek, mają zmienną frakcję pustych przestrzeni, która zależy od tego, jak materiał jest mieszany lub wlewany. Może być luźny lub zwarty, z większą lub mniejszą przestrzenią powietrzną w zależności od obsługi.

W praktyce frakcja pusta niekoniecznie jest powietrzem, a nawet gazem. W przypadku piasku może to być woda, co może być korzystne do pomiaru, ponieważ frakcja wolnych przestrzeni dla piasku nasyconego wodą — po dokładnym wypchnięciu wszelkich pęcherzyków powietrza — jest potencjalnie bardziej spójna niż suchy piasek mierzony z pustką powietrzną.

W przypadku materiałów niezwartych należy również zadbać o określenie masy próbki materiału. Jeśli materiał znajduje się pod ciśnieniem (zwykle jest to ciśnienie powietrza atmosferycznego na powierzchni ziemi), określenie masy na podstawie zmierzonej masy próbki może wymagać uwzględnienia efektu wyporu spowodowanego gęstością pustki, w zależności od sposobu przeprowadzenia pomiaru. W przypadku suchego piasku jest on na tyle gęstszy od powietrza, że ​​często pomija się efekt wyporu (mniej niż jedna część na tysiąc).

Zmiana masy po zastąpieniu jednego pustego materiału innym przy zachowaniu stałej objętości może być wykorzystana do oszacowania frakcji pustych przestrzeni, jeśli różnica gęstości dwóch pustych materiałów jest wiarygodnie znana.

Zmiany gęstości

Główne artykuły: ściśliwość i rozszerzalność cieplna

Ogólnie rzecz biorąc, gęstość można zmienić, zmieniając ciśnienie lub temperaturę . Zwiększenie ciśnienia zawsze zwiększa gęstość materiału. Podwyższenie temperatury generalnie zmniejsza gęstość, ale istnieją godne uwagi wyjątki od tego uogólnienia. Na przykład gęstość wody wzrasta między jej temperaturą topnienia w temperaturze 0 ° C a 4 ° C; podobne zachowanie obserwuje się w krzemie w niskich temperaturach.

   Wpływ ciśnienia i temperatury na gęstość cieczy i ciał stałych jest niewielki. Ściśliwość typowej cieczy lub ciała stałego wynosi 10-6 ^bar - ^{1 (1 bar =} 0,1 MPa), a typowa rozszerzalność cieplna wynosi 10-5 ^K - ¹ . Z grubsza przekłada się to na potrzebę około dziesięciu tysięcy razy ciśnienia atmosferycznego, aby zmniejszyć objętość substancji o jeden procent. (Chociaż potrzebne ciśnienie może być około tysiąc razy mniejsze w przypadku gleby piaszczystej i niektórych glin). Jednoprocentowe zwiększenie objętości zwykle wymaga wzrostu temperatury rzędu tysięcy stopni Celsjusza .

Natomiast gęstość gazów silnie zależy od ciśnienia. Gęstość gazu doskonałego wynosi

${\ Displaystyle \ rho = {\ Frac {MP} {RT}}}$

gdzie M to masa molowa , P to ciśnienie, R to uniwersalna stała gazowa , a T to temperatura bezwzględna . Oznacza to, że gęstość gazu doskonałego można podwoić, podwajając ciśnienie lub zmniejszając o połowę temperaturę bezwzględną.

W przypadku objętościowej rozszerzalności cieplnej przy stałym ciśnieniu i małych przedziałach temperatur zależność gęstości od temperatury wynosi

${\ Displaystyle \ rho = {\ Frac {\ rho _ {T_ {0}}} {1+ \ alfa \ cdot \ Delta T}}}$

gdzie jest $_ {$ w temperaturze odniesienia, jest współczynnikiem rozszerzalności cieplnej materiału w temperaturach bliskich $T_ {0}}} }}$$Displaystyle \$ .

Gęstość roztworów

Gęstość roztworu to suma stężeń masowych (masowych) składników tego roztworu.

Stężenie masowe (masowe) każdego danego składnika ρ _i w roztworze sumuje się do gęstości roztworu,

${\ Displaystyle \ rho = \ suma _ {i} \ varho _ {i}.}$

Wyrażona w funkcji gęstości czystych składników mieszaniny i ich udziału objętościowego pozwala na wyznaczenie nadmiarowych objętości molowych :

${\ Displaystyle \ rho = \ suma _ {i} \ rho _ { i}{\frac {V_{i}}{V}}\,=\sum _{i}\rho _{i}\varphi _{i}=\sum _{i}\rho _{i}{ \frac {V_{i}}{\sum _{i}V_{i}+\sum _{i}{V^{E}}_{i}}},}$

pod warunkiem, że nie ma interakcji między składnikami.

Znając zależność między nadmiarowymi objętościami a współczynnikami aktywności składników, można wyznaczyć współczynniki aktywności:

${\ Displaystyle {\ overline {V ^ {E}}} _ {i} = RT {\ Frac {\ częściowe \ ln \ gamma _ {i}} {\ częściowe P}}.}$

Gęstości

Różne materiały

Wybrane pierwiastki chemiczne są wymienione tutaj. Aby zapoznać się z gęstościami wszystkich pierwiastków chemicznych, zobacz Lista pierwiastków chemicznych

Gęstości różnych materiałów obejmujące zakres wartości

Materiał	ρ (kg/ m3 )	Notatki
Wodór	0,0898
Hel	0,179
aerografit	0,2
Metaliczna mikrosiatka	0,9
aerożel	1.0
Powietrze	1.2	Na poziomie morza
Sześciofluorek wolframu	12.4	Jeden z najcięższych znanych gazów w warunkach normalnych
Ciekły wodór	70	około godz. −255°C
Styropian	75	Około.
Korek	240	Około.
Sosna	373
Lit	535	Najmniej gęsty metal
Drewno	700	Dojrzały, typowy
Dąb	710
Potas	860
lód	916.7	W temperaturze < 0°C
Olej do gotowania	910–930
Sód	970
Woda (świeża)	1000	Przy 4 ° C temperatura jego maksymalnej gęstości
Woda (sól)	1030	3%
Ciekły tlen	1141	około godz. −219°C
Nylon	1150
Tworzywa sztuczne	1175	Około.; do polipropylenu i PETE / PVC
Glicerol	1261
tetrachloroeten	1622
Piasek	1600	Między 1600 a 2000
Magnez	1740
Beryl	1850
Krzem	2330
Beton	2400
Szkło	2500
kwarcyt	2600
Granit	2700
Gnejs	2700
Aluminium	2700
Wapień	2750	Kompaktowy
Bazalt	3000
Dijodometan	3325	Ciecz w temperaturze pokojowej
Diament	3500
Tytan	4540
Selen	4800
Wanad	6100
Antymon	6690
Cynk	7000
Chrom	7200
Cyna	7310
Mangan	7325	Około.
Żelazo	7870
stal miękka	7850
Niob	8570
Mosiądz	8600
Kadm	8650
Kobalt	8900
Nikiel	8900
Miedź	8940
Bizmut	9750
molibden	10220
Srebro	10500
Ołów	11340
Tor	11700
Rod	12410
Rtęć	13546
Tantal	16600
Uran	18800
Wolfram	19300
Złoto	19320
Pluton	19840
Ren	21020
Platyna	21.450
Iryd	22420
Osm	22570	Najgęstszy naturalny pierwiastek na Ziemi
Uwagi:

Inni

Podmiot	ρ (kg/ m3 )	Notatki
Ośrodek międzygwiezdny	1,7 × 10-26 _	Na podstawie 10-5 atomów wodoru na centymetr sześcienny
Lokalny Obłok Międzygwiezdny	5 × 10-22 _	Na podstawie 0,3 atomów wodoru na centymetr sześcienny
Ośrodek międzygwiezdny	1,7 × 10-16 _	W oparciu o 10 5 atomów wodoru na centymetr sześcienny
Ziemia _	5515	Średnia gęstość.
Wewnętrzne jądro Ziemi	13 000	W przybliżeniu, jak podano w Earth .
Jądro Słońca	33 000–160 000	Około.
Gwiazda białego karła	2,1 × 10 9	Około.
Jądra atomowe	2,3 × 10 17	Nie zależy silnie od wielkości jądra
Gwiazda neutronowa	1 × 10 18

Woda

Zobacz też: Gęstość wody

Gęstość wody w stanie ciekłym pod ciśnieniem 1 atm

Temp. (°C)	Gęstość (kg/m 3 )
−30	983.854
−20	993.547
−10	998.117
0	999.8395
4	999.9720
10	999.7026
15	999.1026
20	998.2071
22	997.7735
25	997.0479
30	995.6502
40	992.2
60	983.2
80	971,8
100	958,4
Uwagi:

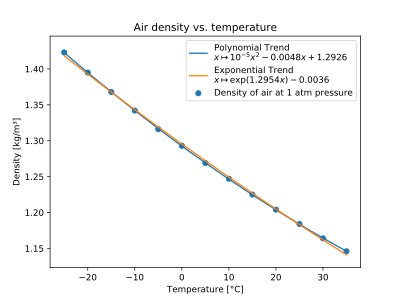
Powietrze

Główny artykuł: Gęstość powietrza

Gęstość powietrza a temperatura

Gęstość powietrza przy ciśnieniu 1 atm

T (°C)	ρ (kg/ m3 )
−25	1.423
−20	1.395
−15	1.368
−10	1.342
−5	1.316
0	1.293
5	1.269
10	1.247
15	1.225
20	1.204
25	1.184
30	1.164
35	1.146

Objętości molowe fazy ciekłej i stałej pierwiastków

Objętości molowe fazy ciekłej i stałej pierwiastków

Wspólne jednostki

Jednostką gęstości w układzie SI jest:

• kilogram na metr sześcienny (kg/m ³ )

Litr i tona nie są częścią SI, ale są dopuszczalne do użycia z nim, co prowadzi do następujących jednostek:

• kilogram na litr (kg/l)
• gram na mililitr (g/ml)
• tona na metr sześcienny (t/m ³ )

Gęstości przy użyciu następujących jednostek metrycznych mają dokładnie taką samą wartość liczbową, jedną tysięczną wartości w (kg/m ³ ). Woda w stanie ciekłym ma gęstość około 1 kg/dm ³ , co czyni każdą z tych jednostek SI liczbowo wygodną w użyciu, ponieważ większość ciał stałych i cieczy ma gęstość od 0,1 do 20 kg/dm ³ .

• kilogram na decymetr sześcienny (kg/dm ³ )
• gram na centymetr sześcienny (g/cm ³ )
  • 1 g/cm ³ = 1000 kg/m ³
• megagram (tona metryczna) na metr sześcienny (Mg/m ³ )

W USA zwyczajowe jednostki gęstości można określić w:

• Uncja avoirdupois na cal sześcienny (1 g/cm ³ ≈ 0,578036672 uncji/cu in)
• Uncja avoirdupois na uncję płynu (1 g/cm ³ ≈ 1,04317556 uncji/ uncji amerykańskiej = 1,04317556 funta/kufel amerykański)
• Avoirdupois funt na cal sześcienny (1 g/cm ³ ≈ 0,036127292 lb/cu in)
• funt na stopę sześcienną (1 g/cm3 ^≈ 62,427961 funta/stopę sześcienną)
• funt na jard sześcienny (1 g/cm3 ^≈ 1685,5549 funta/metr sześcienny)
• funt na galon cieczy amerykańskiej (1 g/cm3 ^≈ 8,34540445 funta/galona amerykańskiego)
• funt na buszel amerykański (1 g/cm ³ ≈ 77,6888513 lb/bu)
• ślimak na stopę sześcienną

Jednostki imperialne różniące się od powyższych (podobnie jak galon imperialny i buszel różnią się od jednostek amerykańskich) w praktyce są rzadko używane, chociaż można je znaleźć w starszych dokumentach. Galon imperialny opierał się na założeniu, że imperialna uncja wody miałaby masę jednej uncji Avoirdupois, a faktycznie 1 g/cm ³ ≈ 1,00224129 uncji na imperialną uncję płynu = 10,0224129 funtów na galon imperialny. Gęstość metali szlachetnych mogłaby być oparta na uncjach trojańskich i funtach, co może być przyczyną zamieszania.

Znając objętość komórki elementarnej materiału krystalicznego i jego wzór na masę (w daltonach ), można obliczyć gęstość. Jeden dalton na ångström sześcienny odpowiada gęstości 1,660 539 066 60 g/cm ³ .

Zobacz też

• Gęstości pierwiastków (strona danych)
• Lista pierwiastków według gęstości
• Gęstość powietrza
• Gęstość powierzchni
• Gęstość nasypowa
• Pławność
• Gęstość ładunku
• Przewidywanie gęstości metodą Girolamiego
• Dord
• Gęstość energii
• Lżejszy od powietrza
• Gęstość liniowa
• Gęstość liczb
• Gęstość ortobaryczna
• Gęstość papieru
• Dokładna waga
• Przyprawa (oceanografia)
• Standardowa temperatura i ciśnienie

Linki zewnętrzne

• „Gęstość” . Encyklopedia Britannica . Tom. 8 (wyd. 11). 1911.
• „Gęstość” . Praca referencyjna nowego ucznia   . 1914.
• Wideo: Eksperyment gęstości z olejem i alkoholem
• Wideo: Eksperyment gęstości z whisky i wodą
• Obliczanie gęstości szkła – Obliczanie gęstości szkła w temperaturze pokojowej i stopionego szkła w temperaturze 1000 – 1400°C
• Lista pierwiastków układu okresowego - posortowana według gęstości
• Obliczanie gęstości cieczy nasyconych dla niektórych składników
• Test gęstości pola
• Woda – Gęstość i ciężar właściwy
• Zależność gęstości wody od temperatury – Przeliczanie jednostek gęstości
• Pyszny eksperyment z gęstością
• Kalkulator gęstości wody Zarchiwizowano 13 lipca 2011 r. W Wayback Machine Gęstość wody dla danego zasolenia i temperatury.
• Kalkulator gęstości cieczy Wybierz ciecz z listy i oblicz gęstość w funkcji temperatury.
• Kalkulator gęstości gazu Oblicz gęstość gazu w funkcji temperatury i ciśnienia.
• Gęstości różnych materiałów.
• Wyznaczanie gęstości ciała stałego , instrukcja wykonania doświadczenia szkolnego.
• Lam EJ, Alvarez MN, Galvez ME, Alvarez EB (2008). „Model do obliczania gęstości wodnych wieloskładnikowych roztworów elektrolitów” . Dziennik chilijskiego Towarzystwa Chemicznego . 53 (1): 1393-8. doi : 10.4067/S0717-97072008000100015 .
•   Radović IR, Kijevčanin ML, Tasić AŽ, Djordjević BD, Šerbanović SP (2010). „Pochodne właściwości termodynamiczne mieszanin alkohol + cykloheksyloamina”. Dziennik Serbskiego Towarzystwa Chemicznego . 75 (2): 283–293. CiteSeerX 10.1.1.424.3486 . doi : 10.2298/JSC1002283R .