Gęstość energii

Ten artykuł dotyczy energii na jednostkę objętości. Aby uzyskać informacje na temat energii na jednostkę masy, zobacz Energia właściwa .
Gęstość energii
jednostka SI J / m 3
Inne jednostki
 J/L, W⋅h/L
W jednostkach podstawowych SI m −1 ⋅kg⋅s −2

Pochodne z innych wielkości
U = E / V
Wymiar

W fizyce gęstość energii to ilość energii zmagazynowanej w danym układzie lub obszarze przestrzeni na jednostkę objętości . Czasami jest mylona z energią na jednostkę masy , która jest właściwie nazywana energią właściwą lub grawimetryczną gęstością energii .

Często mierzona jest tylko energia użyteczna lub możliwa do wydobycia, co oznacza, że ​​energia niedostępna (taka jak energia masy spoczynkowej ) jest ignorowana. Jednak w kontekście kosmologicznym i innych ogólnych kontekstach relatywistycznych rozważane gęstości energii to te, które odpowiadają elementom tensora naprężenia-energii , a zatem obejmują energię masy, jak również gęstości energii związane z ciśnieniem .

Energia na jednostkę objętości ma takie same jednostki fizyczne jak ciśnienie iw wielu sytuacjach jest synonimem . Na przykład gęstość energii pola magnetycznego może być wyrażona jako ciśnienie fizyczne i zachowuje się jak ciśnienie. Podobnie energię potrzebną do sprężenia gazu do określonej objętości można określić, mnożąc różnicę między ciśnieniem gazu a ciśnieniem zewnętrznym przez zmianę objętości. Gradient ciśnienia opisuje potencjał do wykonania pracy nad otoczeniem poprzez zamianę energii wewnętrznej na pracę, aż do osiągnięcia równowagi.

Przegląd

Istnieją różne rodzaje energii magazynowanej w materiałach, a uwolnienie każdego rodzaju energii wymaga szczególnego rodzaju reakcji. W kolejności typowej wielkości uwalnianej energii, te typy reakcji to: jądrowe , chemiczne , elektrochemiczne i elektryczne .

Reakcje jądrowe zachodzą w gwiazdach i elektrowniach jądrowych, które czerpią energię z energii wiązania jąder. Organizmy wykorzystują reakcje chemiczne do pozyskiwania energii z pożywienia, a samochody do pozyskiwania energii z benzyny. Ciekłe węglowodory (paliwa takie jak benzyna, olej napędowy i nafta) są dziś najgęstszym znanym sposobem ekonomicznego magazynowania i transportu energii chemicznej na dużą skalę (1 kg oleju napędowego spala się tlenem zawartym w ≈15 kg powietrza). Reakcje elektrochemiczne są wykorzystywane przez większość urządzeń mobilnych, takich jak laptopy i telefony komórkowe, do uwalniania energii z baterii.

Rodzaje zawartości energii

Istnieje kilka różnych rodzajów zawartości energii. Jednym z nich jest teoretyczna całkowita ilość pracy termodynamicznej , którą można wyprowadzić z układu przy danej temperaturze i ciśnieniu narzuconym przez otoczenie. Nazywa się to egzergią . Innym jest teoretyczna ilość energii elektrycznej, którą można uzyskać z reagentów w temperaturze pokojowej i pod ciśnieniem atmosferycznym. Wynika to ze zmiany standardowej energii swobodnej Gibbsa . Ale jako źródło ciepła lub do zastosowania w silniku cieplnym , odpowiednią wielkością jest zmiana standardowej entalpii lub ciepło spalania .

Istnieją dwa rodzaje ciepła spalania:

  • Wyższa wartość (HHV), czyli ciepło spalania brutto, obejmuje całe ciepło uwalniane podczas schładzania produktów do temperatury pokojowej i kondensacji zawartej w nich pary wodnej.
  • Dolna wartość (LHV), czyli ciepło spalania netto, nie obejmuje ciepła, które mogłoby zostać uwolnione przez skraplanie pary wodnej i może nie obejmować ciepła uwolnionego podczas schładzania do temperatury pokojowej.

Wygodną tabelę HHV i LHV niektórych paliw można znaleźć w piśmiennictwie.

W magazynach energii i paliwach

Wybrany wykres gęstości energii

W zastosowaniach związanych z magazynowaniem energii gęstość energii wiąże energię w magazynie energii z objętością magazynu, np. zbiornika paliwa . Im wyższa gęstość energetyczna paliwa, tym więcej energii można zmagazynować lub przetransportować w tej samej objętości. Biorąc pod uwagę dużą gęstość energii benzyny, poszukiwanie alternatywnych nośników do magazynowania energii potrzebnej do zasilania samochodu, takich jak wodór lub akumulator, jest silnie ograniczone gęstością energii alternatywnego nośnika. Na przykład taka sama masa akumulatorów litowo-jonowych skutkowałaby samochodem o zaledwie 2% zasięgu jego benzynowego odpowiednika. Jeśli poświęcenie zasięgu jest niepożądane, konieczne staje się przewożenie znacznie większej ilości paliwa.

Gęstość energii paliwa na jednostkę masy nazywana jest energią właściwą tego paliwa. Ogólnie rzecz biorąc, silnik wykorzystujący to paliwo będzie generował mniej energii kinetycznej ze względu na nieefektywność i względy termodynamiczne - stąd jednostkowe zużycie paliwa przez silnik będzie zawsze większe niż szybkość wytwarzania energii kinetycznej ruchu.

Gęstość energii różni się od efektywności konwersji energii (wyjście netto na wsad) lub energii ucieleśnionej (koszty dostarczenia energii, ponieważ zbiory , rafinacja , dystrybucja i radzenie sobie z zanieczyszczeniami zużywają energię). Intensywne zużycie energii na dużą skalę ma wpływ na klimat , składowanie odpadów i konsekwencje dla środowiska .

Żadna pojedyncza metoda magazynowania energii nie może pochwalić się najlepszą mocą właściwą , energią właściwą i gęstością energii. Prawo Peukerta opisuje, w jaki sposób ilość użytecznej energii, którą można uzyskać (dla ogniwa kwasowo-ołowiowego), zależy od tego, jak szybko jest ono wyciągane.

Omówiono alternatywne opcje magazynowania energii w celu zwiększenia gęstości energii i skrócenia czasu ładowania.

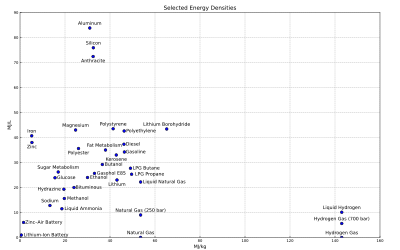
Powyższy rysunek przedstawia grawimetryczną i objętościową gęstość energii niektórych paliw i technologii magazynowania (zmodyfikowany z artykułu o benzynie ).

Niektóre wartości mogą nie być dokładne z powodu izomerów lub innych nieprawidłowości. Zobacz Wartość opałowa , aby zapoznać się z obszerną tabelą konkretnych energii ważnych paliw.

Generalnie wartości gęstości dla paliw chemicznych nie uwzględniają masy tlenu potrzebnego do spalania. Masy atomowe węgla i tlenu są podobne, podczas gdy wodór jest znacznie lżejszy. W ten sposób przedstawiono wartości dla tych paliw, dla których w praktyce powietrze zasysane byłoby tylko lokalnie do palnika. To wyjaśnia pozornie niższą gęstość energii materiałów zawierających własny utleniacz (takich jak proch strzelniczy i trotyl), w przypadku których masa utleniacza w efekcie zwiększa wagę i pochłania część energii spalania w celu dysocjacji i uwolnienia tlenu w celu kontynuowania reakcji . Wyjaśnia to również pewne pozorne anomalie, takie jak gęstość energii kanapki, która wydaje się być wyższa niż w przypadku laski dynamitu.

Lista gęstości energii materiałów

Zobacz też: Rozszerzona tabela referencyjna gęstości energii

Poniższe przeliczenia jednostek mogą być pomocne przy rozważaniu danych w tabelach: 3,6 MJ = 1 kW⋅h ≈ 1,34 hp⋅h . Ponieważ 1 J = 10 −6 MJ i 1 m 3 = 10 3 L, podziel dżul / m 3 przez 10 9 , aby otrzymać MJ / L = GJ/m 3 . Podziel MJ/L przez 3,6, aby otrzymać kW⋅h /L.

W reakcjach chemicznych (utlenianie)

Zobacz też: Wartość energetyczna biopaliwa i Wartość energetyczna żywności

O ile nie zaznaczono inaczej, wartości w poniższej tabeli są niższymi wartościami opałowymi dla doskonałego spalania , nie licząc masy ani objętości utleniacza. Gdy jest używany do wytwarzania energii elektrycznej w ogniwie paliwowym lub do wykonywania pracy , swobodna energia reakcji Gibbsa (Δ G ) wyznacza teoretyczną górną granicę. Jeśli wytwarzana H2O jest parą, to jest ona na niż mniejsza
ogół większa H2O jest ciekła, to jest na ogół dolne ciepło spalania, natomiast jeśli wytwarzana niż wyższe ciepło spalania. Ale w najbardziej odpowiednim przypadku wodoru Δ G wynosi 113 MJ/kg, jeśli wytwarzana jest para wodna, i 118 MJ/kg, jeśli wytwarzana jest woda w stanie ciekłym, przy czym obie wartości są mniejsze niż dolne ciepło spalania (120 MJ/kg).

Energia uwalniana w reakcjach chemicznych (utlenianie)
Materiał
Energia właściwa (MJ/kg)
Gęstość energii (MJ/l)
Energia właściwa ( W⋅h/kg )
Gęstość energii (W⋅h/L) 		Komentarz
Wodór, ciecz
141,86 ( HHV ) 119,93 ( LHV )
10.044 (HHV) 8.491 (LHV)
39 405,6 39 405,6 (HHV) 33 313,9 (LHV)
2790,0 (HHV) 2358,6 (LHV) 		Dane dotyczące energii obowiązują po podgrzaniu do 25°C.

Patrz uwaga powyżej dotycząca stosowania w ogniwach paliwowych.
Wodór, gaz (69 MPa, 25 °C)
141,86 (HHV) 119,93 (LHV)
5.323 (HHV) 4.500 (LHV)
39 405,6 39 405,6 (HHV) 33 313,9 (LHV)
1478,6 (HHV) 1250,0 (LHV) 		Data z tego samego odniesienia, co dla ciekłego wodoru.

Zbiorniki wysokociśnieniowe ważą znacznie więcej niż wodór, który mogą pomieścić. Wodór może stanowić około 5,7% całkowitej masy, co daje zaledwie 6,8 MJ na kg masy całkowitej dla LHV.

Patrz uwaga powyżej dotycząca stosowania w ogniwach paliwowych.
Wodór, gaz (1 atm lub 101,3 kPa, 25 ° C)
141,86 (HHV) 119,93 (LHV)
0,01188 (HHV) 0,01005 (LHV)
39 405,6 39 405,6 (HHV) 33 313,9 (LHV)
3,3 (HHV) 2,8 (LHV)
Diboran 78,2 88,4 21722,2 24600
Beryl 67,6 125,1 18777,8 34750,0
Borowodorek litu 65,2 43,4 18111,1 12055,6
Bor 58,9 137,8 16361,1 38277,8
Metan (101,3 kPa, 15 °C) 55,6 0,0378 15444,5 10,5
LNG (NG przy -160 ° C) 53,6 22.2 14888,9 6166,7
CNG (NG skompresowany do 25 MPa ≈ 3600 psi ) 53,6 9 14888,9 2500,0
Gazu ziemnego 53,6 0,0364 14888,9 10.1
LPG propan 49,6 25.3 13777,8 7027,8
LPG butan 49.1 27,7 13638,9 7694,5
Benzyna (benzyna) 46,4 34.2 12888,9 9500,0
Tworzywo polipropylenowe 46,4 41,7 12888,9 11583,3
Tworzywo polietylenowe 46,3 42,6 12861,1 11833,3
Olej opałowy do mieszkań 46,2 37,3 12833,3 10361,1
Olej napędowy 45,6 38,6 12666,7 10722,2
benzyna 100 LL 44,0 31,59 12222,2 8775,0
Paliwo do silników odrzutowych (np. nafta ) 43 35 11944,4 9722,2 Silnik samolotu
Gasohol E10 (obj. 10% etanolu 90% benzyny) 43,54 33.18 12094,5 9216,7
Lit 43.1 23.0 11 972,2 6388,9
biodiesel (olej roślinny) 42.20 33 11722,2 9166,7
DMF (2,5-dimetylofuran) 42 37,8 11666,7 10500,0 [ wymagane wyjaśnienie ]
Parafina 42 37,8 11700 10500
Ropa naftowa ( tona ekwiwalentu ropy naftowej ) 41.868 37 11630 10278
Plastik polistyrenowy 41,4 43,5 11.500,0 12083,3
Tłuszcz 38 35 10555,6 9722,2 Metabolizm w organizmie człowieka (wydajność 22%)
Butanol 36,6 29.2 10166,7 8111,1
Gasohol E85 (85% etanolu 15% objętościowo benzyny) 33.1 25,65 [ potrzebne źródło ] 9194,5 7125,0
Grafit 32,7 72,9 9083,3 20250,0
Węgiel , antracyt 26–33 34–43 7222,2–9166,7 9444,5–11 944,5 Liczby przedstawiają doskonałe spalanie nie licząc utleniacza, ale sprawność konwersji na energię elektryczną wynosi ≈36%
Krzem 32,6 75,9 9056 21080 Patrz Tabela 1
Aluminium 31.0 83,8 8611,1 23277,8
Etanol 30 24 8333,3 6666,7
DME
31,7 (HHV) 28,4 (LHV)
21,24 (HHV) 19,03 (LHV)
8805,6 8805,6 (HHV) 7888,9 (LHV)
5900,0 (HHV) 5286,1 (LHV)
Tworzywo poliestrowe 26.0 35,6 7222,2 9888,9
Magnez 24,7 43,0 6861,1 11 944,5
Fosfor (biały) 24.30 44.30 6750 12310
Węgiel , bitum 24–35 26–49 6666,7–9722,2 7222,2–13611,1
PET (zanieczyszczony) 23,5 < ~32,4 6527,8 < ~9000
Metanol 19.7 15.6 5472,2 4333,3
Tytan 19.74 88,93 5480 24700 spalone do dwutlenku tytanu
Hydrazyna (spalana do N 2 + H 2 O) 19,5 19.3 5416,7 5361,1
Ciekły amoniak (spalany do N 2 + H 2 O) 18.6 11,5 5166,7 3194,5
Potas 18.6 16,5 5160 4600 spalony do sucha tlenek potasu
PVC ( niewłaściwe spalanie toksyczne ) 18.0 25.2 5000,0 7000,0 [ wymagane wyjaśnienie ]
Drewno 18.0 5000,0
Brykiet torfowy 17.7 4916,7
Cukry, węglowodany i białko 17 26,2 ( dekstroza ) 4722,2 7277,8 Metabolizm w organizmie człowieka (wydajność 22%) [ potrzebne źródło ]
Wapń 15.9 24.6 4416,7 6833,3 [ potrzebne źródło ]
Glukoza 15.55 23,9 4319,5 6638,9
Suche łajno krowie i łajno wielbłądzie 15,5 4305,6
Węgiel , lignit 10–20 2777,8–5555,6 [ potrzebne źródło ]
Sód 13.3 12.8 3694,5 3555,6 spalone do mokrego wodorotlenku sodu
Torf 12.8 3555,6
nitrometan 11.3 12.85 3138,9 3570
Mangan 9.46 68.2 2630 18 900 spalone do dwutlenku manganu
Siarka 9.23 19.11 2563,9 5308,3 spalony na dwutlenek siarki
Sód 9.1 8.8 2527,8 2444,5 spalony do sucha tlenek sodu
Akumulator, akumulator litowo-powietrzny 9.0 2500,0 Kontrolowane wyładowanie elektryczne
Odpady z gospodarstw domowych 8.0 2222,2
Cynk 5.3 38,0 1472,2 10555,6
Żelazo 5.2 40,68 1444,5 11300,0 spalony do tlenku żelaza(III).
Tworzywo teflonowe 5.1 11.2 1416,7 3111,1 spalanie toksyczne, ale trudnopalne
Żelazo 4.9 38.2 1361,1 10611,1 spalony do tlenku żelaza(II).
Proch strzelniczy 4,7–11,3 5,9–12,9 1600–3580
TNT 4.184 6,92 1162 1920
Bar 3,99 14.0 1110 3890 spalony do dwutlenku baru
ANFO 3.7 1027,8

W reakcjach jądrowych

Energia uwalniana w reakcjach jądrowych
Materiał
Energia właściwa (MJ/kg)
Gęstość energii (MJ/l)
Energia właściwa ( W⋅h/kg )
Gęstość energii (W⋅h/L) 		Komentarz
Antymateria 89 875 517 874 ≈ 90 PJ/kg Zależy od gęstości formy antymaterii 24 965 421 631 578 ≈ 25 TW⋅h/kg Zależy od gęstości formy antymaterii Anihilacja, licząc zarówno zużytą masę antymaterii, jak i masę zwykłej materii
Wodór (fuzja) 639 780 320, ale co najmniej 2% z tego jest tracone przez neutrina . Zależy od warunków 177 716 755 600 Zależy od warunków Reakcja 4H→ 4 He
Deuter (synteza jądrowa)
571 182 758 Zależy od warunków 158 661 876 600 Zależy od warunków Proponowany schemat fuzji dla D+D→ 4 He, poprzez połączenie D+D→T+H, T+D→ 4 He+n, n+H→D i D+D→ 3 He+n, 3 He+D→ 4 He+H, n+H→D
Deuter + tryt (fuzja) 337 387 388 Zależy od warunków 93 718 718 800 Zależy od warunków
D + T → 4 He + n W trakcie opracowywania.
Deuterek litu-6 (fuzja) 268 848 415 Zależy od warunków 74 680 115 100 Zależy od warunków
6 LiD → 2 4 Używany w broni.
Pluton-239 83 610 000 1 300 000 000–1 700 000 000 (w zależności od fazy krystalograficznej ) 23 222 915 000 370 000 000 000–460 000 000 000 (w zależności od fazy krystalograficznej ) Ciepło wytwarzane w reaktorze rozszczepienia
Pluton-239 31 000 000 490 000 000–620 000 000 (w zależności od fazy krystalograficznej ) 8 700 000 000 140 000 000 000–170 000 000 000 (w zależności od fazy krystalograficznej ) Energia elektryczna produkowana w reaktorze rozszczepienia
Uran 80 620 000 1 539 842 000 22 394 000 000 Ciepło wytwarzane w reaktorze powielającym
Tor 79 420 000 929 214 000 22 061 000 000 Ciepło wytwarzane w reaktorze powielającym (eksperyment)
Pluton-238 2 239 000 43 277 631 621 900 000 Radioizotopowy generator termoelektryczny . Ciepło jest wytwarzane tylko w ilości 0,57 W/g.

Inne mechanizmy uwalniania

Energia uwalniana w wyniku reakcji elektrochemicznych lub w inny sposób
Materiał
Energia właściwa (MJ/kg)
Gęstość energii (MJ/l)
Energia właściwa ( W⋅h/kg )
Gęstość energii (W⋅h/L) 		Komentarz
Bateria cynkowo-powietrzna 1,59 6.02 441,7 1672,2 Kontrolowane wyładowanie elektryczne
Krzem (zmiana fazy) 1.790 4.5 500 1285 Energia zmagazynowana poprzez zmianę fazy stałej w ciekłą krzemu
Ciekły azot 0,77 0,62 213,9 172,2 Maksymalna praca odwracalna przy 77,4 K ze zbiornikiem 300 K
Akumulator sodowo-siarkowy 0,54–0,86 150–240
Sprężone powietrze pod ciśnieniem 30 MPa 0,5 0,2 138,9 55,6 Energia potencjalna
Utajone ciepło topnienia lodu (termiczne) 0,334 0,334 93.1 93.1
Bateria litowo-metalowa 1.8 4.32 500 1200 Kontrolowane wyładowanie elektryczne
Bateria litowo-jonowa 0,36–0,875 0,9–2,63 100.00–243.06 250,00–730,56 Kontrolowane wyładowanie elektryczne
Akumulator litowo-jonowy z anodami z nanoprzewodów krzemowych 1.566 4.32 435 1200 Kontrolowane wyładowanie elektryczne
Koło zamachowe 0,36–0,5 5.3 Energia kinetyczna
Bateria alkaliczna 0,48 1.3 Kontrolowane wyładowanie elektryczne
Akumulator niklowo-wodorkowy 0,41 0,504–1,46 Kontrolowane wyładowanie elektryczne
Akumulator kwasowo-ołowiowy 0,17 0,56 Kontrolowane wyładowanie elektryczne
Superkondensator ( EDLC ) 0,01–0,030 0,006–0,06 do 8,57 Kontrolowane wyładowanie elektryczne
Woda na wysokości tamy 100 m 0,000981 0,000978 0,272 0,272 Liczby przedstawiają energię potencjalną, ale sprawność konwersji na energię elektryczną wynosi 85–90%
Kondensator elektrolityczny 0,00001–0,0002 0,00001–0,001 Kontrolowane wyładowanie elektryczne

W deformacji materiału

Zdolność magazynowania energii mechanicznej lub sprężystość materiału Hooke'a , gdy jest on odkształcony do punktu zniszczenia, można obliczyć, obliczając wytrzymałość na rozciąganie pomnożoną przez maksymalne wydłużenie, dzieląc przez dwa. Maksymalne wydłużenie materiału Hooke'a można obliczyć, dzieląc sztywność tego materiału przez jego wytrzymałość na rozciąganie. W poniższej tabeli wymieniono te wartości obliczone przy użyciu modułu Younga jako miary sztywności:

Pojemności energii mechanicznej
Materiał Gęstość energii według masy

(J/kg)

 Sprężystość : Gęstość energii objętościowo

(J L)

 Gęstość

(kg/L)

 Moduł Younga

(GPa)

 Granica plastyczności przy rozciąganiu

(MPa)
Gumka recepturka 1651–6605 2200–8900 1.35
Stal, ASTM A228 (wydajność, średnica 1 mm) 1440–1770 11 200–13 800 7.80 210 2170–2410
Acetale 908 754 0,831 2.8 65 (ostateczny)
Nylon-6 233–1870 253–2030 1.084 2–4 45–90 (ostateczny)
Miedź Beryl 25-1/2 HT (wydajność) 684 5720 8.36 131 1224
Poliwęglany 433–615 520–740 1.2 2.6 52–62 (ostateczny)
tworzywa ABS 241–534 258–571 1.07 1,4–3,1 40 (ostateczny)
Akryl 1530 3.2 70 (ostateczny)
Aluminium 7077-T8 (wydajność) 399 1120 2.81 71,0 400
Stal nierdzewna , 301-H (wydajność) 301 2410 8.0 193 965
Aluminium 6061-T6 (wydajność przy 24°C) 205 553 2,70 68,9 276
Epoksydowa żywica 113–1810 2–3 26–85 (ostateczny)
Drewno daglezji 158-200 96 0,481–0,609 13 50 (kompresja)
Stal, miękka AISI 1018 42,4 334 7,87 205 370 (440 ostatecznych)
Aluminium (niestopowe) 32,5 87,7 2,70 69 110 (ostateczny)
Sosna (amerykańska wschodnia biel, zginanie ) 31,8–32,8 11,1–11,5 0,350 8,30–8,56 (zginanie) 41,4 (giętkość)
Mosiądz 28,6–36,5 250–306 8,4–8,73 102–125 250 (ostateczny)
Miedź 23.1 207 8.93 117 220 (ostateczny)
Szkło 5,56–10,0 13,9–25,0 2.5 50–90 50 (kompresja)

W bateriach

Pojemność energetyczna baterii
Urządzenie pamięci masowej
Zawartość energii ( dżul )
Zawartość energii ( W⋅h ) 		Rodzaj energii
Typowa masa (g)
Typowe wymiary (średnica × wysokość w mm) 		Typowa objętość (ml)
Gęstość energii objętościowo (MJ/L)
Gęstość energii na masę (MJ/kg)
Bateria alkaliczna AA 9360 2.6 Elektrochemiczny 24 14,2 × 50 7,92 1.18 0,39
Bateria alkaliczna typu C 34416 9.5 Elektrochemiczny 65 26 × 46 24.42 1.41 0,53
NiMH AA 9072 2.5 Elektrochemiczny 26 14,2 × 50 7,92 1.15 0,35
NiMH C 19440 5.4 Elektrochemiczny 82 26 × 46 24.42 0,80 0,24
Akumulator litowo-jonowy 18650 28 800–46 800 10,5–13 Elektrochemiczny 44–49 18 × 65 16.54 1,74–2,83 0,59–1,06

Źródła energii jądrowej

Zdecydowanie największym źródłem energii jest sama materia. Ta energia, E = mc 2 , gdzie m = ρV , ρ to masa na jednostkę objętości, V to objętość samej masy, a c to prędkość światła. Energia ta może jednak zostać uwolniona tylko w procesach rozszczepienia jądrowego (0,1%), syntezy jądrowej (1%) lub anihilacji części lub całości materii w objętości V w wyniku zderzeń materia- antymateria (100%) . [ potrzebne źródło ] Reakcje jądrowe nie mogą być realizowane przez reakcje chemiczne, takie jak spalanie. Chociaż można osiągnąć większe gęstości materii, gęstość gwiazdy neutronowej byłaby zbliżona do najgęstszego możliwego układu zdolnego do anihilacji materii i antymaterii. Czarna dziura , chociaż gęstsza niż gwiazda neutronowa, nie ma równoważnej formy antycząstki, ale oferuje ten sam 100% współczynnik konwersji masy na energię w postaci promieniowania Hawkinga. W przypadku stosunkowo małych czarnych dziur (mniejszych niż obiekty astronomiczne) moc wyjściowa byłaby ogromna.

Źródłami energii o największej gęstości poza antymaterią są synteza jądrowa i rozszczepienie . Fuzja obejmuje energię ze słońca, która będzie dostępna przez miliardy lat (w postaci światła słonecznego), ale jak dotąd (2021) trwała energii z syntezy jądrowej nadal jest nieuchwytna.

Energia z rozszczepienia uranu i toru w elektrowniach jądrowych będzie dostępna jeszcze przez wiele dziesięcioleci, a nawet stuleci, ze względu na obfitość pierwiastków na ziemi, choć pełny potencjał tego źródła można zrealizować jedynie za pomocą reaktorów powielających, które oprócz z reaktora BN-600 , dotychczas nieużywany komercyjnie. Węgiel , gaz i ropa naftowa są obecnie głównymi źródłami energii w USA, ale mają znacznie niższą gęstość energii. Spalanie lokalnych z biomasy zaspokaja potrzeby energetyczne gospodarstw domowych ( kominki do gotowania , lampy naftowe itp.) na całym świecie.

Moc cieplna reaktorów jądrowych

Gęstość energii cieplnej zawartej w rdzeniu reaktora lekkowodnego ( PWR lub BWR ) o typowej mocy 1 GWe (1000 MW energii elektrycznej odpowiadającej ≈3000 MW energii cieplnej) mieści się w zakresie od 10 do 100 MW energii cieplnej na metr sześcienny wodę chłodzącą w zależności od rozpatrywanej lokalizacji w systemie (sam rdzeń (≈30 m 3 ), zbiornik ciśnieniowy reaktora (≈50 m 3 ) lub cały obieg pierwotny (≈300 m 3 )). Oznacza to znaczną gęstość energii, która w każdych okolicznościach wymaga ciągłego przepływu wody z dużą prędkością, aby móc odprowadzać ciepło z rdzenia, nawet po awaryjnym wyłączeniu reaktora. Niezdolność do schłodzenia rdzeni trzech reaktorów z wrzącą wodą (BWR) w Fukushimie w 2011 roku po tsunami i związana z tym utrata zewnętrznego zasilania elektrycznego i źródła chłodu była przyczyną stopienia trzech rdzeni w ciągu zaledwie kilku godzin , mimo że trzy reaktory zostały prawidłowo wyłączone tuż po trzęsieniu ziemi w Tōhoku . Ta niezwykle wysoka gęstość mocy odróżnia elektrownie jądrowe (EJ) od wszelkich elektrowni cieplnych (spalających węgiel, paliwo lub gaz) lub jakichkolwiek zakładów chemicznych i wyjaśnia dużą redundancję wymaganą do stałej kontroli reaktywności neutronów i usuwania resztkowego ciepła z rdzenia elektrowni jądrowych.

Gęstość energii pól elektrycznych i magnetycznych

Główny artykuł: Gęstość energii promieniowania

Pola elektryczne i magnetyczne magazynują energię. (Objętościowa) gęstość energii jest określona przez

gdzie E to pole elektryczne , B to pole magnetyczne , a ε i µ to odpowiednio przenikalność i przepuszczalność otoczenia. Rozwiązaniem będzie (w jednostkach SI) w dżulach na metr sześcienny. W kontekście magnetohydrodynamiki , fizyki płynów przewodzących, gęstość energii magnetycznej zachowuje się jak dodatkowe ciśnienie , które dodaje się do ciśnienia gazu w plazmie .

W idealnych (liniowych i niedyspersyjnych) substancjach gęstość energii (w jednostkach SI) wynosi

gdzie D jest polem przemieszczenia elektrycznego , a H jest polem magnesującym .

W przypadku braku pól magnetycznych, wykorzystując zależności Fröhlicha , można również rozszerzyć te równania na dielektryki anizotropowe i nieliniowe , a także obliczyć skorelowaną energię swobodną Helmholtza i gęstość entropii .

laser impulsowy uderza w powierzchnię, ekspozycję na promieniowanie , tj. energię zdeponowaną na jednostkę powierzchni, można nazwać gęstością energii lub fluencją.

Zobacz też

przypisy

Dalsza lektura

  •   Wszechświat inflacyjny: poszukiwanie nowej teorii pochodzenia kosmicznego autorstwa Alana H. Gutha (1998) ISBN 0-201-32840-2
  •   Inflacja kosmologiczna i struktura na dużą skalę, Andrew R. Liddle, David H. Lyth (2000) ISBN 0-521-57598-2
  • Richard Becker, „Pola elektromagnetyczne i interakcje”, Dover Publications Inc., 1964

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Energy_density&oldid=1140309379 ”